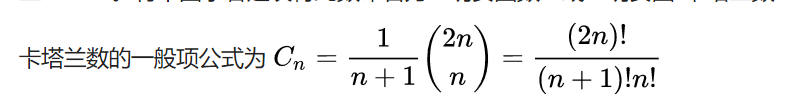数据结构1800刷题😁错题集
序号标题为解答,引用为题目和答案
- 由栈的先进后出原则
入栈:1——n-i+1——n
输出:P1——Pi——Pn
出栈:n——n-i+1——1
若已知一个栈的入栈序列是1,2,3,⋯ ,n,其输出序列为p1,p2,p3,⋯, pN,若pN 是n,则
pi 是( D ) 。
A. i B. n-i C. n-i+1 D. 不确定
- 栈的图解,注意初始顶指针

若一个栈以向量V[1…n] 存储,初始栈顶指针top 为n+1,则下面x 进栈的正确操作是
( C )。
A. top:=top+1; V [top]:=x B. V [top]:=x; top:=top+1
C. top:=top-1; V [top]:=x D. V [top]:=x; top:=top-1
- 共享栈 图解

若栈采用顺序存储方式存储, 现两栈共享空间V[1…m] ,top[i] 代表第i 个栈( i =1,2) 栈顶,
栈1 的底在v[1] ,栈2 的底在V[m] ,则栈满的条件是( B )。
A. |top[2]-top[1]|=0 B. top[1]+1=top[2] C. top[1]+top[2]=m D. top[1]=top[2]
- 思路:题目给出的是中缀表达式,先将表达式用树的形式来显示,再后序遍历。

表达式a*(b+c)-d 的后缀表达式是( B )。【南京理工大学2001 一、2(1.5 分)】
A.abcd*± B. abc+d- C. abc+d- D. -+*abcd
- 分为两个栈,分别存储,数值和运算符。(应用牛客网解答)
链接:https://www.nowcoder.com/questionTerminal/3a42f706132940218436b70cc9d32227
来源:牛客网
一、准备两个栈:操作数栈s1,运算符栈s2。
二、从【左至右】扫描表达式:32^(4+22-63)-5;
遵循的原则是: 遇到操作数入s1栈;若遇到运算符c,则需要与s2的栈顶 字符c2进行优先级比较;
《1》若c > c2,则c入栈;
《2》若c < c2,则c2退栈,并将s1栈顶的两个元素退栈与操作符一起运算,将结果入s1栈;
(1)操作数3,入栈s1;
(2)运算符,入栈s2;
(3)操作数2,入栈s1;
(4)运算符^ ,入栈s2;(理由是:^的优先级 高于 的优先级)
(5)运算符(,直接入s2;
(6)操作数4,入栈s1;
(7)运算符+,入栈s2;(理由是:( 后面的运算符直接入栈)
(8)…数2,入栈s1;
(9)…符,入栈s2;(理由是:的优先级 高于 +的优先级)
(10)…数2,入栈s1;
(11)…符 -,(由于 -的优先级低于)s2的栈顶字符 * 出栈,并完成22=4的运算,将结果4存入s1中;—s1:3,2,4,4;
(由于 -的优先级低于+)s2的栈顶字符+出栈,并完成4+4=8的运算,将结果8存入s1中;—s1:3,2,8;
此时,- 成为了(后的运算符,则直接入栈s2;—s2:^(-;
(12)…数6;
表达式3* 2^(4+22-63)-5 求值过程中当扫描到6 时,对象栈和算符栈为( ),其中^
为乘幂。
A. 3,2,4,1,1 ; (^(+-
B. 3,2,8 ; (^-
C. 3,2,4,2,2; (^(-
D. 3,2,8 ; (*^(-
- 1> 当有多于一个节点时,链表表示的队列的删除操作只需要修改头指针即可,将头指针定义为head=head.next 此时不需要修改尾指针;
2> 当队列只有一个节点时,该节点既是头又是尾,如果head==tail 则需要修改尾指针将队列置空。
用链接方式存储的队列,在进行删除运算时( D )。
A. 仅修改头指针
B. 仅修改尾指针
C. 头、尾指针都要修改
D. 头、尾指针可能
都要修改
- 同上
用不带头结点的单链表存储队列时,其队头指针指向队头结点,其队尾指针指向队尾结点,则在进行删除操作时( D )。【北京理工大学2001 六、3(2 分)】
A.仅修改队头指针
B. 仅修改队尾指针
C. 队头、队尾指针都要修改
D. 队头,队尾指针都可能要修改
- 在顺序队列中,当队尾指针已经到数组的上界,不能再有入队操作,但其实数组中还有空位置,这就叫做==“假溢出”,解决假溢出的途径----采用循环队列==。
假设以数组A[m] 存放循环队列的元素,其头尾指针分别为front 和rear,则当前队列中的
元素个数为( A )。【北京工商大学2001 一、2(3 分)】
A.(rear-front+m)%m
B.rear-front+1
C.(front-rear+m)%m
D.(rear-front)%m
- 注意是 m+1 个内存空间
循环队列存储在数组 A[0…m] 中,则入队时的操作为 ( D )。
A. rear=rear+1
B. rear=(rear+1) mod (m-1)
C. rear=(rear+1) mod m
D. rear=(rear+1)mod(m+1)
最大容量为 n 的循环队列,队尾指针是 rear,队头是 front,则队空的条件是 ( B )。
A. (rear+1) MOD n=front
B. rear=front
C.rear+1=front
D. (rear-l) MOD n=front
- 循环队列的相关条件和公式:
1.队空条件:rear==front
2.队满条件:(rear+1) %QueueSIze==front,其中QueueSize为循环队列的最大长度
3.计算队列长度:(rear-front+QueueSize)%QueueSize
4.入队:(rear+1)%QueueSize
5.出队:(front+1)%QueueSize
- 栈的规律,根据给出的选项,从左到右,逐个查看当前这个元素,往后面比他顺序小的元素,是否按照逆序的序列拍好。
依次读入数据元素序列 {a,b,c, d,e,f, g}进栈 ,每进一个元素,机器可要求下一个元素进栈或弹栈, 如此进行, 则栈空时弹出的元素构成的序列是以下哪些序列? (A D)
A.{d ,e,c,f,b,g,a} B. {f ,e,g,d,a,c,b}
C. {e,f,d,g,b, c,a} D. {c ,d,b,e,f,a, g}
- 两个栈共用静态存储空间,栈底相接,但总的空间大小有限 也存在溢出问题
两个栈共用静态存储空间,对头使用也存在空间溢出问题。 ( V )
- 两个栈,bottom分别为线性表的两端
当两个栈共享一存储区时, 栈利用一维数组 stack(1,n)表示,两栈顶指针为 top[1] 与 top[2] ,则当栈 1 空时, top[1] 为0,栈 2 空时 ,top[2] 为n+1,栈满时为 top[1] + 1 = top[2]。
- 如果多于两个栈时,还是采用顺序存储,则一个满了另外栈空间虽然有空,但是必须要移动栈中元素才能使用别的浪费的空间,这样算法的效率就不高了,此时不如直接采用链接存储好了
多个栈共存时,最好用 链式存储作为存储结构
- 假溢出-rear超出了队列所在分配空间,但是前面还有空白的空间

循环队列的引入,目的是为了克服 假溢出时候,避免移动大量元素
区分循环队列的满与空,只有两种方法,它们是 设标记和牺牲一个存储单元。