Java破解9X9数独小游戏

背景

最近刷到LeetCode上这道有趣的题目，想起了初中时候对数独的热爱，不禁感慨万分，原来这个用编程不到1m就能出结果，害我以前还浪费了这么多时间去研究。

效果

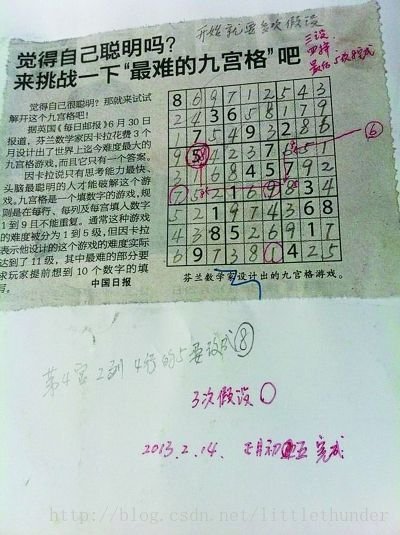
据说这是最难的数独题目【点此链接进入】，就拿它开刀吧

初始局面:
8........
..36.....
.7..9.2..
.5...7...
....457..
...1...3.
..1....68
..85...1.
.9....4..开始求解时刻:
2021/06/12 11:59:45答案:
812753649
943682175
675491283
154237896
369845721
287169534
521974368
438526917
796318452结束求解时刻:
2021/06/12 11:59:45耗时:33ms

源代码

一、算法代码：Solution.java

public class Solution {/*** 行*/final int ROW=9;/*** 列*/final int COL=9;/*** 第i行是否填充了value*/boolean [][]row=new boolean[ROW][COL];/*** 第i列是否填充了value*/boolean [][]col=new boolean[ROW][COL];/*** 第i个小九宫是否填充了value*/boolean [][]mid=new boolean[ROW][COL];/*** 数独*/char[][] board;/*** 是否已经得出答案*/boolean solve=false;/*** 求解数独* @param board 数独*/public void solveSudoku(char[][] board) {//初始化三个布尔数组for(int i=0;i<ROW;i++) {for(int j=0;j<COL;j++) {if(board[i][j]=='.') {continue;}else {row[i][board[i][j]-'0'-1]=true;col[j][board[i][j]-'0'-1]=true;mid[i/3*3+j/3][board[i][j]-'0'-1]=true;}}}this.board=board;dfs(0,0);}/*** 深度优先* @param i* @param j*/public void dfs(int i,int j) {//已经解决则不再计算if(solve) {return;}//已经解决的条件if(i>=ROW||j>=COL) {solve=true;return;}//不是空格则无法填数if(board[i][j]!='.') {if(j==COL-1) {dfs(i+1,0);}else {dfs(i,j+1);}return;}//尝试填入1~9，只有没出现过的才能填入，且填入后立即更新已填的布尔数组，事后变回原样for(int number=1;number<=9;number++) {//它是不合法的就跳过if(row[i][number-1]||col[j][number-1]||mid[i/3*3+j/3][number-1]) {continue;//否则尝试填入}else {//尝试填入board[i][j]=(char)(number+48);//更新已填布尔数组row[i][number-1]=true;col[j][number-1]=true;mid[i/3*3+j/3][number-1]=true;//向下一个元素出发//行末处，跳到下一行if(j==COL-1) {dfs(i+1,0);//未到行末，跳到此行下一个元素}else {dfs(i,j+1);}//尝试结束，若没有出结果则重置原样if(solve) {return;}else {board[i][j]='.';row[i][number-1]=false;col[j][number-1]=false;mid[i/3*3+j/3][number-1]=false;}}}}
}

二、测试代码Main.java

import java.text.SimpleDateFormat;
import java.util.Date;public class Main {public static void main(String[] args) {// TODO Auto-generated method stubchar[][]board=new char[9][9];//String value="530070000\n600195000\n098000060\n800060003\n400803001\n700020006\n060000280\n000419005\n000080079";String value="800000000\n003600000\n070090200\n050007000\n000045700\n000100030\n001000068\n008500010\n090000400";String []rows=value.split("\n");for(int i=0;i<rows.length;i++) {for(int j=0;j<rows[i].length();j++) {board[i][j]=rows[i].charAt(j);if(board[i][j]=='0') {board[i][j]='.';}}}System.out.println("初始局面:");display(board);SimpleDateFormat sdf=new SimpleDateFormat("yyyy/MM/dd HH:mm:ss");Date start=new Date();System.out.println();System.out.println("开始求解时刻:");System.out.println(sdf.format(start));long s=System.currentTimeMillis();Solution solution=new Solution();solution.solveSudoku(board);System.out.println();System.out.println("答案:");display(board);System.out.println();Date end=new Date();System.out.println("结束求解时刻:");System.out.println(sdf.format(end));System.out.println();long e=System.currentTimeMillis();System.out.println("耗时:"+(e-s)+"ms");}public static void display(char[][] board) {for(int i=0;i<9;i++) {for(int j=0;j<9;j++) {System.out.print(board[i][j]);}System.out.println();}}
}

算法思路

让电脑模拟人的思维，根据数独规则，每行、列、小九宫内数字1-9能且仅能出现一次。根据此规则，我们可以定义三个哈希数组来存储这三种情况。

布尔数组row，给它九行九列，让row[i][number]来表示i+1行是否出现过number+1【注意计算机的数组下标从零开始，当然你可以根据习惯舍弃第0行列而从1开始】。

布尔数组col，给它九行九列，让col[i][number]来表示i+1列是否出现过number+1【注意计算机的数组下标从零开始，当然你可以根据习惯舍弃第0行列而从1开始】。

布尔数组mid，给它九行九列，让mid[i][number]来表示i+1个小九宫是否出现过number+1【注意计算机的数组下标从零开始，当然你可以根据习惯舍弃第0行列而从1开始】。

拿到题目时我们先根据给出的信息，填充好我们设定的三个布尔数组。紧接着就是我们万能破解尝试类游戏的模板之一：深度优先搜索，为了将程序写的简单，我们使用递归写法。为了同学们这里少采坑，我总结了一下四条经验【我们从第1行开始，一行一行地去尝试填数。函数原型：f(i,j)，表示当前尝试的元素是i+1行、j+1列的】。

1.设置哨兵[布尔类型],作为求解结束的标志，即得出一个结果时，通知递归函数跳出。

2.当尝试的行列超出了9，说明求出结果了，哨兵至true，跳出递归。

3.当前元素已经填过了，那就跳过它，尝试下一个元素

4.当前元素没有填过，将可能的值填入，并更新表示已填的那三个布尔数组，尝试下一个元素。如果尝试完成后问题解决了，就退出递归函数，否则就重置刚刚的状态：包括局面和三个布尔数组。