注:未经同意不要转载。
上学期简单的做了一个数独程序,实现了一些功能,想简单的为大家提供的思路。
为了避免某些情况出现,具体代码暂时先不发了,有不太懂的地方可以评论提问啊。
下面是我的具体报告:
一,实验目的
用C语言实现数独
二,实验要求
(1)实验基本要求
编写代码实现数独的部分功能,包括将当前数独状态输出到屏幕上、插入一个数、修改一个数、检查当前数独是否成立。
(2)加分项
1, 能够判断数独是否可解
2, 能够给出当前状态下,数独的下一步的提示
3, 能够进行题目的初始化,即能够让计算机给出一个最终只有唯一解的数独题目
三,实验内容
- 实现了基本功能,可以通过文件读取数独;把数独的当前状态和修改一个数判断数独是否成立。
- 实现了加分项,判断数独是否可解;给出提示;计算机生成数独题目。
- 增加的功能,实现了生成的难度选择;输入了一个数独模板,可以生成特定形状的数独;可以玩一个数独游戏。
- 将功能串联起来,使之成为一个完整的程序。
四,算法基本原理
(1)解出数独(最基本的思路)
解出一个数独是该程序最基本。我采用的是最简单的方式,暴力解数独。大概就是,对于空缺处从左到右,从上到下填。填入的时侯对于一个空位,先试着填入1,然后判断这个数是否符合要求,符合要求的话,先填入,如果不符合要求,就将这个数加一再试着填,再不符合要求就再加一,直到已经加到10时,说明此时前面填写的是有问题的。就返回上一个空位,对上一个空位填入的数加一。并以此类推。最终填完最后一个空位时,数独就已经解出了。
遇到的问题:暴力解的思路比较简单,运算量也不是太大。开始的时候遇到的最大的问题是如何返回上一个空位。解决的思路有两种,一种是对应的空位用指针链表,这种思路涉及到链表结构体,而且必须按照顺序进行操作;另外一种思路是利用新定义的两个数组按顺序的把空位对应的位置存储起来,这样的话每次返回上一个空位只需要将新定义的数组下标减一就能实现,而且容易理解。因此,我最终采用了第二种方法。
(这是找空位的函数)
(其中b数组存放的是空位的行,c数组存放的是空位的列,m代表的是空位的总个数)

(实际上解数独的函数)
(2) 判断可解
判断可解的思路是在解数独的基础上的。判断的时候,思路是解这个数独,如果这个数独填空位的时候在不断的返回,最终导致第一个空位加到了10,此时程序依然会放回,就返回到了第0个空位(假设有第0个空位)。那么说明计算机已经把所有空位可能的情况都填过了,但是没有找到最终的解,说明此数独是无解数独。那么空位返回到了第0个,那么就可判断出这个数独是不可解的。
所以最终解数独和判断可解写成。
(3)找出一个数独的多解
由于暴力解数独的时候是按照顺序来填的,那么我们想找下一个解,仅需要把上一个解的最后一个空位的候选位加一,让程序继续解数独的操作(这一步是用goto语句实现的)。直到最后返回到了第0个空位,所有可能的解都已经被输出了。
(多解的思路就是将解数独和判断数独是否可解的思路结合起来)。
(返回的值e-1直接代表解的个数)
(4)生成数独
生成数独的思路也有两种。一种是随机生成一板数独,然后挖空;另一种是先选好空,用随机数生成的方法,按要求填上不是空缺的地方。两种思路生成好之后都要判断数独是否有单解(这里用到了多解的思路,为了减少运算量,特意改了一下解多解的情况,没有必要找出所有的多解,只要已经查出有两个解时,就重新生成)。如果不是唯一解的话,就再进行生成,直到有唯一解为止。考虑到效率问题,最终才用了第一种。
关于函数作用的注释:
Judge()函数:用于判断这个数独是否已经填完,用于实现玩一个函数判断书否结束。
Findshu()函数:用于判断生成的数独的已经填入数的位置的数目,用于控制生成的难度。
Printf_shudu()函数:用于打印数独答案。
Printf_shudu()函数:用于打印目前数独以及生成的数独。
Findvoid()函数:用于找出输入的数独的空位,方便解数独时返回上一位。
Judge()函数:用于判断这个数能否填在这个位置,主要用于解数独。
Duojie_solve()函数:判断一个数独解的情况,仅适用于生成一个数独时所用。
Duojie_solve()函数:输出一个数独解的情况。
Solve()函数:最简单的找出数独的一个解。
Creat_shudu()函数:生成一个特定模板的数独。
Creat_shudu1()函数:生成数独的思路1。
Creat_shudu2()函数:生成数独思路2。
Play_shudu()函数:实现玩一个数独游戏的功能。
Judge_shudukejie()函数:实现更改一个数,判断是否还是可解的功能。
五,实现的功能
- 基本要求
1,打开一个数独文件。利用基本的文件操作就能完成。在网络上找了1000道数独题,以txt的形式保存下来,可以直接读取。
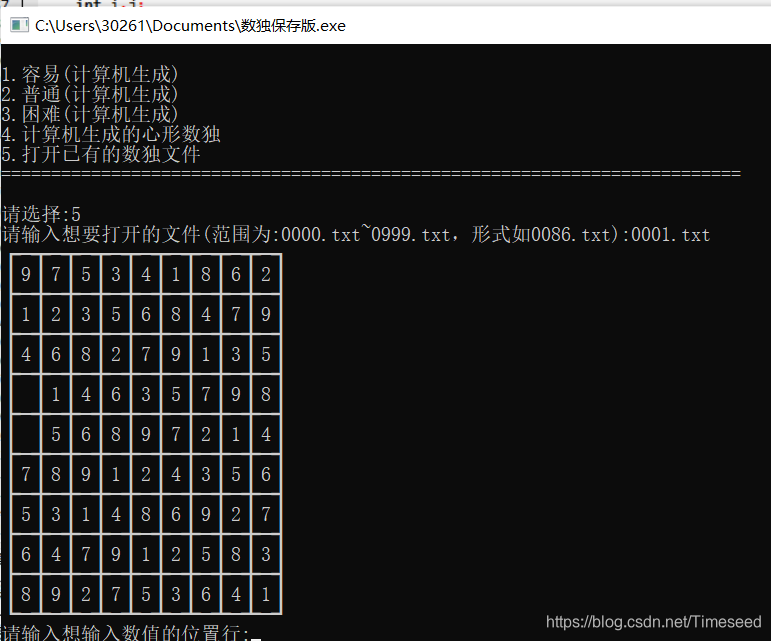
(界面和打开一个文件的结果)
2,包括将当前数独状态输出到屏幕上、插入一个数、修改一个数、检查当前数独是否成立。
实现这个要求仅需对某个确定的位置进行更改,然后把判断数独解的情况即可

(2) 判断数独是否可解和给出提示
判断数独是否可解用到了原理2。
运行结果:

(输入一个数独)

(有唯一解的情况)
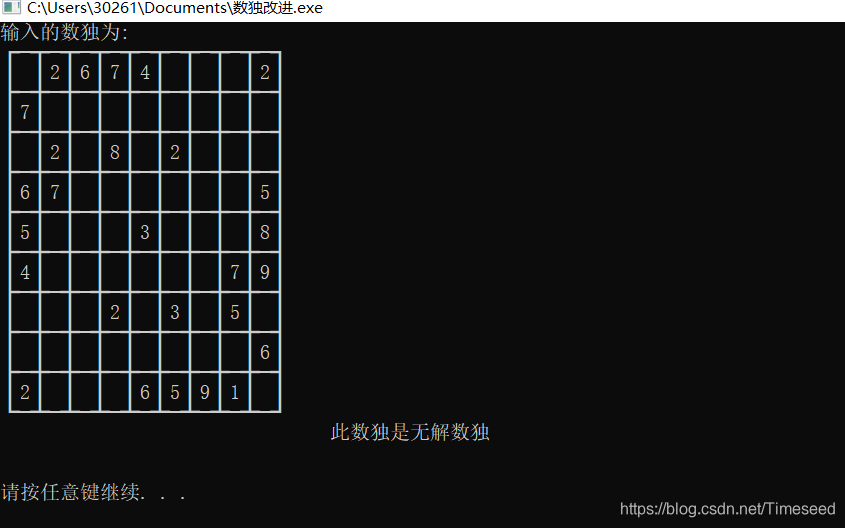
(无解的情况)

(多解的情况)
更改一个数判断是否还是可解的:
这里就是简单的把更改后的数独进行多解的判断。


给出下一步提示:由于采用的是暴力解法,并不能从逻辑上给出下一步的解,但是给出某个位置解的情况还是容易实现的。
-
-
- 生成唯一解的题目以及控制生成的难度
-
思路的比较:第一种思路,先选好空,用随机数生成的方法,按要求填上不是空缺的地方,这种情况发生了由于会产生较多的无解情况。实际效率是比较慢的,耗时比较长,生成的情况。(这个思路也保存到了最终的代码里,只是没有实际采用,这个函数是creat_shudu1)。
运行的结果:

(第一种思路生成的数独以及其对应的唯一解)
当然第一种思路可以指定模板进行生成,我就录入了一个爱心形的模板,利用同样的思路生成了一个数独。
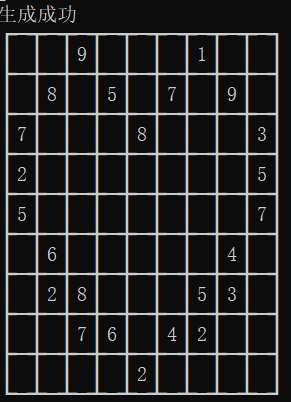
(生成的特定形状的数独)
第二种思路是生成一板数独答案,然后挖空生成数独,显然这种情况不会出现无解的情况,而挖的空数目不多又会让多解的情况减少(甚至不出现)。使效率大大提高。
运行结果:

(生成的数独以及其对应的解)
采取了两个思路,第二种思路生成的数独,用时较短而且比较容易控制难度。这里只考虑最简单的,仅根据空的多少来简单的判定难度,因此仅仅需要控制挖空的多少即可控制生成数独的难度。
(第二种思路生成的唯一解数独及其对应的解)
控制生成的难度
这里简单的定义了难度,已有数为35为困难,45为普通难度,60为简单的难度

(生成的简单难度数独以及对应的解)

(生成的普通难度数独)

(生成的困难难度)
(4)玩一个数独
既然都数独的基本功能都实现了,我就稍微的把这几个功能整合了一下,形成了一个基本的小程序。把以上的基本功能串联了起来。完善了细节。如把计算机生成数独放在了玩一个数独游戏的功能中。
运行结果:
 (选择玩一个数独的界面)
(选择玩一个数独的界面)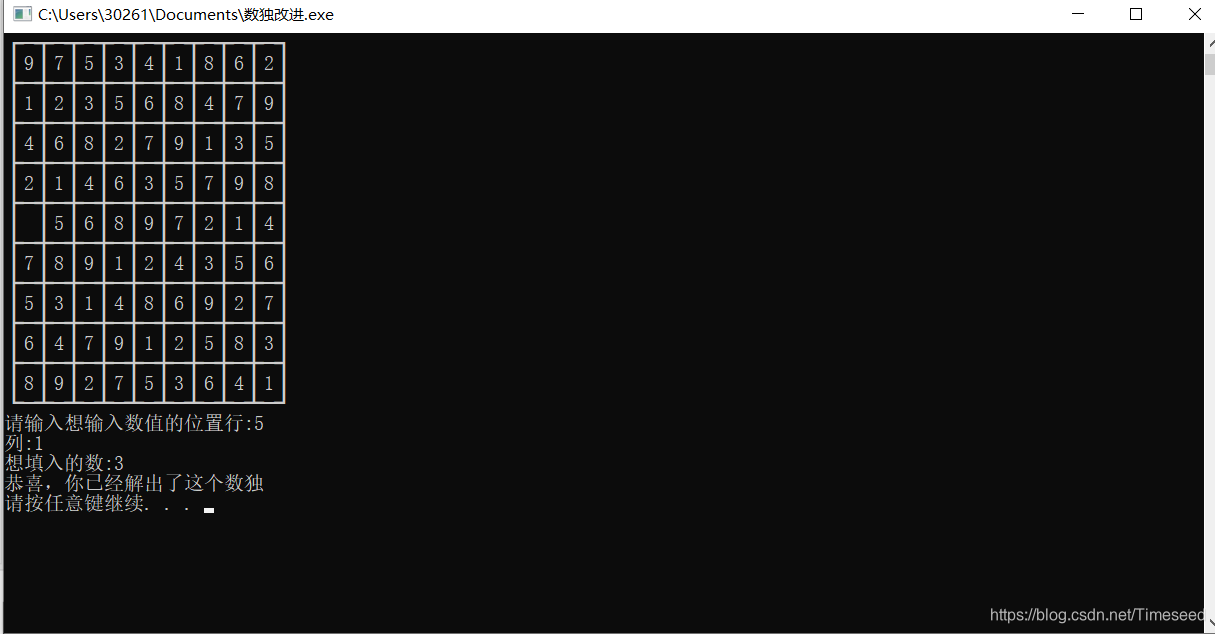
(解完一个数独得情况)