拓扑排序：神经网络

题目链接

神经网络

题目大意

在兰兰的模型中，神经网络就是一张有向图，图中的节点称为神经元，而且两个神经元之间至多有一条边相连，下图是一个神经元的例子：
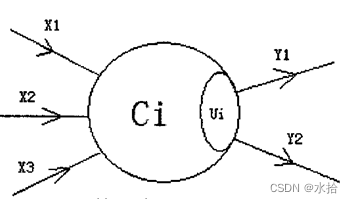
在这里插入图片描述
图中， $X_1—X_3$ 是信息输入渠道， $Y_1－Y_2$ 是信息输出渠道， $C_i$ 表示神经元目前的状态， $U_i$ 是阈值，可视为神经元的一个内在参数。

神经元按一定的顺序排列，构成整个神经网络。在兰兰的模型之中，神经网络中的神经无分为几层；称为输入层、输出层，和若干个中间层。每层神经元只向下一层的神经元输出信息，只从上一层神经元接受信息。下图是一个简单的三层神经网络的例子。
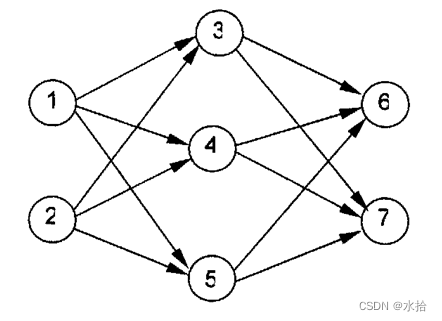
在这里插入图片描述
兰兰规定， $C_i$ 服从公式：（其中 $n$ 是网络中所有神经元的数目）

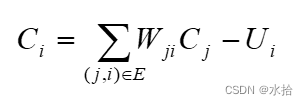
公式中的 $W_{ji}$ （可能为负值）表示连接 jj 号神经元和 ii 号神经元的边的权值。当 $C_i$ 大于 0 时，该神经元处于兴奋状态，否则就处于平静状态。当神经元处于兴奋状态时，下一秒它会向其他神经元传送信号，信号的强度为 $C_i$ 。如此．在输入层神经元被激发之后，整个网络系统就在信息传输的推动下进行运作。现在，给定一个神经网络，及当前输入层神经元的状态（ $C_i$ ），要求你的程序运算出最后网络输出层的状态。

输入格式

输入第一行是两个整数 n $\leq n \leq 20）$ 和 p。接下来 n 行，每行两个整数，第 i＋1行是神经元 i 最初状态和其阈值（ $U_i$ ），非输入层的神经元开始时状态必然为 0。再下面 $P$ 行，每行由两个整数 $i, j$ 及一个整数 $W_{ij}$ ,表示连接神经元 ii、jj 的边权值为 $W_{ij}$ 。

输出格式

输出若干行，每行有两个整数，分别对应一个神经元的编号，及其最后的状态，两个整数间以空格分隔。仅输出最后状态非零的输出层神经元状态，并且按照编号由小到大顺序输出！

若输出层的神经元最后状态均为 $0$ ，则输出 $N ULL$ 。

解题思路

权值的传递过程如何

拓扑排序

拓扑排序：对一个有向无环图G进行拓扑排序，是将G中所有顶点排成一个线性序列，使得图中任意一对顶点u和v，若边 $< u, v >\in E (G)$ ，则u在线性序列中出现在v之前。通常，这样的线性序列称为满足拓扑次序(Topological Order)的序列，简称拓扑序列。
简单的说，由某个集合上的一个偏序得到该集合上的一个全序
总览：从入度为0的点开始遍历，一直到出度为0的点。
思路分步：
1、首先输入时确定是否为输入层，非输入层可以直接在这里减去U。
2、根据公式，要求一个点的权值C，就要求出所有的C[j]*W[i,j]。
3、所有的节点的权值是从他的上一个节点推过来的，根据公式求权值。通过拓扑排序，C[i]的值简单地累加。

AC Code

Python3

# -*- coding: utf-8 -*-
# @Author : BYW-yuwei
# @Software: python3.8.6
N = 110
P = 100001
edges =[0 for _ in range(P)]
head = [0 for _ in range(N)]
U = [0 for _ in range(N)]
C = [0 for _ in range(N)]
in_node = [0 for _ in range(N)]
out_node = [0 for _ in range(N)]
num_edges = 1def add_edge(u,v,w):global num_edgesedges[num_edges] = [head[u],v,w] head[u] = num_edgesnum_edges += 1n,p = map(int,input().split())
for i in range(n):C[i],U[i] = map(int,input().split())if C[i] == 0:C[i] -= U[i]
for i in range(p):u,v,w = map(int,input().split())add_edge(u,v,w)in_node[v]+=1out_node[u]+=1def topologicalSort():queue = []for i in  range(1,n+1):#从1编号if in_node[i]==0:queue.append(i)while queue:u = queue.pop(0)i = head[u]while i:v = edges[i][1]in_node[v]=in_node[v]-1if in_node[v] ==0:queue.append(v)if C[u-1]>0:C[v-1]+= edges[i][2]*C[u-1]i = edges[i][0]def solve():topologicalSort()tag = 1for i in range(n):if C[i] > 0 and out_node[i+1]==0:print(i+1,C[i])tag = 0if tag:print("NULL")
solve()