简介:

   A*算法是一个种静态路网中求解最短路径最有效的直接搜索方法，是一种启发式搜索

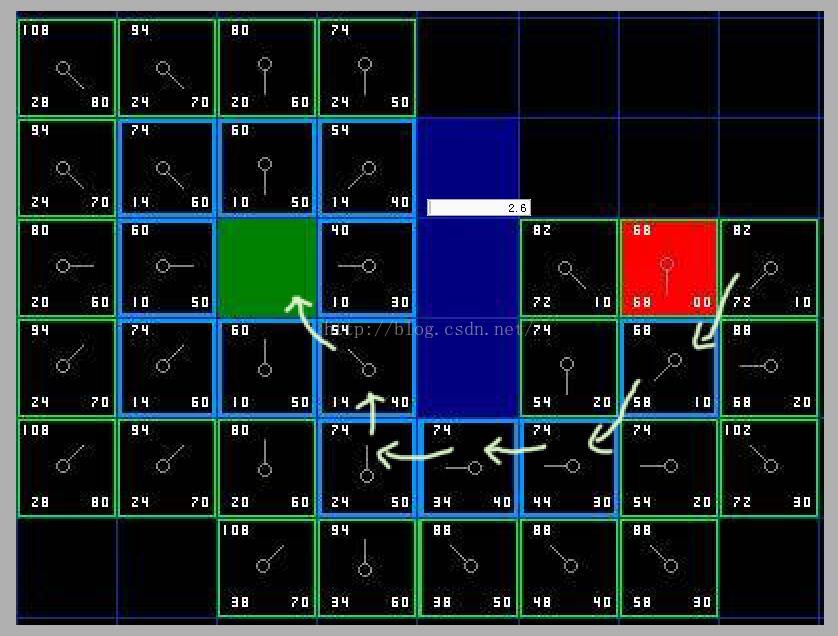
地图:

 

大致思路:

首先要有一个开启列表和一个关闭列表

开启列表中用来存放所有可能走的点（可以使用优先队列）

关闭列表中存放所有走过的点

1：先将起点加入开启列表中

2：在开启列表中找到F值最低的点（F值的计算下面讲）

3：将该点加入到关闭列表中，并从开始列表中移除

4：遍历该点的周围8格

{

      如果不能走，或者在关闭列表中，则continue

      否则判断是否在开启列表中，如果在就继续比较该点当前的G值和原来的G值，并更新状态，更新该点的父节点

      如果不在开启列表，则计算GHF值，设置父节点

      判断是否找到最终点，如果找到退出循环，否则重复循环

}

5:当开启列表不为空，或者没有找到最终点时，一直循环234，当开启列表为空时，则表示没有找到点

 

GHF值的计算：

f(n)：从起点到终点的估计代价值，f(n)=g(n)+h(n)

g(n)：从起点到节点的实际代价值，g(n)=当前代价值+父节点的g值，方便计算，将距离都*10，直边：10，斜边：14

h(n)：从节点到达终点的估计代价值，一般用2种计算方式，欧几里和曼哈顿

欧几里：斜边长度（2点间距离公式）

曼哈顿：x的距离差+y的距离差

 

代码:

void AStar::Astar()  
{  Point begin;  begin.x = hero.x;  begin.y = hero.y;  begin.f = begin.g = begin.h = 0;  begin.next = nullptr;  OpenList.push_back(begin);                                                              //将起始点放入关闭列表中  while (!OpenList.empty())  {  OpenList.sort(AStar());                                                             //将开启列表按f值从小到大排序  CloseList.push_back(OpenList.front());                                              //将开启列表的f值最小的点，加入关闭列表中  OpenList.pop_front();                                                               //将该点从开启列表中删除  for (int i = 0; i < 8; i++)  {  Point Temp;  Temp.x = CloseList.back().x + nextX[i];   Temp.y = CloseList.back().y + nextY[i];  if (map[Temp.x][Temp.y] == 1 || true == Find(Temp.x, Temp.y))                   //该点不为墙，或者该点不在关闭列表中  continue;  if (false == Judge(i))                                                          //判断该点能不能走  continue;  Temp.g = CloseList.back().g + (int)sqrt(abs(nextX[i]) + abs(nextY[i])) * 10;    //计算点的g值  Temp.h = (abs(target.x - Temp.x) + abs(target.y - Temp.y)) * 10;                //计算点的h值  Temp.f = Temp.g + Temp.h;                                                       //计算点的f值  Temp.next = &CloseList.back();                                                  //设置父节点  if (false == FindOpen(Temp))  {  OpenList.push_back(Temp);                                                   //将该点加入开启列表中  }   if (true == Find(target.x, target.y))                                           //找到目标点，结束函数  {  return;  }  }  }  
}