a*自动寻路算法详解

这篇博文是在其他博客基础上加工的，主要原因是感觉原博客举得例子不太好，很多细节感觉没有描述。

A*算法主要是在父节点更新那个地方很容易误解，但是父节点的更新又是A*算法的核心，因为遍历到目标节点之后就是根据父节点回溯返回找到的路径的。

开始：

一只探路猫

让我们想象一下，有一款游戏，游戏中一只猫想要找到获取骨头的路线。

“为什么会有一只猫想要骨头？！”你可能会这么想。在本游戏中，这是一只狡猾的猫，他想捡起骨头给狗，以防止被咬死！:]

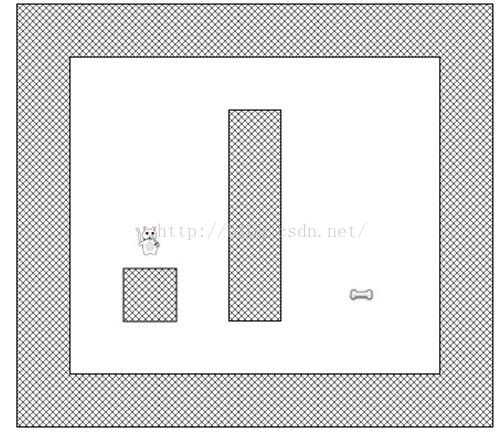
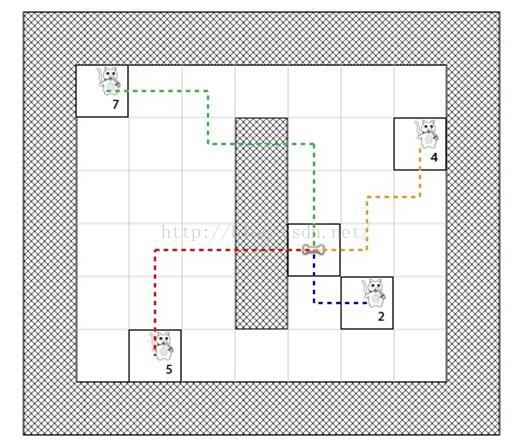
现在想像一下下图中的猫想找到到达骨头的最短路径：

不幸的是，猫不能直接从它当前的位置走到骨头的位置，因为有面墙挡住了去路，而且它在游戏中不是一只幽灵猫！

游戏中的猫同样懒惰，它总是想找到最短路径，这样当他回家看望它的女朋友时不会太累:-)

但是我们如何编写一个算法计算出猫要选择的那条路径呢？A星算法拯救了我们！

简化搜索区域

寻路的第一步是简化成容易控制的搜索区域。

怎么处理要根据游戏来决定了。例如，我们可以将搜索区域划分成像素点，但是这样的划分粒度对于我们这款基于方块的游戏来说太高了（没必要）。

作为代替，我们使用方块（一个正方形）作为寻路算法的单元。其他的形状类型也是可能的（比如三角形或者六边形），但是正方形是最简单并且最适合我们需求的。

像那样去划分，我们的搜索区域可以简单的用一个地图大小的二维数组去表示。所以如果是25*25方块大小的地图，我们的搜索区域将会是一个有625个正方形的数组。如果我们把地图划分成像素点，搜索区域就是一个有640，000个正方形的数组了（一个方块是32*32像素）！

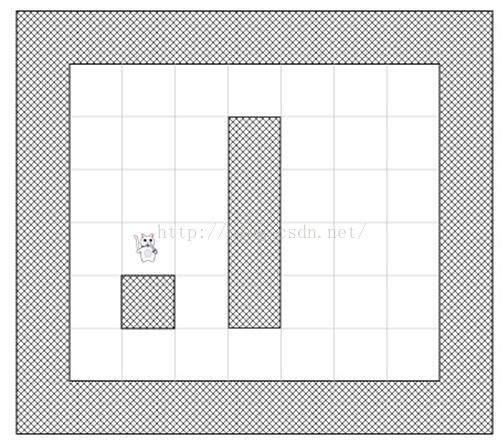
现在让我们基于目前的区域，把区域划分成多个方块来代表搜索空间（在这个简单的例子中，7*6个方块 = 42个方块）：

Open和Closed列表

既然我们创建了一个简单的搜索区域，我们来讨论下A星算法的工作原理吧。

除了懒惰之外，我们的猫没有好的记忆力，所以它需要两个列表：

一个记录下所有被考虑来寻找最短路径的方块（称为open 列表）
一个记录下不会再被考虑的方块（成为closed列表）

猫首先在closed列表中添加当前位置（我们把这个开始点称为点 “A”）。然后，把所有与它当前位置相邻的可通行小方块添加到open列表中。

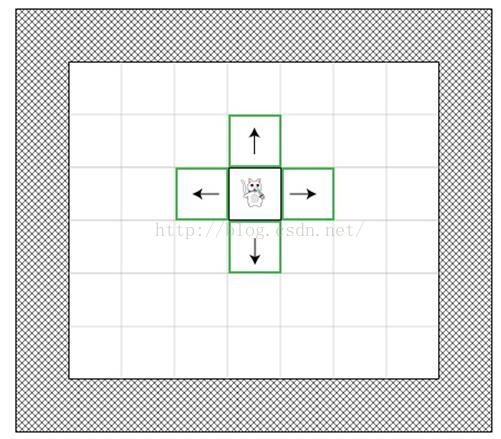
下图是猫在某一位置时的情景（绿色代表open列表）:

现在猫需要判断在这些选项中，哪项才是最短路径，但是它要如何去选择呢？

在A星寻路算法中，通过给每一个方块一个和值，该值被称为路径增量。让我们看下它的工作原理！

路径增量

我们将会给每个方块一个G+H和值：

· G是从开始点A到当前方块的移动量。所以从开始点A到相邻小方块的移动量为1，该值会随着离开始点越来越远而增大。

· H是从当前方块到目标点（我们把它称为点B，代表骨头！）的移动量估算值。这个常被称为探视，因为我们不确定移动量是多少 – 仅仅是一个估算值。

你也许会对“移动量”感兴趣。在游戏中，这个概念很简单 –仅仅是方块的数量。

然而，在游戏中你可以对这个值做调整。例如：

· 如果你允许对角线移动，你可以针对对角线移动把移动量调得大一点。

· 如果你有不同的地形，你可以将相应的移动量调整得大一点 –例如针对一块沼泽，水，或者猫女海报:-)

这就是大概的意思 –现在让我们详细分析下如何计算出G和H值。

关于G值

G是从开始点A到达当前方块的移动量（在本游戏中是指方块的数目）。

为了计算出G的值，我们需要从它的前继（上一个方块）获取，然后加1。所以，每个方块的G值代表了从点A到该方块所形成路径的总移动量。

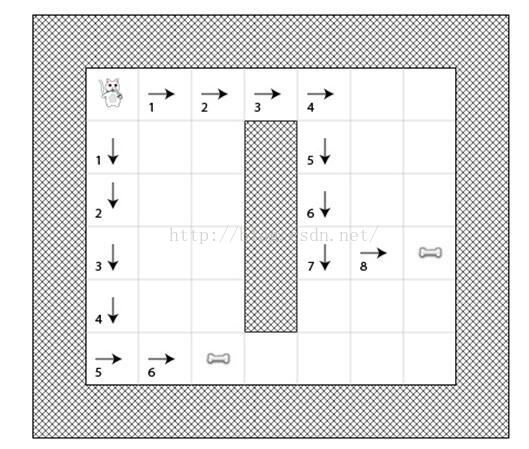
例如，下图展示了两条到达不同骨头的路径，每个方块都标有它的G值：

关于H值

H值是从当前方块到终点的移动量估算值（在本游戏中是指方块的数目）。

移动量估算值离真实值越接近，最终的路径会更加精确。如果估算值停止作用，很可能生成出来的路径不会是最短的（但是它可能是接近的）。这个题目相对复杂，所以我们不会再本教程中讲解，但是我在教程的末尾提供了一个网络链接，对它做了很好的解释。

为了让它更简单，我们将使用“曼哈顿距离方法”（也叫“曼哈顿长”或者“城市街区距离”），它只是计算出距离点B，剩下的水平和垂直的方块数量，略去了障碍物或者不同陆地类型的数量。

例如，下图展示了使用“城市街区距离”，从不同的开始点到终点，去估算H的值（黑色字）：

A星算法

既然你知道如何计算每个方块的和值（我们将它称为F，等于G+H), 我们来看下A星算法的原理。

猫会重复以下步骤来找到最短路径：

将方块添加到open列表中，该列表有最小的和值。且将这个方块称为S吧。
将S从open列表移除，然后添加S到closed列表中。
对于与S相邻的每一块可通行的方块T：

· 如果T在closed列表中：不管它。

· 如果T不在open列表中：添加它然后计算出它的和值。

· 如果T已经在open列表中：当我们使用当前生成的路径到达那里时，检查F和值是否更小。如果是，更新它的和值和它的前继。

如果你对它的工作原理还有点疑惑，不用担心 –我们会用例子一步步介绍它的原理！:]

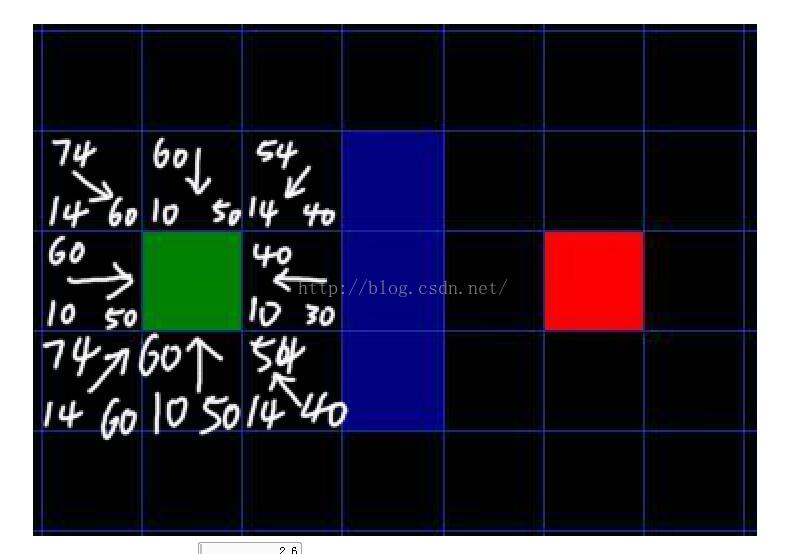
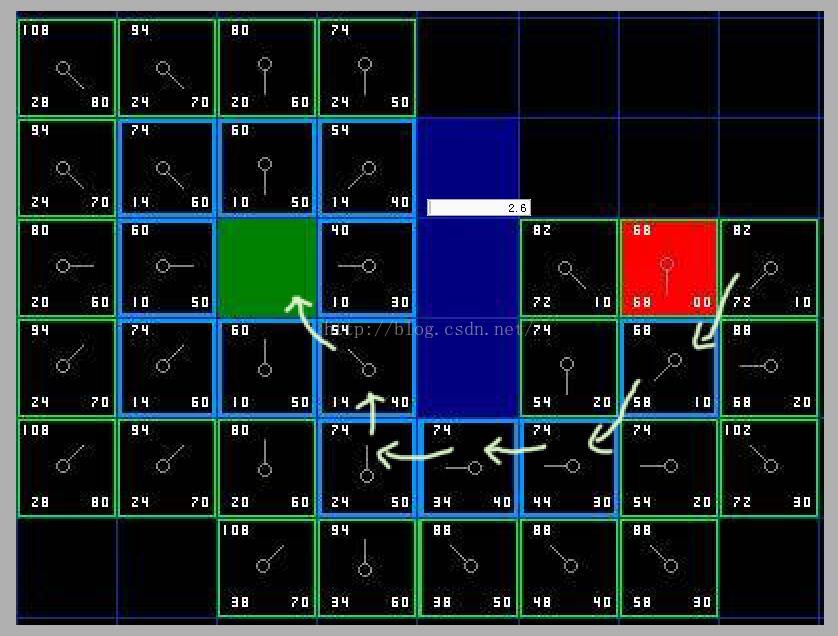
如下图方格中左下角：G，方格右下角：H，左上角：F

F=G+H (其实这个公式不用理解也行，主要是为了方便计算的)

上图是第一步：计算起点周围邻域的代价，跨越一条边是10，对角是14,

把周围节点的G和H计算出来之后，计算F（就是G+H）。然后再赋予父节点，其实可以想象初始的时候所有节点的F都是无穷大的，为什么要这么理解呢，主要是节点的父指针就是根据F来变化的。

因为一开始都是无穷大，所以邻域节点的F计算出来之后都要比无穷大小，那么，这些节点的父指针就指向当前的起始节点。如上图所示。因为此时这几个邻域节点都没有在open列表中，于是就把这8个点加到open队列中，并且把当前节点也就是起始节点放到close中（也就是下次不再考虑了）。

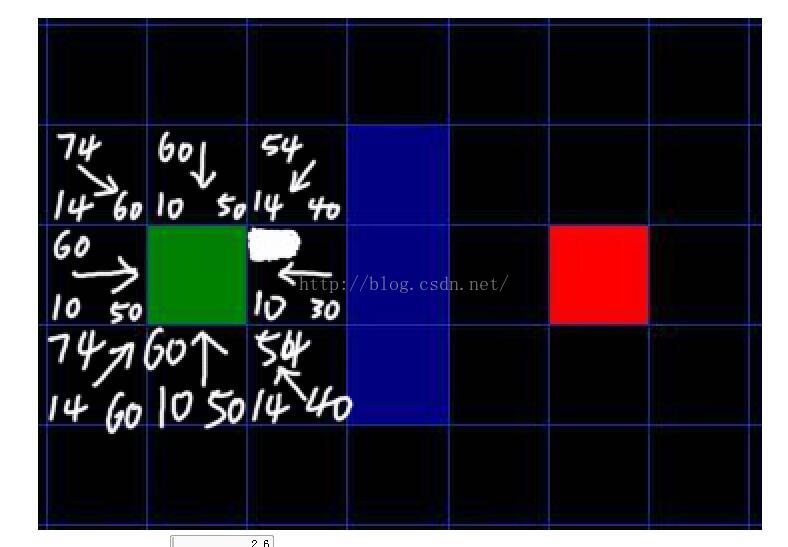
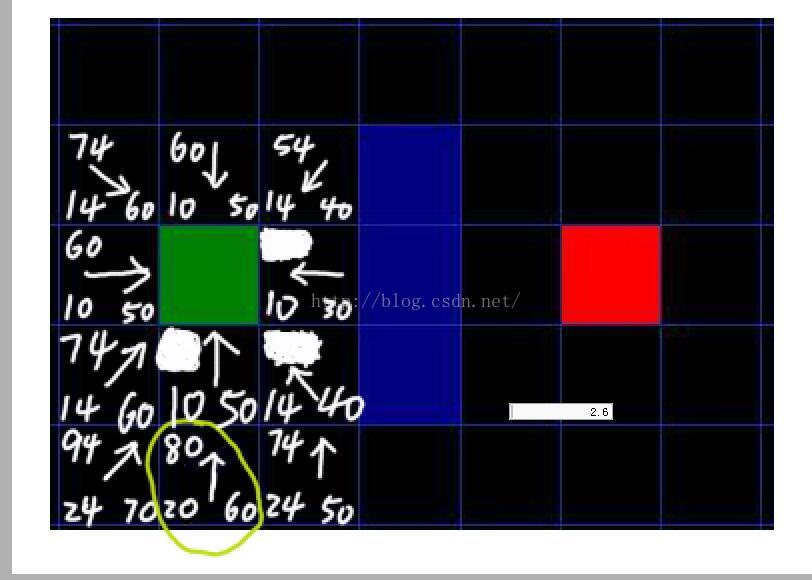
第二步：从open队列中选择F最小的那个节点，此时可能有F相同的（这种情况就随便选个，不影响最短路径长度），我们选择40的那个，于是，把F=40的这个节点作为当前节点，如下图所示：（此时我们把40抹去了，因为之后会把这个节点放到close队列中，close队列中的点都是不考虑的，也是为了描述方便，我们要的只是指针方向）

关键：

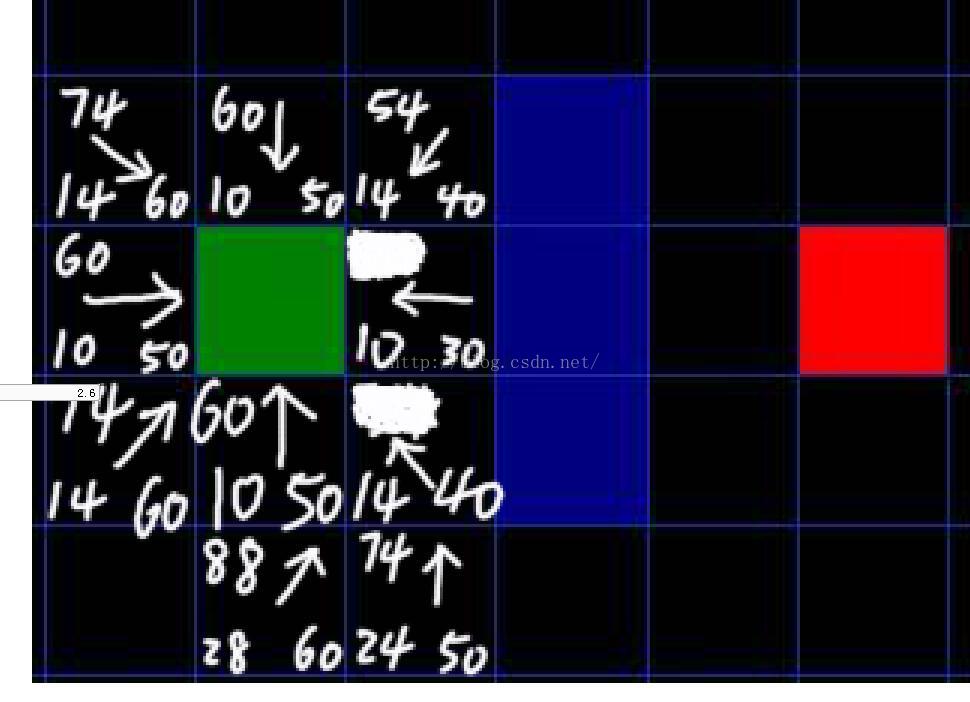
第三步：把40的那个节点周围8邻域的节点计算完F后，放到open队列中，注意，此时障碍物的节点和已经放入close队列的节点不放，那么此时没有新节点加入进来，由于把涂抹了的那个节点当成当前节点，所以需要重新计算它的8邻域节点的G值和F值，（也就是它的上方那个，坐上方节点，下方节点，左下方节点，一个4个），此时G值的计算是这样的：比如计算上方那个（54 14 40），由于从原点到当前节点的G为10，从当前节点到上方节点的G值为10，所以10+10=20（也就是所到上方节点需要先从原点到这个点，然后在从这个点到上面那个点），但是新计算的G=20<14(节点原来的G值)，所以上方节点的指针方向不变，（如果计算出来小于原来的值，那么就把上方节点的指针指向当前这个节点了）！！

同样计算剩下的三个节点的G值，发现都大于原来的G值，所以节点指针方向没有做任何改变。

于是把当前节点放到close对列中，再从open队列中找F值最小的节点。（此时队列中有7个节点）

于是把54那个节点（起始节点的右下方那个）当成当前节点，计算周围8邻域的G值和F值。但是障碍物下方的那个点不能加入计算，因为从当前节点到障碍物下方那个节点必须穿透墙角了！

同样赋予节点父指针以及更新8邻域的G值和F值。