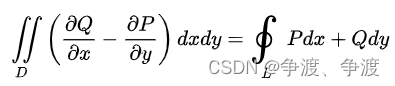泊松方程是静电场问题的基础，下面我们以此方法为基础

自由空间中的泊松方程

可以证明这个方程的解为

用相同的方法，这个解记作格林函数
在自由空间下，任意泊松方程的

解可以写为

          

这就是静电场的叠加原理

如果不是自由空间，这个公式是不成立的，因为有除了空间内电荷，还有感应电荷分布。

这个公式的完整形式是

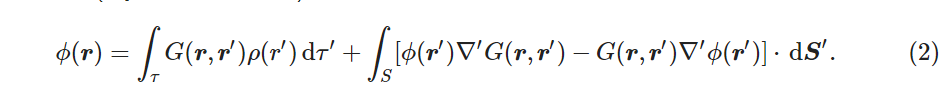
第一项就是之前算的源电荷的积分所产生的影响。第二项为边界上的电势和电荷的影响。

假设给定一个闭合区域，闭合区域内无电荷分布，闭合区域接地，那么不论区域外面的情况如何，区域内都没有影响,见(2)

在有边界情况下静电场问题，通常有两类边界条件

1.给定边界电势，再求格林函数的时候要求再边界处G(r,r')=0,那么(2)只有前两项的部分，由镜像法，可以求出半无穷平面边界和球外边界的格林函数，由此可以解决静电场问题

例子1：半无限大平面上方圆形环，带电势为V0，求上半平面电势能。

由(2)等式，只需计算格林函数在边界平面的法向导数，既可以解决这个问题。

例子2:  球面带电导体，在上半球面的电压为V，在下半球面的电压为-V，求球外的电势。

这个例子是利用球外的格林函数变为球坐标表示，利用(2)的第二公式就能求解。

2.第二类边界条件

给定边界电势的梯度（对应电荷密度），用(2)势求解还需要知道在边界上的平均电荷密度。要求格林函数满足的条件于前面不同。所以求解起来比较困难，这里就不讲了

思考以及练习，求解球内边界条件的格林函数，并利用球内边界的格林函数解决第一类边值问题。