目录
- 前言
- Akima简介
- Akima优势
- 算法的代码实现
- python版
- C++ 版
- 代码解析1
- 代码解析2
- 代码解析3
- C版
- 实验对比
前言
鉴于“长沙等你”网站上Akima算法文章大部分要VIP观看或者下载,即使是付费也有质量不佳,浪费Money也浪费时间。
笔者根据查到的资料分享给大家。
Akima简介
Akima 拟合算法是 Hiroshi Akima 于 1970 年开发的一种插值和曲线拟合方法。Akima 插值算法对于构造通过给定数据点集的平滑曲线特别有用。它广泛应用于各个领域,包括计算机图形学、图像处理和数值分析。
Akima 拟合算法不同于传统的插值方法,例如线性或多项式插值,它提供了更稳健和视觉上令人愉悦的数据表示。它侧重于最大限度地减少在其他插值技术中经常观察到的振荡或摆动。此算法的工作原理是将给定数据分成小区间,然后将分段三次曲线拟合到每个区间。该方法确保生成的曲线在区间边界处是连续的并且准确地逼近数据。Akima 的方法同时考虑了数据点的斜率和曲率,从而产生更平滑和更具视觉吸引力的插值。
Akima优势
Akima 拟合的优势之一是它能够处理间隔不均匀的数据点,使其适用于不规则采样的数据。该算法还解决了数据点突然变化或不连续的情况。
算法的代码实现
鉴于很多是嵌入式上用Akima算法,这里在python版之外还提供了C++版。
python版
需要scipy包,里面直接有Akima拟合函数。
x,y是自己定义的需要Akima拟合的曲线的坐标,把这些坐标放到akima_interpolator里去。
然后将一个新的x输入akima_interpolator就能得到拟合的y了,是不是很简单。
import numpy as np
from scipy.interpolate import Akima1DInterpolator# Generate sample data
x = np.array([1, 2, 3, 4, 5])
y = np.array([1, 3, 2, 5, 4])# Perform Akima fitting
akima_interpolator = Akima1DInterpolator(x, y)# Generate new x-values for interpolation
x_new = np.linspace(1, 5, num=100)# Interpolate y-values using Akima fitting
y_new = akima_interpolator(x_new)# Print the interpolated values
for i in range(len(x_new)):print(f"x: {x_new[i]}, y: {y_new[i]}")C++ 版
前面的python版全程用akima包,细节看不到,C++没有这种包,但我们能清楚看到里面细节。
#include <iostream>
#include <vector>
#include <cmath>// Akima插值函数
double akimaInterpolation(double x, const std::vector<double>& xData, const std::vector<double>& yData) {int n = xData.size();int index = 0;// Find the interval indexfor (int i = 0; i < n - 1; ++i) {if (x >= xData[i] && x <= xData[i + 1]) {index = i;break;}}// 计算斜率std::vector<double> slopes(n - 1); //初始化n-1个默认值为0的元素for (int i = 0; i < n - 1; ++i) {double dx = xData[i + 1] - xData[i];double dy = yData[i + 1] - yData[i];slopes[i] = dy / dx; //计算每段之间的斜率}// 计算权重std::vector<double> weights(n - 1); //初始化n-1个默认值为0的元素for (int i = 2; i < n - 2; ++i) {weights[i] = std::abs(slopes[i + 1] - slopes[i - 1]); //计算这些权重的目的是确定每个间隔附近的斜坡的“强度”。这些权重随后用于插值公式中,以确保插值曲线的平滑性和连续性。}// 计算插值double dx = xData[index + 1] - xData[index];double t = (x - xData[index]) / dx; //参数 t 表示区间内的归一化位置,取值范围为 0 到 1//m0、m1、p0和p1是 Akima 插值公式中用于计算插值的系数double m0 = slopes[index] * dx; //详见代码解析1double m1 = slopes[index + 1] * dx;double p0 = (3 * weights[index] - 2 * m0 - m1) / dx; //这里的3,2系数是怎么来的详见代码解析2double p1 = (3 * weights[index + 1] - m0 - 2 * m1) / dx;//interpolatedValue 这个公式用于计算最终插值结果,详见代码解析3double interpolatedValue =yData[index] * (1 - t) * (1 - t) * (1 + 2 * t) +yData[index + 1] * t * t * (3 - 2 * t) +p0 * t * (1 - t) * (1 - t) +p1 * t * t * (t - 1);return interpolatedValue;
}int main() {std::vector<double> xData = {1, 2, 3, 4, 5};std::vector<double> yData = {1, 3, 2, 5, 4};// 假设输入一个x=2.5,y输出多少?double interpolatedValue = akimaInterpolation(2.5, xData, yData);std::cout << "Interpolated value at x = 2.5: " << interpolatedValue << std::endl;return 0;
}解释一下上面的斜率和权重,斜率是通过相邻点之间 k=dy/dx 来计算。而权重是区间附近斜率对这个区间影响的权重,将点i的左侧斜率slopes[i - 1]和右侧斜率slopes[i + 1]相减得到,存在weights[i]里。权重随后用于插值公式中,以确保插值曲线的平滑性和连续性。
这里展开讲一下:
在 Akima 插值中,插值曲线是通过将分段三次曲线拟合到连续数据点之间的每个区间来构建的。这些三次曲线的斜率在确定插值曲线的形状和行为方面起着至关重要的作用。目标是确保曲线连续并遵循数据的总体趋势,同时避免过度振荡。
通过计算权重算法考虑了相邻区间之间斜率的变化。权重通过捕获数据的局部行为并影响插值过程中每个斜率的“强度”。较大的权重表示区域斜率变化明显,而较小的权重表示区域较平滑。
在执行插值时,将权重合并到插值公式中以调整相邻斜率的贡献。权重充当控制不同区间斜率之间平衡的系数。此调整有助于平滑插值曲线并减少由异常值或噪声数据点引起的突然变化。
代码解析1
m0、m1、p0和p1是 Akima 插值公式中用于计算插值的系数:
m0:此变量表示左相邻区间的调整斜率。将当前区间 (slopes[index]) 的斜率乘以区间宽度 ( dx)得到。
m1:此变量表示右相邻区间的调整斜率。将下一个区间 (slopes[index + 1]) 的斜率乘以区间的宽度 (dx)得到。
p0:此变量表示左相邻区间的调整权重。它是使用当前区间 ( weights[index]) 的权重、左侧区间的调整斜率 ( m0) 和右侧区间的调整斜率 (m1) 计算得到。由公式(3 * weights[index] - 2 * m0 - m1) / dx确定左相邻区间对插值的贡献。
p1:此变量表示右相邻区间的调整权重。它是使用下一个区间的权重 ( weights[index + 1])、左侧区间的调整斜率 (m0) 和右侧区间的调整斜率 (m1) 计算得到。由公式(3 * weights[index + 1] - m0 - 2 * m1) / dx确定右相邻区间对插值的贡献。
代码解析2
公式(3 * weights[index] - 2 * m0 - m1) / dx 和 (3 * weights[index + 1] - m0 - 2 * m1) / dx 是基于Akima插值方案推导出来的。
为了理解推导,让我们考虑 Akima 插值方案的一般形式:
y(x) = p0(x) * y0 + p1(x) * y1 + q0(x) * m0 + q1(x) * m1
在此等式中,y(x)表示特定坐标处的插值x。y0和y1是x两侧的数据点, m0和m1是与数据点关联的斜率。项p0(x)和p1(x)是数据点的权重系数,q0(x)和q1(x)是数据点关联的斜率的权重系数。
为了确定p0(x)和p1(x),Akima 拟合使用三次多项式来确保平滑性和连续性。这些权重系数由斜率的局部行为决定。
通过考虑Akima插值方案,我们可以推导出代码中使用的具体权重公式:
对于p0(x):权重函数p0(x)决定了左邻域的贡献。在代码中,(3 * weights[index] - 2 * m0 - m1) / dx代表p0(x).
选择特定系数3、-2和1是为了平衡斜率的影响并确保间隔边界处的连续性。这些系数是通过数学分析和优化确定的。
对于p1(x):权重函数p1(x)决定了右邻区间的贡献。在代码中,(3 * weights[index + 1] - m0 - 2 * m1) / dx代表p1(x).同样,选择系数3、-1和-2以实现插值曲线的连续性和平滑性。
导出这些公式中的特定系数是为了最大限度地减少插值误差并保持曲线的连续性。它们是通过数学分析和优化技术确定的,以确保生成的曲线与基础数据点紧密匹配。
代码解析3
yData[index] * (1 - t) * (1 - t) * (1 + 2 * t):这一项代表左边数据点(yData [index]) 对插值的贡献。它乘以三次多项式“(1 - t) * (1 - t) * (1 + 2 * t)”,该多项式取决于参数“t”,范围从 0 到 1。多项式旨在确保左侧数据点的平滑过渡和适当加权。yData[index + 1] * t * t * (3 - 2 * t):此项表示右侧数据点 (yData[index + 1]) 对插值的贡献。它乘以三次多项式“t * t * (3 - 2 * t)”。与上面类似,这个多项式确保了右侧数据点的平滑过渡和适当加权。p0 * t * (1 - t) * (1 - t):此项表示左侧相邻区间的调整权重 (p0) 对插值的贡献。它乘以三次多项式“t * (1 - t) * (1 - t)”。该多项式表示左侧相邻区间对插值的影响。p1 * t * t * (t - 1):此项表示右相邻区间的调整权重 (p1) 对插值的贡献。它乘以三次多项式“t * t * (t - 1)”。该多项式表示右侧邻区间对插值的影响。
该方程结合了相邻数据点的贡献及其相应的权重来计算最终的插值。参数 t 表示区间内的归一化位置,取值范围为 0 到 1。它决定了相邻数据点及其对应区间的相对权重。应用于数据点和权重的三次多项式确保插值曲线的平滑性和连续性。
把上面这些影响因素加一起就是插值点的函数值interpolatedValue了。
C版
注:这是另一位博主写的,因为没有过多的备注信息,算法里参数配置也没有找到对应的文献支持。但是经实验也能起到插值的作用。
根据最后输出的 “s[4]=s[0]+s[1]p+s[2]pp+s[3]ppp” ,推测就是将输入的点拟合成一个三次多项式曲线,返回的s0 s1 s2 s3 分别是x0 x1 x2 x3的系数,最后生成了一个y=s0+s1x+s2x2+s3x3的拟合函数,最后通过代入x值求出插值y。
这个方法与前面提到的Akima 原版算法有不同之处,可能是这个作者自己改良过的Akima。
//
// Akima光滑插值
// n - 用多少个数据进行拟合
// t - 存放指定的插值点的值
// s[] - 一维数组,长度为5,其中s(0),s(1),s(2),s(3)返回三次多项式的系数,
// s(4)返回指定插值点t处的函数近似值f(t)(k<0时)或任意值(k>=0时)
// k - 控制参数,若k>=0,则只计算第k个子区间[x(k), x(k+1)]上的三次多项式的系数,一般取-1即可
//
float GetValueAkima(int n, float t, double* s, int k)
{int kk,m,l;float u[5];double p,q; // 初值memset(s, 0, 5*sizeof(float));// 特例处理if (n < 1){return s[4];}if (n == 1){s[4] = y[0]; //把y0初值给s[4]s[0] = s[4]; //x^0的系数初值为y0return s[4]; }if (n == 2){s[0] = y[0]; //x^0的系数初值为y0s[1]=(y[1]-y[0])/(x[1]-x[0]); //x^1的系数初值为(y[1]-y[0])/(x[1]-x[0]),这里用了斜截式s1就是斜率if (k<0) s[4]=(y[0]*(t-x[1])-y[1]*(t-x[0]))/(x[0]-x[1]); return s[4]; //两点式求解的变形(s[4]-y0)/(y1-y0)=(t-x0)/(x1-x0)} // 插值if (k<0){if(t <= x[1])kk = 0; //插值在所有拟合数据之前else if (t>=x[n-1]) kk=n-2; //插值在所有拟合数据之后else //插值在所有拟合数据之间{kk = 1;m = n;while (((kk-m)!=1)&&((kk-m)!=-1)){l=(kk+m)/2;if (t < x[l-1])m=l;else kk=l;}kk=kk-1;}}else kk=k;// 以下算法内容未找到对应的文献支持,如果有读者能找到请在评论区留言if (kk>=n-1)kk=n-2;u[2]=(y[kk+1]-y[kk])/(x[kk+1]-x[kk]); //相当于之前求斜率if (n==3){if (kk==0){u[3]=(y[2]-y[1])/(x[2]-x[1]); //求初始斜率u[4]=2.0f*u[3]-u[2]; //初始斜率和当前斜率相减u[1]=2.0f*u[2]-u[3]; //上面的反过来减u[0]=2.0f*u[1]-u[2]; //不知道啥意思}else{u[1]=(y[1]-y[0])/(x[1]-x[0]);u[0]=2.0f*u[1]-u[2];u[3]=2.0f*u[2]-u[1];u[4]=2.0f*u[3]-u[2];}} else{if (kk<=1){u[3]=(y[kk+2]-y[kk+1])/(x[kk+2]-x[kk+1]); if (kk==1){u[1]=(y[1]-y[0])/(x[1]-x[0]);u[0]=2.0f*u[1]-u[2];if (n==4)u[4]=2.0f*u[3]-u[2];else u[4]=(y[4]-y[3])/(x[4]-x[3]);}else{u[1]=2.0f*u[2]-u[3];u[0]=2.0f*u[1]-u[2];u[4]=(y[3]-y[2])/(x[3]-x[2]); }} else if (kk>=(n-3)){u[1]=(y[kk]-y[kk-1])/(x[kk]-x[kk-1]);if (kk==(n-3)){u[3]=(y[n-1]-y[n-2])/(x[n-1]-x[n-2]);u[4]=2.0f*u[3]-u[2];if (n==4) u[0]=2.0f*u[1]-u[2];else u[0]=(y[kk-1]-y[kk-2])/(x[kk-1]-x[kk-2]);} else{u[3]=2.0f*u[2]-u[1];u[4]=2.0f*u[3]-u[2];u[0]=(y[kk-1]-y[kk-2])/(x[kk-1]-x[kk-2]); }}else{ u[1]=(y[kk]-y[kk-1])/(x[kk]-x[kk-1]);u[0]=(y[kk-1]-y[kk-2])/(x[kk-1]-x[kk-2]);u[3]=(y[kk+2]-y[kk+1])/(x[kk+2]-x[kk+1]);u[4]=(y[kk+3]-y[kk+2])/(x[kk+3]-x[kk+2]); }}s[0] = fabs(u[3]-u[2]);s[1] = fabs(u[0]-u[1]);
// if ((fabs(s[0])<0.0000001)&&(fabs(s[1])<0.0000001))if ((s[0]+1.0f == 1.0f) && (s[1]+1.0f == 1.0f))p = (u[1]+u[2])/2.0f;elsep = (s[0]*u[1]+s[1]*u[2])/(s[0]+s[1]);s[0] = fabs(u[3]-u[4]);s[1] = fabs(u[2]-u[1]);
// if ((fabs(s[0])<0.0000001)&&(fabs(s[1])<0.0000001))if ((s[0]+1.0f==1.0f) && (s[1]+1.0f==1.0f))q = (u[2]+u[3])/2.0f;elseq = (s[0]*u[2]+s[1]*u[3])/(s[0]+s[1]);s[0] = y[kk];s[1] = p;s[3] = x[kk+1]-x[kk];s[2] = (3.0f*u[2]-2.0f*p-q)/s[3];s[3] = (q+p-2.0f*u[2])/(s[3]*s[3]);if (k<0){p=t-x[kk];s[4]=s[0]+s[1]*p+s[2]*p*p+s[3]*p*p*p;}return s[4];
}
实验对比
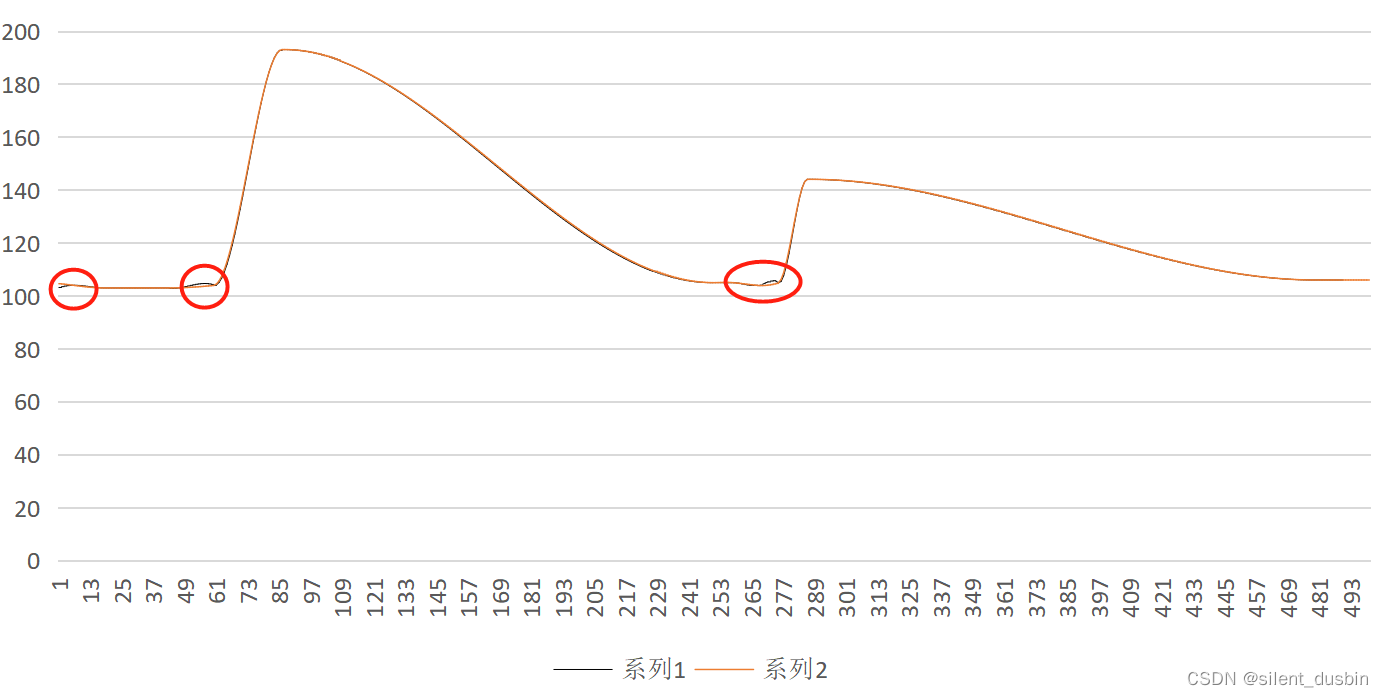
系列1是上面C++版的,系列2是C版的,可以看见经过C版Akima对于波动点的处理更好。笔者还在研究C版的原作者是怎么优化的,如果有知道的欢迎在评论区讨论。