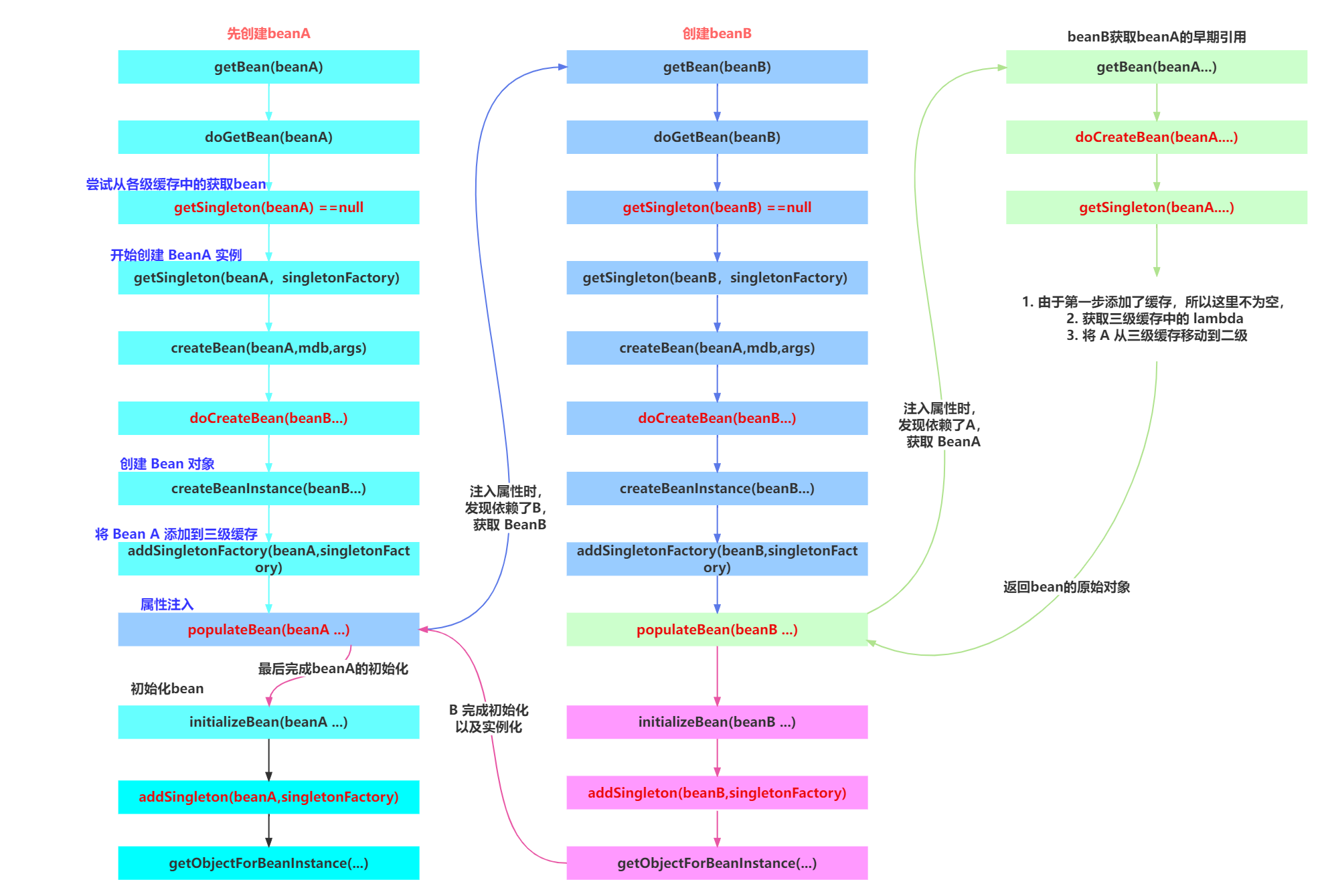
Cesium飞行定位方法中，destination和orientation参数之间的关系可以用以下数学公式表示：

1. 当只设置了destination参数时，相机保持当前朝向不变，直接飞往目标位置。

2. 当只设置了orientation参数时，相机以当前位置为起点，沿着指定的朝向方向飞行。

3. 当同时设置了destination和orientation参数时，相机需要在飞行过程中既要到达目标位置，又要按照指定的朝向进行旋转。这个问题可以通过计算相机的旋转矩阵来解决。具体地，假设相机当前位置为P0，目标位置为P1，相机当前的朝向为Q0，期望的朝向为Q1，则可以按照以下步骤计算相机的旋转矩阵：

• 计算相机当前位置与目标位置之间的方向向量D = normalize(P1 - P0)；
• 计算当前朝向Q0对应的旋转矩阵R0；
• 计算期望朝向Q1对应的旋转矩阵R1；
• 将R0和R1插值得到一个新的旋转矩阵Rt，其中插值系数由缓动函数控制；
• 将D和Rt组合得到最终的旋转矩阵Rf。

然后，可以将destination参数设置为目标位置P1，将orientation参数设置为旋转矩阵Rf，即可实现相机在飞行过程中保持朝向不变的效果。

在Cesium飞行定位中，destination和orientation参数之间的数学关系可以表示为：

假设当前相机位置为P0，目标位置为P1，当前朝向为Q0，期望朝向为Q1，pitch参数为α，则有：

1. 当只设置了destination参数时，相机保持当前朝向不变，直接飞往目标位置：

flyTo(P1, {orientation: Q0,pitch: α
});

1. 当只设置了orientation参数时，相机以当前位置为起点，沿着指定的朝向方向飞行：

let D = normalize(Q1 * Cartesian3.UNIT_Z); // 计算方向向量
let Rf = Matrix3.fromQuaternion(Quaternion.rotationBetween(Q0, D)); // 计算旋转矩阵
flyTo(P0, {orientation: Rf,pitch: α
});

1. 当同时设置了destination和orientation参数时，相机需要在飞行过程中既要到达目标位置，又要按照指定的朝向进行旋转。这个问题可以通过计算相机的旋转矩阵来解决：

let D = normalize(P1 - P0); // 计算方向向量
let R0 = Matrix3.fromQuaternion(Q0); // 计算当前朝向对应的旋转矩阵
let R1 = Matrix3.fromQuaternion(Q1); // 计算期望朝向对应的旋转矩阵
let Rt = Matrix3.lerp(R0, R1, t); // 计算插值后的旋转矩阵，t为插值系数
let Rf = Matrix3.multiply(Rt, Matrix3.fromRotationX(Cesium.Math.toRadians(α))); // 将pitch角度合并到旋转矩阵中
flyTo(P1, {orientation: Rf,pitch: 0
});

其中，normalize函数用于将向量归一化，Quaternion.rotationBetween函数用于计算两个四元数之间的旋转变换，Matrix3.lerp函数用于计算两个矩阵之间的线性插值。