【论文翻译】Deep learning

论文题目：Deep Learning
论文来源:Deep Learning_2015_Nature
翻译人：BDML@CQUT实验室

Deep learning allows computational models that are composed of multiple processing layers to learn representations of data with multiple levels of abstraction. These methods have dramatically improved the in speech recognition, visual object recognition, object detection and many other domains such as drug discovery and genomics. Deep learning discovers intricate structure in large data sets by using the backpropagation algorithm to indicate how a machine should change its internal parameters that are used to compute the representation in each layer from the representation in the previous layer. Deep convolutional nets have brought about breakthroughs in processing images, video, speech and audio, whereas recurrent nets have shone light on sequential data such as text and speech.

深度学习允许由多个处理层组成的计算模型去学习多层次抽象的数据表示。这些方法极大的提高了语音识别、视觉目标识别、目标检测和许多其他领域如药物发现和基因方面的最先进水平。深度学习通过使用反向传播算法来发现大型数据集中的复杂结构，指示机器应该如何改变其内部参数，这些参数用于从上一层的表现从而计算每一层的表现。深度卷积网络在处理图像、视频、语音和音频方面带来了突破性的进展，而递归网络则在文本和语音等处理顺序数据方面大放异彩。

Machine-learning technology powers many aspects of modern society: from web searches to content filtering on social networks to recommendations on e-commerce websites, and it is increasingly present in consumer products such as cameras and smartphones. Machine-learning systems are used to identify objects in images, transcribe speech into text, match news items, posts or products with users’ interests, and select relevant results of search. Increasingly, these applications make use of a class of techniques called deep learning.

Conventional machine-learning techniques were limited in their ability to process natural data in their raw form. For decades, constructing a pattern-recognition or machine-learning system required careful engineering and considerable domain expertise to design a feature extractor that transformed the raw data (such as the pixel values of an image) into a suitable internal representation or feature vector from which the learning subsystem, often a classifier, could detect or classify patterns in the input.

Representation learning is a set of methods that allows a machine to be fed with raw data and to automatically discover the representations needed for detection or classification. Deep-learning methods are representation-learning methods with multiple levels of representation, obtained by composing simple but non-linear modules that each transform the representation at one level (starting with the raw input) into a representation at a higher, slightly more abstract level. With the composition of enough such transformations, very complex functions can be learned.For classification tasks, higher layers of representation amplify aspects of the input that are important for discrimination and suppress irrelevant variations.An image, for example, comes in the form of an array of pixel values, and the learned features in the first layer of representation typically represent the presence or absence of edges at particular orientations and locations in the image.The second layer typically detects motifs by spotting particular arrangements of edges, regardless of small variations in the edge positions.The third layer may assemble motifs into larger combinations that correspond to parts of familiar objects, and subsequent layers would detect objects as combinations of these parts. The key aspect of deep learning is that these layers of features are not designed by human engineers: they are learned from data using a general-purpose learning procedure.

Deep learning is making major advances in solving problems that have resisted the best attempts of the artificial intelligence community for many years. It has turned out to be very good at discovering intricate structures in high-dimensional data and is therefore applicable to many domains of science, business and government. In addition to beating records in image recognition and speech recognition, it has beaten other machine-learning techniques at predicting the activity of potential drug molecules, analysing particle accelerator data, reconstructing brain circuits, and predicting the effects of mutations in non-coding DNA on gene expression and disease. Perhaps more surprisingly, deep learning has produced extremely promising results for various tasks in natural language understanding, particularly topic classification, sentiment analysis, question answering and language translation.

We think that deep learning will have many more successes in the near future because it requires very little engineering by hand, so it can easily take advantage of increases in the amount of available computation and data. New learning algorithms and architectures that are currently being developed for deep neural networks will only accelerate this progress.

机器学习技术为现代社会的许多方面提供了动力：从网络搜索到社交网络上的内容过滤，再到电子商务网站上的商品推荐，并且越来越多地出现在相机和智能手机等消费产品中。机器学习系统应用于图像中的目标识别、将语音转录为文本、将新闻、帖子或产品与用户的兴趣进行匹配，并选择相关的搜索结果。逐渐的，这些应用越来越多地利用深度学习的技术.

传统的机器学习技术在处理原始形式的自然数据方面能力有限。几十年来，构建模式识别或机器学习系统需要精心的工程设计和相当多的领域专业知识，来设计一个特征提取器，它能从学习子系统，通常是分类器，它可以从中检测或分类输入的模式，能够将原始数据，如图像的像素值转化为合适的内部表示或特征向量。

表征学习是一组方法，它可以让机器获得原始数据，并自动发现识别或分类所需的表征。深度学习方法是具有多种表现形式的表征学习方法，其通过组成简单但非线性的模块获得，这些模块分别将一个级别的表示，从原始输入开始，转换为更高的、稍微更抽象的级别的表示。通过组成足够多的这种变换，可以学习到非常复杂的函数。对于分类任务来说，更高的表示层加强了输入中对重要方面的识别，并抑制了不相关的变化。例如，一幅图像以像素值阵列的形式出现，第一层中学习到的特征点通常表示图像中特定方向和位置上是否存在边缘。第二层通常通过发现边缘的特定排列来识别图案，而不管边缘位置的微小变化。第三层可以将这些图案组成更大的组合体，这些组合对应于熟悉的物体的部分，并且随后的层将识别物体作为这些部分的组合。深度学习的关键方面是这些特征层并不是由人类工程师设计的，而是使用一般用途的学习程序从数据中学习得到的。

深度学习在解决多年来抵制人工智能界快速发展问题上取得了重大进展。事实证明，它非常善于发现高维度数据中复杂的结构，因此适用于科学、商业和政府的许多领域。除了在图像识别和语音识别方面取得了新记录外，它还在预测潜在药物分子的活性、分析粒子加速器数据、重建脑回路、以及预测非编码DNA突变对基因表达和疾病的影响等方面击败了其他机器学习技术。更令人惊讶的是，深度学习已经为自然语言中理解各种任务，特别是话题分类、情感分析、问题回答和语言翻译等方面带来了极大的成果。

我们认为，深度学习在不久的将来会有更多的成功，因为它只需要很少的人类操作工程，所以它可以很容易地利用可用计算量和数据量的增加，目前正在为深度神经网络开发的新的学习算法和架构会加速这种进步。

Supervised learning

The most common form of machine learning, deep or not, is supervised learning. Imagine that we want to build a system that can classify images as containing, say, a house, a car, a person or a pet. We first collect a large data set of images of houses, cars, people and pets, each labelled with its category. During training, the machine is shown an image and produces an output in the form of a vector of scores, one for each category.We want the desired category to have the highest score of all categories, but this is unlikely to happen before training. We compute an objective function that measures the error (or distance) between the output scores and the desired pattern of scores. The machine then modifies its internal adjustable parameters to reduce this error. These adjustable parameters, often called weights, are real numbers that can be seen as ‘knobs’ that define the input–output function of the machine. In a typical deep-learning system, there may be hundreds of millions of these adjustable weights, and hundreds of millions of labelled examples with which to train the machine.

To properly adjust the weight vector, the learning algorithm computes a gradient vector that, for each weight, indicates by what amount the error would increase or decrease if the weight were increased by a tiny amount. The weight vector is then adjusted in the opposite direction to the gradient vector.

The objective function, averaged over all the training examples, can be seen as a kind of hilly landscape in the high-dimensional space of weight values. The negative gradient vector indicates the direction of steepest descent in this landscape, taking it closer to a minimum, where the output error is low on average.

In practice, most practitioners use a procedure called stochastic gradient descent (SGD). This consists of showing the input vector for a few examples, computing the outputs and the errors, computing the average gradient for those examples, and adjusting the weights accordingly. The process is repeated for many small sets of examples from the training set until the average of the objective function stops decreasing. It is called stochastic because each small set of examples gives a noisy estimate of the average gradient over all examples. This simple procedure usually finds a good set of weights surprisingly quickly when compared with far more elaborate optimization techniques18. After training, the performance of the system is measured on a different set of examples called a test set. This serves to test the generalization ability of the machine — its ability to produce sensible answers on new inputs that it has never seen during training.

Many of the current practical applications of machine learning use linear classifiers on top of hand-engineered features. A two-class linear classifier computes a weighted sum of the feature vector components. If the weighted sum is above a threshold, the input is classified as belonging to a particular category.

Since the 1960s we have known that linear classifiers can only carve their input space into very simple regions, namely half-spaces separated by a hyperplane. But problems such as image and speech recognition require the input–output function to be insensitive to irrelevant variations of the input, such as variations in position, orientation or illumination of an object, or variations in the pitch or accent of speech, while being very sensitive to particular minute variations (for example, the difference between a white wolf and a breed of wolf-like white dog called a Samoyed). At the pixel level, images of two Samoyeds in different poses and in different environments may be very different from each other, whereas two images of a Samoyed and a wolf in the same position and on similar backgrounds may be very similar to each other. A linear classifier, or any other ‘shallow’ classifier operating on raw pixels could not possibly distinguish the latter two, while putting the former two in the same category. This is why shallow classifiers require a good feature extractor that solves the selectivity–invariance dilemma — one that produces representations that are selective to the aspects of the image that are important for discrimination, but that are invariant to irrelevant aspects such as the pose of the animal. To make classifiers more powerful, one can use generic non-linear features, as with kernel methods, but generic features such as those arising with the Gaussian kernel do not allow the learner to generalize well far from the training examples. The conventional option is to hand design good feature extractors, which requires a considerable amount of engineering skill and domain expertise. But this can all be avoided if good features can be learned automatically using a general-purpose learning procedure. This is the key advantage of deep learning.

A deep-learning architecture is a multilayer stack of simple modules, all (or most) of which are subject to learning, and many of which compute non-linear input–output mappings. Each module in the stack transforms its input to increase both the selectivity and the invariance of the representation. With multiple non-linear layers, say a depth of 5 to 20, a system can implement extremely intricate functions of its inputs that are simultaneously sensitive to minute details — distinguishing Samoyeds from white wolves — and insensitive to large irrelevant variations such as the background, pose, lighting and surrounding objects.

Figure 1 | Multilayer neural networks and backpropagation.
a, A multilayer neural network (shown by the connected dots) can distort the input space to make the classes of data (examples of which are on the red and blue lines) linearly separable. Note how a regular grid (shown on the left) in input space is also transformed (shown in the middle panel) by hidden units. This is an illustrative example with only two input units, two hidden units and one output unit, but the networks used for object recognition or natural language processing contain tens or hundreds of thousands of units. Reproduced with permission from C. Olah (http://colah.github.io/).
b, The chain rule of derivatives tells us how two small effects (that of a small change of x on y, and that of y on z) are composed. A small change Δx in x gets transformed first into a small change Δy in y by getting multiplied by ∂y/∂x (that is, the definition of partial derivative). Similarly, the change Δy creates a change Δz in z. Substituting one equation into the other gives the chain rule of derivatives — how Δx gets turned into Δz through multiplication by the product of ∂y/∂x and ∂z/∂x. It also works when x, y and z are vectors (and the derivatives are Jacobian matrices).
c, The equations used for computing the forward pass in a neural net with two hidden layers and one output layer, each constituting a module through which one can backpropagate gradients. At each layer, we first compute the total input z to each unit, which is a weighted sum of the outputs of the units in the layer below. Then a non-linear function f(.) is applied to z to get the output of the unit. For simplicity, we have omitted bias terms. The non-linear functions used in neural networks include the rectified linear unit (ReLU) f(z) = max(0,z), commonly used in recent years, as well as the more conventional sigmoids, such as the hyberbolic tangent, f(z) = (exp(z) − exp(−z))/(exp(z) + exp(−z)) and logistic function logistic, f(z) = 1/(1 + exp(−z)).
d, The equations used for computing the backward pass. At each hidden layer we compute the error derivative with respect to the output of each unit, which is a weighted sum of the error derivatives with respect to the total inputs to the units in the layer above. We then convert the error derivative with respect to the output into the error derivative with respect to the input by multiplying it by the gradient of f(z). At the output layer, the error derivative with respect to the output of a unit is computed by differentiating the cost function. This gives yl − tl if the cost function for unit l is 0.5(yl − tl)2, where tl is the target value. Once the ∂E/∂zk is known, the error-derivative for the weight wjk on the connection from unit j in the layer below is just yj ∂E/∂zk.

Figure 2 | Inside a convolutional network.
The outputs (not the filters) of each layer (horizontally) of a typical convolutional network architecture applied to the image of a Samoyed dog (bottom left; and RGB (red, green, blue) inputs, bottom right). Each rectangular image is a feature map corresponding to the output for one of the learned features, detected at each of the image positions. Information flows bottom up, with lower-level features acting as oriented edge detectors, and a score is computed for each image class in output. ReLU, rectified linear unit.

机器学习最常见的形式，不管是不是深度学习，都是监督学习。如果我们想建立一个系统，可以将图像分类，比如说，包含房子、汽车、人或宠物。我们首先收集一个大的数据集，这个数据集包括房子、汽车、人和宠物的图像，每个图像都标有它自己的类别。在训练过程中，机器会显示一张图像，并以向量表示分数的形式产生输出，每个类别都有一个分数。我们希望所需的类别在所有类别中得分最高，但这在训练前不太可能发生。我们计算一个目标函数，用来衡量输出分数与所期望模式之间的误差或距离。然后，机器会修改其内部的可调整的参数来减少这个误差。这些可调参数，通常被称为权重，是实数，可以看作是定义机器的输入输出函数的 “旋钮”。在一个典型的深度学习系统中，可能会有数以亿计的这些可调节权重和标签化例子来训练这些机器。

为了适当地调整权重向量，学习算法计算出一个梯度向量，对于每个权重，这个梯度向量就会得出如果权重增加一个微小的量，误差会增加或减少多少，然后将权重向量调整到与梯度向量相反的方向。

对所有训练实例平均分配到目标函数，可以看作是高维权值空间中的一种丘陵景观。负梯度向量表面这是这种种景观中最陡峭的下降方向，使其接近最小值，在这种情况下，输出误差平均较低。

在实践中，大多数从业者使用一种称为随机梯度下降，即SGD的程序，这包括显示几个例子的输入向量，计算输出和误差，计算这些例子的平均梯度，并相应调整权重。对训练集的许多小例子重复这个过程，直到目标函数的平均值停止下降。之所以称为随机，是因为每一个小例子集都给出了所有例子的平均梯度的噪声估计。这种简单的程序通常与更复杂的优化技术相比，很快就能找到一组好的权重，令人惊讶。训练结束后，系统的性能是在不同的测试集上测量的，这是为了测试机器的泛化能力，即它在训练期间从未见过的新输入数据上，能够生合理答案的能力。

目前很多机器学习的实际应用都是在手工设计的特征之上使用线性分类器。两类线性分类器计算特征向量分量的加权和。如果加权和高于一个阈值，输入就会被分类为属于某个类别。

自20世纪60年代以来，我们就知道线性分类器只能将输入空间划分为非常简单的区域，即由超平面分隔的半空间。但图像和语音识别等问题要求输入输出函数对输入的不相关变化不敏感，如物体的位置、方向或光照度的变化，或语音的音调或口音的变化，而对特定的微小变化，例如，白狼和被称为萨摩耶德的狼类白狗品种之间的差异非常敏感。在像素级别上，两只萨摩耶犬在不同姿势和不同环境下的图像可能彼此非常不同，而两只萨摩耶犬和狼在相同姿势和相似背景下的图像可能彼此非常相似。一个线性分类器，或者其他任何在原始像素上操作的浅层分类器都不可能将后两者区分开来，从而将前两者归为同一类。这就是为什么浅层分类器需要一个好的特征提取器来解决选择性不变性的难题，它产生的表征对图像中的识别很重要的方面是有选择性的，但对不相关的方面，如动物的姿势是不变的。为了使分类器更加强大，人们可以使用通用的非线性特征，就像内核方法一样，但是通用的特征，如高斯内核产生的特征，不允许学习者在远离训练实例的地方进行良好的泛化。传统的选择是手工设计好的特征提取器，这需要相当多的工程技能和领域专业知识。但如果能使用通用的学习程序自动学习好的特征，这一切都可以避免。这是深度学习的关键优势。

深度学习架构是一个由简单模块组成的多层堆栈架构，所有的或绝大部分模块都要进行学习，其中很多模块计算非线性的输入输出映射，堆栈中的每个模块都会对其输入进行变换，以增加表示的选择性和不变性。有了多个非线性层，比如5到20个深度，一个系统就可以对其输入实现极其复杂的功能，这些功能同时对微小的细节敏感如区分萨摩耶犬和白狼，而对大的不相关的变化如背景、姿势、灯光和周围的物体不敏感。

图1 多层神经网络和反向传播
a:多层神经网络，由连接的小点显示，可以扭曲输入空间，使数据的类别如例子在红线和蓝线上，可以线性分离。请注意，输入空间中的规则网格如左图所示，如何将被隐藏单元转化如中图所示。这是一个只有两个输入单元、两个隐藏单元和一个输出单元的说明性例子，但用于对象识别或自然语言处理的网络包含数万或数十万个单元。经C.Olah(http://colah.github.io/)授权转载。
b、导数链规则告诉我们两个小的效应，x对y的小变化，和y对z的小变化是如何构成的。x的一个微小变化Δx通过得到乘以∂y/∂x，首先转化为y的一个小变化Δy，即部分导数的定义。将一个方程代入另一个方程，就得到了导数的连锁规则Δx如何通过乘以∂y/∂x和∂z/∂x的乘积而变成Δz。当x、y和z是向量时，它也能起作用。
c、这个方程用于计算神经网中的前传，神经网有两层隐藏层和一层输出层，每一层构成一个模块，通过这个模块可以反推梯度。在每一层，我们首先计算每个单元的总输入z，它是下面一层单元输出的加权和。然后将一个非线性函数f(.)应用于z，得到单元的输出。为了简单起见，我们省略了偏置项。神经网络中使用的非线性函数包括近年来常用的整流线性单元(ReLU)f(z)=max(0,z)，以及比较传统的sigmoids，如hyberbolic切线，f(z)=(exp(z)-exp(-z))/(exp(z)+exp(-z))和logistic函数logistic，f(z)=1/(1+exp(-z))。
d、用于计算后的公式，在每个隐藏层，我们计算相对于每个单元的输出的误差导数，它是相对于上一层单元的总输入的误差导数的加权和。然后，我们将相对于输出的误差导数乘以f(z)的梯度，转换成相对于输入的误差导数。在输出层，相对于单位输出的误差导数是通过微分成本函数计算出来的。如果单位l的成本函数为0.5(yl-
tl)2，其中tl为目标值，则给出yl - tl。一旦知道了∂E/∂zk，那么从下层单位j的连接上的权重wjk的误差推导就只是yj ∂E/∂zk。

图2 卷积网络内部
一个典型的卷积网络架构应用于萨摩耶犬图像，左下角和右下角为RGB红、绿、蓝输入的每一层在水平方向的输出不是滤波器。每个矩形图像是一个特征图对应于输出的一个学习特征，在每个图像位置检测到。信息自下而上流动，低级特征作为定向边缘检测器，在输出中为每个图像类计算得分。ReLU，整流线性单元。

Backpropagation to train multilayer architectures

From the earliest days of pattern recognition, the aim of researchers has been to replace hand-engineered features with trainable multilayer networks, but despite its simplicity, the solution was not widely understood until the mid 1980s. As it turns out, multilayer architectures can be trained by simple stochastic gradient descent. As long as the modules are relatively smooth functions of their inputs and of their internal weights, one can compute gradients using the backpropagation procedure. The idea that this could be done, and that it worked, was discovered independently by several different groups during the 1970s and 1980s.

The backpropagation procedure to compute the gradient of an objective function with respect to the weights of a multilayer stack of modules is nothing more than a practical application of the chain rule for derivatives. The key insight is that the derivative (or gradient) of the objective with respect to the input of a module can be computed by working backwards from the gradient with respect to the output of that module (or the input of the subsequent module) (Fig. 1). The backpropagation equation can be applied repeatedly to propagate gradients through all modules, starting from the output at the top (where the network produces its prediction) all the way to the bottom (where the external input is fed). Once these gradients have been computed, it is straightforward to compute the gradients with respect to the weights of each module.

Many applications of deep learning use feedforward neural network architectures (Fig. 1), which learn to map a fixed-size input (for example, an image) to a fixed-size output (for example, a probability for each of several categories). To go from one layer to the next, a set of units compute a weighted sum of their inputs from the previous layer and pass the result through a non-linear function. At present, the most popular non-linear function is the rectified linear unit (ReLU), which is simply the half-wave rectifier f(z) = max(z, 0). In past decades, neural nets used smoother non-linearities, such as tanh(z) or 1/(1 + exp(−z)), but the ReLU typically learns much faster in networks with many layers, allowing training of a deep supervised network without unsupervised pre-training. Units that are not in the input or output layer are conventionally called hidden units. The hidden layers can be seen as distorting the input in a non-linear way so that categories become linearly separable by the last layer (Fig. 1).

In the late 1990s, neural nets and backpropagation were largely forsaken by the machine-learning community and ignored by the computer-vision and speech-recognition communities. It was widely thought that learning useful, multistage, feature extractors with little prior knowledge was infeasible. In particular, it was commonly thought that simple gradient descent would get trapped in poor local minima — weight configurations for which no small change would reduce the average error.

In practice, poor local minima are rarely a problem with large networks. Regardless of the initial conditions, the system nearly always reaches solutions of very similar quality. Recent theoretical and empirical results strongly suggest that local minima are not a serious issue in general. Instead, the landscape is packed with a combinatorially large number of saddle points where the gradient is zero, and the surface curves up in most dimensions and curves down in the remainder. The analysis seems to show that saddle points with only a few downward curving directions are present in very large numbers, but almost all of them have very similar values of the objective function. Hence, it does not much matter which of these saddle points the algorithm gets stuck at.

Interest in deep feedforward networks was revived around 2006 (refs 31–34) by a group of researchers brought together by the Canadian Institute for Advanced Research (CIFAR). The researchers introduced unsupervised learning procedures that could create layers of feature detectors without requiring labelled data. The objective in learning each layer of feature detectors was to be able to reconstruct or model the activities of feature detectors (or raw inputs) in the layer below. By ‘pre-training’ several layers of progressively more complex feature detectors using this reconstruction objective, the weights of a deep network could be initialized to sensible values. A final layer of output units could then be added to the top of the network and the whole deep system could be fine-tuned using standard backpropagation. This worked remarkably well for recognizing handwritten digits or for detecting pedestrians, especially when the amount of labelled data was very limited.

The first major application of this pre-training approach was in speech recognition, and it was made possible by the advent of fast graphics processing units (GPUs) that were convenient to program and allowed researchers to train networks 10 or 20 times faster. In 2009, the approach was used to map short temporal windows of coefficients extracted from a sound wave to a set of probabilities for the various fragments of speech that might be represented by the frame in the centre of the window. It achieved record-breaking results on a standard speech recognition benchmark that used a small vocabulary and was quickly developed to give record-breaking results on a large vocabulary task. By 2012, versions of the deep net from 2009 were being developed by many of the major speech groups6 and were already being deployed in Android phones. For smaller data sets, unsupervised pre-training helps to prevent overfitting, leading to significantly better generalization when the number of labelled examples is small, or in a transfer setting where we have lots of examples for some ‘source’ tasks but very few for some ‘target’ tasks. Once deep learning had been rehabilitated, it turned out that the pre-training stage was only needed for small data sets.

There was, however, one particular type of deep, feedforward network that was much easier to train and generalized much better than networks with full connectivity between adjacent layers. This was the convolutional neural network (ConvNet). It achieved many practical successes during the period when neural networks were out of favour and it has recently been widely adopted by the computervision community.

反向传播训练多层架构

从最早的模式识别开始，研究人员的目的就是用可训练的多层网络来代替手工设计的特征，但尽管它很简单，直到20世纪80年代中期，这个解决方案才被广泛理解。事实证明，多层架构可以通过简单的随机梯度下降来训练。只要模块的输入及其内部权重是相对平稳的函数，就可以使用反向传播程序计算其梯度。这个想法是可以做到的，而且是有效的，这是由几个不同的小组在20世纪70年代和80年代独立发现的。

计算目标函数相对于多层模块堆栈权重的梯度的反向传播过程，不过是导数链式规则的实际应用。最主要的是，目标函数相对于某个模块输入的导数或梯度可以通过对该模块输出或后续模块输入的梯度进行倒推计算，如图1。反向传播方程可以反复应用在所有模块中传播梯度，从顶部的输出即网络产生预测的地方，开始一直到底部即外部输入的地方。一旦计算出这些梯度，就可以直接计算出每个模块的权重的梯度。

深度学习的许多应用都使用前馈神经网络架构，如图1，它学习将一个固定大小的输入，例如，一个图像，映射到一个固定大小的输出，例如，几个类别中每个类别的概率。为了从一层到下一层，一组单元计算它们从上一层输入的加权和，并将结果通过一个非线性函数。目前，最流行的非线性函数是整流线性单元即ReLU，简单来说就是半波整流f(z)=max(z，0)。在过去的几十年里，神经网络使用了更平滑的非线性，如tanh(z)或1/(1+exp(-z))，但ReLU通常在具有许多层的网络中学习得更快，允许在没有无监督预训练的情况下训练深度监督网络。不在输入层或输出层的单元习惯上被称为隐藏单元。隐藏层可以看作是以非线性的方式对输入进行扭曲，使类别在最后一层变得可线性分离。

在20世纪90年代末，神经网和反向传播在很大程度上被机器学习界所抛弃，被计算机视觉和语音识别界所忽视。人们普遍认为，在几乎没有先验知识的情况下学习有用的、多阶段的特征提取器是不可行的。特别是，人们普遍认为，简单的梯度下降法会陷入局部最小值的困境，即权重配置的任何微小变化都不会减少平均误差。

在实践中，对于大型网络来说，表现差的局部最小值很少是一个问题。无论初始条件如何，系统几乎总是达到质量非常相似的解。最近的理论和经验结果强烈表明，局部最小值在一般情况下不是一个严重的问题。相反，景观被包装与梯度为零的大量鞍点的组合，和表面曲线在大多数维度和曲线除外。分析似乎表明，只有少数几个向下弯曲方向的鞍点以非常大的数量存在，但几乎所有鞍点的目标函数值都非常相似。因此，算法卡在这些鞍点中的哪一个并不太重要。

2006年前后，由加拿大高级研究所（CIFAR）召集的一组研究人员重新对深度前馈网络产生了兴趣。研究人员引入了无监督学习程序，可以在不需要标记数据的情况下创建特征检测器层。学习每一层特征检测器的目标是能够重建或模拟下一层特征检测器或原始输入的活动。通过使用这个重建目标来预训练几层逐渐复杂的特征检测器，深度网络的权重可以被初始化为合理的值。最后一层输出单元可以被添加到网络的顶部，整个深度系统可以使用标准的反向传播进行微调。这在识别手写数字或检测行人方面效果非常好，特别是当标签数据量非常有限时。

这种预训练方法的第一个主要应用是在语音识别中，它是由快速图形处理单元的出现而实现的，它方便编程，并允许研究人员以10或20倍的速度训练网络。2009年，该方法被用于将从声波中提取的系数的短时空窗口，映射为一组可能由窗口中心的帧所代表的各种语音片段的概率。它在使用小词汇量的标准语音识别基准上取得了破纪录的结果，并迅速发展到在大词汇量任务上给出破纪录的结果。到2012年，许多主要的语音集团都在开发2009年的深网版本，并且已经部署在Android手机中。对于较小的数据集，无监督的预训练有助于防止过度拟合，当标记的例子数量较少时，或者在转移环境中，我们对一些"源 "任务有很多例子，但对一些 "目标 "任务的例子很少时，会导致显著更好的泛化。一旦深度学习得到重建，就会发现预训练阶段只需要小数据集。

然而，有一种特殊类型的深层、前馈网络，比相邻层之间完全连接的网络更容易训练，泛化效果更好。这就是卷积神经网络。在神经网络不受欢迎的时期，它就取得了许多实际的成功，最近它被计算视觉界广泛采用。

Convolutional neural networks

ConvNets are designed to process data that come in the form of multiple arrays, for example a colour image composed of three 2D arrays containing pixel intensities in the three colour channels. Many data modalities are in the form of multiple arrays: 1D for signals and sequences, including language; 2D for images or audio spectrograms; and 3D for video or volumetric images. There are four key ideas behind ConvNets that take advantage of the properties of natural signals: local connections, shared weights, pooling and the use of many layers.

The architecture of a typical ConvNet (Fig. 2) is structured as a series of stages. The first few stages are composed of two types of layers: convolutional layers and pooling layers. Units in a convolutional layer are organized in feature maps, within which each unit is connected to local patches in the feature maps of the previous layer through a set of weights called a filter bank. The result of this local weighted sum is then passed through a non-linearity such as a ReLU. All units in a feature map share the same filter bank. Different feature maps in a layer use different filter banks. The reason for this architecture is twofold. First, in array data such as images, local groups of values are often highly correlated, forming distinctive local motifs that are easily detected. Second, the local statistics of images and other signals are invariant to location. In other words, if a motif can appear in one part of the image, it could appear anywhere, hence the idea of units at different locations sharing the same weights and detecting the same pattern in different parts of the array. Mathematically, the filtering operation performed by a feature map is a discrete convolution, hence the name.

Although the role of the convolutional layer is to detect local conjunctions of features from the previous layer, the role of the pooling layer is to merge semantically similar features into one. Because the relative positions of the features forming a motif can vary somewhat, reliably detecting the motif can be done by coarse-graining the position of each feature. A typical pooling unit computes the maximum of a local patch of units in one feature map (or in a few feature maps). Neighbouring pooling units take input from patches that are shifted by more than one row or column, thereby reducing the dimension of the representation and creating an invariance to small shifts and distortions. Two or three stages of convolution, non-linearity and pooling are stacked, followed by more convolutional and fully-connected layers. Backpropagating gradients through a ConvNet is as simple as through a regular deep network, allowing all the weights in all the filter banks to be trained.

Deep neural networks exploit the property that many natural signals are compositional hierarchies, in which higher-level features are obtained by composing lower-level ones. In images, local combinations of edges form motifs, motifs assemble into parts, and parts form objects. Similar hierarchies exist in speech and text from sounds to phones, phonemes, syllables, words and sentences. The pooling allows representations to vary very little when elements in the previous layer vary in position and appearance.

The convolutional and pooling layers in ConvNets are directly inspired by the classic notions of simple cells and complex cells in visual neuroscience, and the overall architecture is reminiscent of the LGN–V1–V2–V4–IT hierarchy in the visual cortex ventral pathway. When ConvNet models and monkeys are shown the same picture, the activations of high-level units in the ConvNet explains half of the variance of random sets of 160 neurons in the monkey’s inferotemporal cortex45. ConvNets have their roots in the neocognitron, the architecture of which was somewhat similar, but did not have an end-to-end supervised-learning algorithm such as backpropagation. A primitive 1D ConvNet called a time-delay neural net was used for the recognition of phonemes and simple words.

There have been numerous applications of convolutional networks going back to the early 1990s, starting with time-delay neural networks for speech recognition and document reading. The document reading system used a ConvNet trained jointly with a probabilistic model that implemented language constraints. By the late 1990s this system was reading over 10% of all the cheques in the United States. A number of ConvNet-based optical character recognition and handwriting recognition systems were later deployed by Microsoft. ConvNets were also experimented with in the early 1990s for object detection in natural images, including faces and hands, and for face recognition.

卷积神经网络

ConvNets被设计用来处理以多个数组形式出现的数据，例如，一幅彩色图像由三个二维数组组成，其中包含三个颜色通道中的像素强度。许多数据方式都是以多个数组的形式出现的。1D的信号和序列，包括语言；2D的图像或音频谱图；3D的视频或体积图像。ConvNets背后有四个关键思想，即利用了自然信号的特性：局部连接、共享权重、池化和使用许多层。

一个典型的ConvNet的架构如图2，是由一系列阶段组成的。前几个阶段由两种类型的层组成：卷积层和池化层。卷积层中的单元被组织在特征图中，在特征图中，每个单元通过一组称为滤波库的权重与上一层特征图中的局部补丁相连。这个局部加权和的结果再通过一个非线性组件，如ReLU，一个特征图中的所有单元共享同一个滤波库。一个层中的不同特征图使用不同的滤波库。这种架构的原因有两个方面。首先，在图像等阵列数据中，局部的数值组往往高度相关，形成独特的局部图案，容易被检测到。其次，图像和其他信号的局部统计量相对位置是不变的。换句话说，如果一个图案可以出现在图像的某一部分，那么它可能出现在任何地方，因此，不同位置的单元共享相同的权重，在阵列的不同部分检测相同的图案。从数学上讲，特征图进行的滤波操作是一种离散卷积。

虽然卷积层的作用是检测上一层特征的局部联合，但池化层的作用是将语义相似的特征合并成一个特征。由于构成图案的特征的相对位置可能会有一定的变化，因此可以通过对每个特征的位置进行粗粒度检测，从而来可靠地检测图案。一个典型的池化单元计算一个特征图中或几个特征图中的局部斑块单元的最大值。邻近的池化单元从偏移超过一行或一列的斑块中获取输入，从而降低了表示的维度，并对小的偏移和失真产生了不变性。卷积、非线性和池化的两个或三个阶段被堆叠起来，然后是更多的卷积层和全连接层。通过ConvNet反传播梯度就像通过普通的深度网络一样简单，可以训练所有滤波器库中的所有权重。

深度神经网络利用了许多自然信号是组成层次结构的特性，其中高层次的特征是通过组成低层次的特征来获得的。在图像中，边缘的局部组合形成图案，图案组合成部件，部件形成对象。在语音和文本中，从声音到电话、音素、音节、单词和句子都存在类似的层次结构。当前一层的元素在位置和外观上发生变化时，池化使得表征的变化很小。

ConvNets中的卷积层和汇集层直接受到视觉神经科学中简单细胞和复杂细胞的经典概念的启发，整体架构让人联想到视觉皮层腹侧通路中的LGN-V1-V2-V4-IT层次结构。当ConvNet模型和猴子显示相同的图片，ConvNet中高级单位的激活解释了猴子的下颞皮层160个神经元随机集的一半方差。ConvNets的根源在于新认知器，其架构有些类似，但没有端到端监督学习算法，如反向传播。一种被称为延时神经网的原始1D ConvNet被用于音素和简单单词的识别。

卷积网络的大量应用可以追溯到20世纪90年代初，首先是用于语音识别和文档阅读的时间延迟神经网络。文档阅读系统使用一个ConvNet与一个实现语言约束的概率模型联合训练。到20世纪90年代末，这个系统已经读取了美国所有支票的10%以上。后来微软公司部署了一些基于ConvNet的光学字符识别和手写识别系统。在90年代初，ConvNets还被实验用于自然图像中的物体检测，包括人脸和手以及人脸识别。

Image understanding with deep convolutional networks

Since the early 2000s, ConvNets have been applied with great success to the detection, segmentation and recognition of objects and regions in images. These were all tasks in which labelled data was relatively abundant, such as traffic sign recognition, the segmentation of biological images particularly for connectomics, and the detection of faces, text, pedestrians and human bodies in natural images .A major recent practical success of ConvNets is face recognition .

Importantly, images can be labelled at the pixel level, which will have applications in technology, including autonomous mobile robots and self-driving cars. Companies such as Mobileye and NVIDIA are using such ConvNet-based methods in their upcoming vision systems for cars. Other applications gaining importance involve natural language understanding and speech recognition.

Figure 3 | From image to text.
Captions generated by a recurrent neural network (RNN) taking, as extra input, the representation extracted by a deep convolution neural network (CNN) from a test image, with the RNN trained to ‘translate’ high-level representations of images into captions (top). Reproduced with permission from ref. 102. When the RNN is given the ability to focus its attention on a different location in the input image (middle and bottom; the lighter patches were given more attention) as it generates each word (bold), we found that it exploits this to achieve better ‘translation’ of images into captions.

Despite these successes, ConvNets were largely forsaken by the mainstream computer-vision and machine-learning communities until the ImageNet competition in 2012. When deep convolutional networks were applied to a data set of about a million images from the web that contained 1,000 different classes, they achieved spectacular results, almost halving the error rates of the best competing approaches1. This success came from the efficient use of GPUs, ReLUs, a new regularization technique called dropout, and techniques to generate more training examples by deforming the existing ones. This success has brought about a revolution in computer vision; ConvNets are now the dominant approach for almost all recognition and detection tasks and approach human performance on some tasks. A recent stunning demonstration combines ConvNets and recurrent net modules for the generation of image captions (Fig. 3).

Recent ConvNet architectures have 10 to 20 layers of ReLUs, hundreds of millions of weights, and billions of connections between units. Whereas training such large networks could have taken weeks only two years ago, progress in hardware, software and algorithm parallelization have reduced training times to a few hours.

The performance of ConvNet-based vision systems has caused most major technology companies, including Google, Facebook, Microsoft, IBM, Yahoo!, Twitter and Adobe, as well as a quickly growing number of start-ups to initiate research and development projects and to deploy ConvNet-based image understanding products and services.

ConvNets are easily amenable to efficient hardware implementations in chips or field-programmable gate arrays. A number of companies such as NVIDIA, Mobileye, Intel, Qualcomm and Samsung are developing ConvNet chips to enable real-time vision applications in smartphones, cameras, robots and self-driving cars.

用深度卷积网络理解图像

自2000年初以来，ConvNets被成功地应用于图像中物体和区域的检测、分割和识别。这些都是标签数据相对丰富的任务，如交通标志识别，生物图像的分割特别是连接组学，以及自然图像中人脸、文本、行人和人体的检测.ConvNets最近取得的一个主要的实际成功是人脸识别。

更重要的是，图像可以在像素级进行标记，这将在技术上得到应用，包括自主移动机器人和自动驾驶汽车。Mobileye和英伟达等公司正在他们即将推出的汽车视觉系统中使用这种基于ConvNet的方法。其他越来越重要的应用涉及自然语言理解和语音识别领域。

图3 从图像到文本
由循环神经网络(RNN)生成的文本，将深度卷积神经网络(CNN)从测试图像中提取的表征作为额外的输入，RNN被训练成将图像的高级表征 "翻译 "成文本。当RNN在生成每个单词（粗体）时，能够将注意力集中在输入图像中的不同位置，较轻的补丁被给予更多的关注，我们发现它利用这一点来实现更好地将图像 "翻译 "成文本。

尽管取得了这些成功，但ConvNets在很大程度上被主流计算机视觉和机器学习社区所抛弃，直到2012年的ImageNet竞赛。当深度卷积网络被应用于包含1000个不同类别的约100万张网络图像的数据集时，它们取得了惊人的结果，几乎将最佳竞争方法的错误率降低了一半。这种成功来自于GPU、ReLU、一种称为dropout的新正则化技术以及通过变形现有例子来生成更多训练例子的技术的有效使用。这一成功带来了计算机视觉的革命；ConvNets现在是几乎所有识别和检测任务的主导方法，并在一些任务上接近人类的性能。最近的一个惊人的演示结合了ConvNets和循环网模块来生成图像标题。

最近的ConvNet架构有10到20层的ReLU，数亿个权重，单元之间有数十亿个连接。仅在两年前，训练这样的大型网络可能需要数周的时间，而硬件、软件和算法并行化的进展已经将训练时间缩短到了几个小时。

基于ConvNet的视觉系统的表现，使得包括谷歌、Facebook、微软、IBM、雅虎、Twitter和Adobe在内的大多数主要技术公司，以及迅速增长的初创企业纷纷启动研发项目，并部署基于ConvNet的图像理解产品和服务。

ConvNets很容易在芯片或现场可编程门阵列中进行高效的硬件实现。英伟达、Mobileye、英特尔、高通和三星等多家公司正在开发ConvNet芯片，以实现智能手机、相机、机器人和自动驾驶汽车的实时视觉应用。

Distributed representations and language processing

Deep-learning theory shows that deep nets have two different exponential advantages over classic learning algorithms that do not use distributed representations. Both of these advantages arise from the power of composition and depend on the underlying data-generating distribution having an appropriate componential structure. First, learning distributed representations enable generalization to new combinations of the values of learned features beyond those seen during training (for example, 2n combinations are possible with n binary features). Second, composing layers of representation in a deep net brings the potential for another exponential advantage(exponential in the depth).

The hidden layers of a multilayer neural network learn to represent the network’s inputs in a way that makes it easy to predict the target outputs. This is nicely demonstrated by training a multilayer neural network to predict the next word in a sequence from a local context of earlier words. Each word in the context is presented to the network as a one-of-N vector, that is, one component has a value of 1 and the rest are 0. In the first layer, each word creates a different pattern of activations, or word vectors (Fig. 4). In a language model, the other layers of the network learn to convert the input word vectors into an output word vector for the predicted next word, which can be used to predict the probability for any word in the vocabulary to appear as the next word. The network learns word vectors that contain many active components each of which can be interpreted as a separate feature of the word, as was first demonstrated in the context of learning distributed representations for symbols. These semantic features were not explicitly present in the input. They were discovered by the learning procedure as a good way of factorizing the structured relationships between the input and output symbols into multiple ‘micro-rules’. Learning word vectors turned out to also work very well when the word sequences come from a large corpus of real text and the individual micro-rules are unreliable .When trained to predict the next word in a news story, for example, the learned word vectors for Tuesday and Wednesday are very similar, as are the word vectors for Sweden and Norway. Such representations are called distributed representations because their elements (the features) are not mutually exclusive and their many configurations correspond to the variations seen in the observed data. These word vectors are composed of learned features that were not determined ahead of time by experts, but automatically discovered by the neural network. Vector representations of words learned from text are now very widely used in natural language applications.

The issue of representation lies at the heart of the debate between the logic-inspired and the neural-network-inspired paradigms for cognition. In the logic-inspired paradigm, an instance of a symbol is something for which the only property is that it is either identical or non-identical to other symbol instances. It has no internal structure that is relevant to its use; and to reason with symbols, they must be bound to the variables in judiciously chosen rules of inference. By contrast, neural networks just use big activity vectors, big weight matrices and scalar non-linearities to perform the type of fast ‘intuitive’ inference that underpins effortless commonsense reasoning.

Before the introduction of neural language models, the standard approach to statistical modelling of language did not exploit distributed representations: it was based on counting frequencies of occurrences of short symbol sequences of length up to N (called N-grams). The number of possible N-grams is on the order of VN, where V is the vocabulary size, so taking into account a context of more than a handful of words would require very large training corpora. N-grams treat each word as an atomic unit, so they cannot generalize across semantically related sequences of words, whereas neural language models can because they associate each word with a vector of real valued features, and semantically related words end up close to each other in that vector space (Fig. 4).

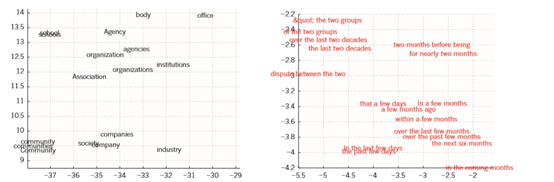
Figure 4 | Visualizing the learned word vectors.
On the left is an illustration of word representations learned for modelling language, non-linearly projected to 2D for visualization using the t-SNE algorithm. On the right is a 2D representation of phrases learned by an English-to-French encoder–decoder recurrent neural network. One can observe that semantically similar words or sequences of words are mapped to nearby representations. The distributed representations of words are obtained by using backpropagation to jointly learn a representation for each word and a function that predicts a target quantity such as the next word in a sequence (for language modelling) or a whole sequence of translated words (for machine translation).

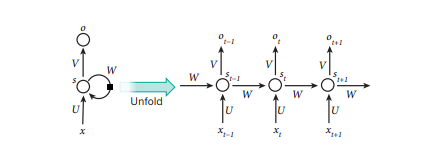
Figure 5 | A recurrent neural network and the unfolding in time of the computation involved in its forward computation.
The artificial neurons (for example, hidden units grouped under node s with values st at time t) get inputs from other neurons at previous time steps (this is represented with the black square, representing a delay of one time step, on the left). In this way, a recurrent neural network can map an input sequence with elements xt into an output sequence with elements ot, with each ot depending on all the previous xtʹ (for tʹ ≤ t). The same parameters (matrices U,V,W ) are used at each time step. Many other architectures are possible, including a variant in which the network can generate a sequence of outputs (for example, words), each of which is used as inputs for the next time step. The backpropagation algorithm (Fig. 1) can be directly applied to the computational graph of the unfolded network on the right, to compute the derivative of a total error (for example, the log-probability of generating the right sequence of outputs) with respect to all the states st and all the parameters.

分布式表示和语言处理

深度学习理论表明，与不使用分布式表示的经典学习算法相比，深度网络有两个不同的指数优势。这两个优势都来自于组成的力量，并取决于底层数据生成分布具有适当的成分结构。首先，学习分布式表征能够泛化到学习特征值的新组合，超出训练期间看到的组合，例如，2n种组合是可能的n个二进制特征。其次，在深度网络中组成层的表征带来了另一个指数优势的潜力，即深度的指数。

多层神经网络的隐藏层学习以一种易于预测目标输出的方式来表示网络的输入。这一点可以通过训练多层神经网络，从早期单词的局部上下文中预测序列中的下一个单词来很好地证明。语境中的每个单词都以one-of-N向量的形式呈现给网络，也就是说，一个分量的值是1，其余的都是0.在第一层，每个单词都会产生不同的激活模式，或者说单词向量。在语言模型中，网络的其他层学习将输入的单词向量转换为预测下一个单词的输出单词向量，它可以用来预测词汇中任何单词作为下一个单词出现的概率。该网络学习的单词向量包含许多活跃的组件，其中每个组件都可以被解释为单词的一个独立特征，就像在学习符号的分布式表征的背景下首次展示的那样。这些语义特征并没有明确地存在于输入中。它们被学习程序发现，作为将输入和输出符号之间的结构关系因子化为多个 "微规则 "的好方法。当单词序列来自于大量真实文本的语料库，且单个微规则不可靠时，学习单词向量的效果也非常好。例如，当训练预测一个新闻报道中的下一个单词时，周二和周三的学习单词向量非常相似，瑞典和挪威的单词向量也是如此。这种表征被称为分布式表征，因为它们的元素特征并不相互排斥，它们的许多配置对应于观察到的数据中的变化。这些词向量由学习到的特征组成，这些特征不是由专家提前确定的，而是由神经网络自动发现的。从文本中学习到的词的向量表示目前在自然语言应用中得到了非常广泛的应用。

表征问题是认知的逻辑启发范式和神经网络启发范式之间争论的核心，在逻辑启发范式中，一个符号的实例是一个东西，对它来说，唯一的属性是它与其他符号实例要么相同，要么不相同。它没有与其使用相关的内部结构；而要对符号进行推理，就必须将其与明智地选择的推理规则中的变量进行绑定。相比之下，神经网络只是使用大的活动向量、大的权重矩阵和标量非线性来执行那种快速的 "直觉 "推理，而这种推理是毫不费力的常识推理的基础。

在引入神经语言模型之前，语言统计建模的标准方法并没有利用分布式表征：它是基于计算长度不超过N的短符号序列，称为N-grams的出现频率。可能的N-grams的数量在VN的数量级上，其中V是词汇量，因此考虑到上下文中超过一个 少数单词需要非常大的训练语料库，而N-gram将每个单词视为原子单位，因此它们无法在语义相关的单词序列中进行泛化，而神经语言模型则可以，因为它们将每个单词与实值特征向量相关联，而神经语言模型则可以。N-grams将每个单词视为一个原子单位，因此它们无法在语义相关的单词序列中进行泛化，而神经语言模型则可以，因为它们将每个单词与实值特征的向量相关联，语义相关的单词在该向量空间中最终相互接近。

图4 可视化学习的单词向量
左边是为语言建模而学习的单词表示，非线性地投射到二维的可视化使用t-SNE算法。右边是由英语到法语的编码器-解码器循环神经网络学习的短语的2D表示。可以观察到，语义相似的单词或单词序列被映射到附近的表征上。词的分布式表征是通过使用反向传播来共同学习每个词的表征和预测目标量的函数，如序列中的下一个词或整个翻译词序列。

图5 一个递归神经网络及其前向计算中涉及的计算在时间上的展开
人工神经元，例如，在时间t的节点s下分组的隐藏单元，其值为st，在之前的时间步长中从其他神经元获得输入(这用左边的黑色方块表示，代表一个时间步长的延迟。这样一来，一个递归神经网络可以将一个具有元素xt的输入序列映射成一个具有元素ot的输出序列，每个ot取决于之前所有的xtʹ（对于tʹ≤t）。在每个时间步骤中使用相同的参数。许多其他的架构也是可能的，包括一种变体，在这种变体中，网络可以产生一系列的输出，例如，单词，，每一个输出都被用作下一个时间步的输入。反向传播算法(图1)可以直接应用于右边的展开网络的计算图，计算总误差的导数，例如，生成正确输出序列的对数概率与所有状态st和所有参数的关系。

Recurrent neural networks

When backpropagation was first introduced, its most exciting use was for training recurrent neural networks (RNNs). For tasks that involve sequential inputs, such as speech and language, it is often better to use RNNs (Fig. 5). RNNs process an input sequence one element at a time, maintaining in their hidden units a ‘state vector’ that implicitly contains information about the history of all the past elements of the sequence. When we consider the outputs of the hidden units at different discrete time steps as if they were the outputs of different neurons in a deep multilayer network (Fig. 5, right), it becomes clear how we can apply backpropagation to train RNNs.

RNNs are very powerful dynamic systems, but training them has proved to be problematic because the backpropagated gradients either grow or shrink at each time step, so over many time steps they typically explode or vanish.

Thanks to advances in their architecture and ways of training them, RNNs have been found to be very good at predicting the next character in the text or the next word in a sequence, but they can also be used for more complex tasks. For example, after reading an English sentence one word at a time, an English ‘encoder’ network can be trained so that the final state vector of its hidden units is a good representation of the thought expressed by the sentence. This thought vector can then be used as the initial hidden state of (or as extra input to) a jointly trained French ‘decoder’ network, which outputs a probability distribution for the first word of the French translation. If a particular first word is chosen from this distribution and provided as input to the decoder network it will then output a probability distribution for the second word of the translation and so on until a full stop is chosen. Overall, this process generates sequences of French words according to a probability distribution that depends on the English sentence. This rather naive way of performing machine translation has quickly become competitive with the state-of-the-art, and this raises serious doubts about whether understanding a sentence requires anything like the internal symbolic expressions that are manipulated by using inference rules. It is more compatible with the view that everyday reasoning involves many simultaneous analogies that each contribute plausibility to a conclusion.

Instead of translating the meaning of a French sentence into an English sentence, one can learn to ‘translate’ the meaning of an image into an English sentence (Fig. 3). The encoder here is a deep ConvNet that converts the pixels into an activity vector in its last hidden layer. The decoder is an RNN similar to the ones used for machine translation and neural language modelling. There has been a surge of interest in such systems recently (see examples mentioned in ref. 86).

RNNs, once unfolded in time (Fig. 5), can be seen as very deep feedforward networks in which all the layers share the same weights. Although their main purpose is to learn long-term dependencies, theoretical and empirical evidence shows that it is difficult to learn to store information for very long.*

To correct for that, one idea is to augment the network with an explicit memory. The first proposal of this kind is the long short-term memory (LSTM) networks that use special hidden units, the natural behaviour of which is to remember inputs for a long time. A special unit called the memory cell acts like an accumulator or a gated leaky neuron: it has a connection to itself at the next time step that has a weight of one, so it copies its own real-valued state and accumulates the external signal, but this self-connection is multiplicatively gated by another unit that learns to decide when to clear the content of the memory.

LSTM networks have subsequently proved to be more effective than conventional RNNs, especially when they have several layers for each time step87, enabling an entire speech recognition system that goes all the way from acoustics to the sequence of characters in the transcription. LSTM networks or related forms of gated units are also currently used for the encoder and decoder networks that perform so well at machine translation.

Over the past year, several authors have made different proposals to augment RNNs with a memory module. Proposals include the Neural Turing Machine in which the network is augmented by a ‘tape-like’ memory that the RNN can choose to read from or write to88, and memory networks, in which a regular network is augmented by a kind of associative memory. Memory networks have yielded excellent performance on standard question-answering benchmarks. The memory is used to remember the story about which the network is later asked to answer questions.

Beyond simple memorization, neural Turing machines and memory networks are being used for tasks that would normally require reasoning and symbol manipulation. Neural Turing machines can be taught ‘algorithms’. Among other things, they can learn to output a sorted list of symbols when their input consists of an unsorted sequence in which each symbol is accompanied by a real value that indicates its priority in the list. Memory networks can be trained to keep track of the state of the world in a setting similar to a text adventure game and after reading a story, they can answer questions that require complex inference90. In one test example, the network is shown a 15-sentence version of the The Lord of the Rings and correctly answers questions such as “where is Frodo now?

循环神经网络

当反向传播刚被引入时，它最令人兴奋的用途是训练循环神经网络，即RNNs。对于涉及顺序输入的任务，如语音和语言，通常使用RNNs更好。RNNs每次只处理一个元素的输入序列，在它们的隐藏单元中维护着一个 “状态向量”，它隐含着序列中所有过去元素的历史信息。当我们把隐藏单元在不同离散时间步长的输出看作是深层多层网络中不同神经元的输出时，我们如何应用反向传播来训练RNN就变得很清楚了。

RNNs是非常强大的动态系统，但事实证明，训练它们是有问题的，因为反传播的梯度在每个时间步长或缩小，所以在许多时间步长，他们通常会爆炸或消失。

由于其架构和训练它们的方法的进步，RNNs已经被发现在预测文本中的下一个字符或序列中的下一个单词方面非常出色，但它们也可以用于更复杂的任务。例如，在一次一个单词阅读一个英语句子后，可以训练一个英语 "编码器 "网络，使其隐藏单元的最终状态向量很好地代表了该句子所表达的思想。然后，这个思想向量可以作为联合训练的法语 "解码器 "网络的初始隐藏状态或作为额外的输入，该网络输出法语翻译的第一个单词的概率分布。如果从这个分布中选择一个特定的第一个单词，并作为输入提供给解码器网络，那么它将输出翻译的第二个单词的概率分布，以此类推，直到选择一个完整的停止。总的来说，这个过程是根据一个取决于英语句子的概率分布来生成法语单词的序列。这种相当天真的执行机器翻译的方式已经迅速成为最先进的竞争力，这引起了严重的怀疑，即理解一个句子是否需要像使用推理规则操纵的内部符号表达。它更符合这样的观点，即日常推理涉及许多同时进行的类比，每个类比都为一个结论贡献了可信度。

与其将法语句子的意思翻译成英语句子，不如学习将图像的意思 "翻译 "成英语句子。这里的编码器是一个深度ConvNet，它在最后一个隐藏层中将像素转换为活动向量。解码器是一个类似于机器翻译和神经语言建模的RNN。最近，人们对这种系统的兴趣大增。

RNNs，一旦在时间上展开，可以被看作是非常深的前馈网络，其中所有层共享相同的权重。虽然它们的主要目的是学习长期的依赖关系，但理论和经验证据表明，很难学习存储很长时间的信息。

为了纠正这种情况，一个想法是用显式记忆来增强网络。这种网络的第一个建议是使用特殊隐藏单元的长短期记忆（LSTM）网络，其自然行为是长期记忆输入。一个被称为记忆单元的特殊单元的行为就像一个累加器或一个门控漏电神经元：它在下一个时间步中与自己有一个权重为1的连接，所以它复制自己的实值状态并积累外部信号，但这个自连接被另一个单元乘法门控，它学会决定何时清除记忆内容。

LSTM网络随后被证明比传统的RNN更有效，特别是当它们的每个时间步骤有几个层时，使得整个语音识别系统能够从声学到转录中的字符序列的所有方式。LSTM网络或相关形式的门控单元目前也用于在机器翻译中表现出色的编码器和解码器网络。

在过去的一年里，有几位作者提出了不同的建议，用记忆模块来增强RNNs。这些建议包括神经图灵机和记忆网络，前者通过 "磁带式 "的存储器来增强网络，RNN可以选择从该存储器中读取或写入88，后者通过一种关联存储器来增强常规网络。记忆网络在标准问题回答基准上取得了优异的性能。记忆是用来记忆故事的，以后要求网络回答问题时，就会用到这个故事。

除了简单的记忆之外，神经图灵机和记忆网络正在被用于通常需要推理和符号操作的任务。神经图灵机可以被教会 “算法”。其中，当它们的输入由一个未排序的序列组成时，它们可以学习输出一个排序的符号列表，其中每个符号都伴随着一个表示其在列表中优先级的实际值。记忆网络可以被训练成在类似文字冒险游戏的环境中跟踪世界的状态，在阅读一个故事后，它们可以回答需要复杂推理的问题。在一个测试例子中，网络被展示了15个句子版本的《指环王》，并正确地回答了诸如 "佛罗多现在在哪里？"等问题。

The future of deep learning

Unsupervised learning had a catalytic effect in reviving interest in deep learning, but has since been overshadowed by the successes of purely supervised learning. Although we have not focused on it in this Review, we expect unsupervised learning to become far more important in the longer term. Human and animal learning is largely unsupervised: we discover the structure of the world by observing it, not by being told the name of every object.

Human vision is an active process that sequentially samples the optic array in an intelligent, task-specific way using a small, high-resolution fovea with a large, low-resolution surround. We expect much of the future progress in vision to come from systems that are trained end-toend and combine ConvNets with RNNs that use reinforcement learning to decide where to look. Systems combining deep learning and reinforcement learning are in their infancy, but they already outperform passive vision systems99 at classification tasks and produce impressive results in learning to play many different video games.

Natural language understanding is another area in which deep learning is poised to make a large impact over the next few years. We expect systems that use RNNs to understand sentences or whole documents will become much better when they learn strategies for selectively attending to one part at a time.

Ultimately, major progress in artificial intelligence will come about through systems that combine representation learning with complex reasoning. Although deep learning and simple reasoning have been used for speech and handwriting recognition for a long time, new paradigms are needed to replace rule-based manipulation of symbolic expressions by operations on large vectors.

深度学习的未来

无监督学习在恢复人们对深度学习的兴趣方面起到了催化作用，但后来被纯监督学习的成功所掩盖。虽然我们在这篇评论中没有关注它，但我们预计无监督学习在长期内会变得更加重要。人类和动物的学习在很大程度上是无监督的：我们通过观察世界来发现世界的结构，而不是通过被告知每个物体的名称。

人类的视觉是一个主动的过程，它以一种智能的、特定任务的方式，使用一个小的、高分辨率的蜂窝和一个大的、低分辨率的环绕，对视阵进行顺序采样。我们预计未来视觉领域的大部分进展将来自于端到端的训练系统，并将ConvNets与RNNs结合起来，使用强化学习来决定看哪里。结合深度学习和强化学习的系统还处于起步阶段，但它们已经在分类任务上优于被动视觉系统，并在学习玩许多不同的视频游戏方面产生了令人印象深刻的结果。

自然语言理解是另一个领域，深度学习将在未来几年内产生巨大影响。我们预计，当使用RNNs理解句子或整个文档的系统学习，到每次有选择地参加一个部分的策略时，它们将变得更好。

最终，人工智能的重大进展将通过结合表征学习和复杂推理的系统来实现。虽然深度学习和简单推理已经在语音和手写识别中使用了很长时间，但需要新的范式来取代基于规则的符号表达式操作，对大向量进行操作。