我们将介绍另一种拟合度评估方法-基于对齐（Alignment）的拟合度评估方法。

1.背景

上一节我们介绍了基于Token重演的拟合度评估方法，可以通过该方法区分拟合和不拟合的轨迹。该方法易于理解，并且可以有效地实现。但是，该方法存在一定的缺点，直觉上，（1）拟合度值对于极有问题的事件日志来说往往太高。如果有许多偏差，Petri网就会“充满Token”，并随后允许任何行为。（2）该方法也是特定于Petri网的，并且只能在转换后应用于其他表示。此外，（3）如果案例不适合，该方法不会通过模型创建相应的路径。

我们希望将观察到的行为映射到建模的行为上，以提供更好的诊断，并将不匹配的案例与模型联系起来。例如，要计算两个活动之间的平均等待时间，我们不能忽略所有不完全匹配的活动。如果这样做，结果可能会有偏差。因此，引入对齐（Alignmet）是为了克服这些限制。

2.相关案例介绍

2.1 示例事件日志

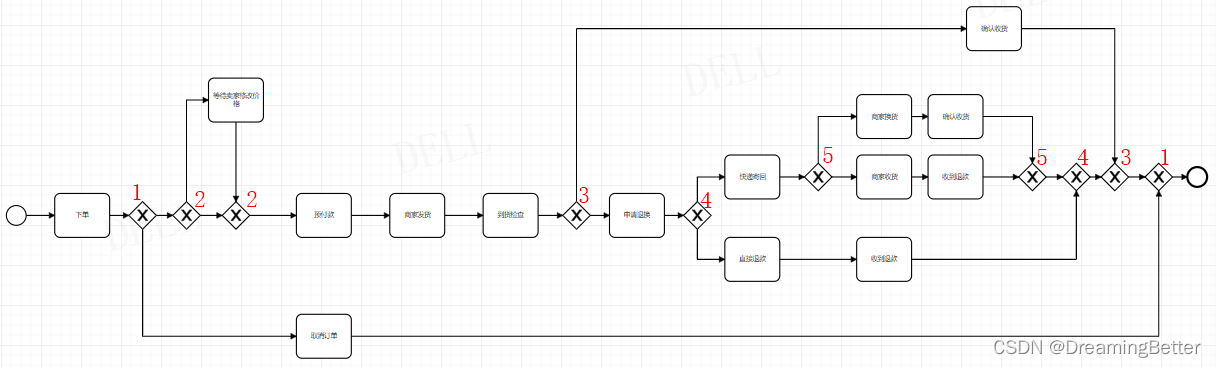
给定一个事件日志L，包含的信息如下表所示，L中共有1391条轨迹，21条轨迹变体（不重复的轨迹数）。例如，在轨迹1=<a,c,d,e,h>中有455个案例，在轨迹2=<a,b,d,e,g>中有191个案例等。

2.2 示例流程模型

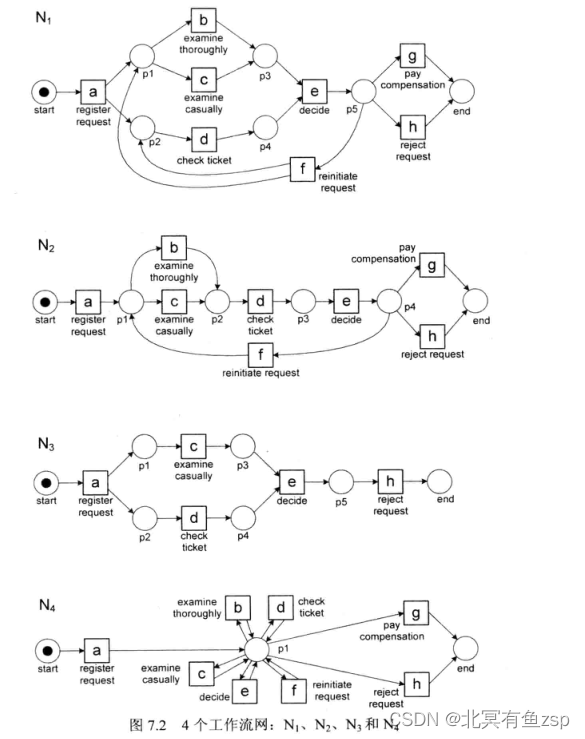
给定四个对应的流程模型，如下图所示，各Petri网模型的具体情况如下所示：

3. 基于对齐的拟合度评估方法

3.1 对齐的概念引入

为了解释对齐的概念，考虑轨迹 $\sigma =\left \langle a,d,b,e,h \right \rangle$ 和之前的四个模型，容易得出，轨迹 $\sigma$ 在N1和N4上是完全拟合的，但在N2和N3不满足条件。

为此引入了optimal alignment（即最佳对齐方式），用于作为一条轨迹和一个模型的最佳匹配。

1.给定一个 $\sigma =\left \langle a,d,b,e,h \right \rangle$ 和N1的一个最佳对齐方式。

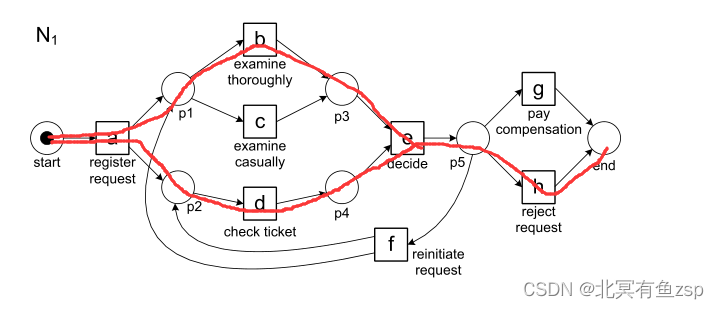
解释：最上面的一行表示事件日志中的轨迹 $\sigma$ ，最下面的一行对应于N1中从初识标识（start）到结束标识(end)的一条路径，也称为模型序列。

2.下面给出轨迹 $\sigma =\left \langle a,d,b,e,h \right \rangle$ 和N2的多条最佳对齐方式。

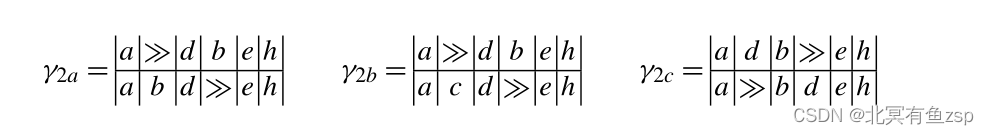
>>表示着未对齐,也意味着无移动。

在 $\gamma$ 2a中，在日志（顶行）和模型（底行）中都可能出现d之前，模型会进行“b移动”，但在日志中无移动。在d之后，日志进行“b移动”，在模型中不再可能。

在γ2b中，模型在d之前进行“c移动”（而不是“b移动”）。

在γ2c中，日志首先进行模型中不可能“d移动”，后和模型一起进行“b移动”，模型再进行“d移动”。

注：所有的三个对齐中都有2个>>（无移动）。

3.给定一个轨迹 $\sigma =\left \langle a,d,b,e,h \right \rangle$ 和N3，这里有三个最优对齐。

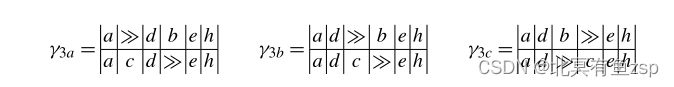
注：模型需要进行“c移动”，日志需要使模型中不可能进行“b移动”。

这些示例说明了对齐的有用性。可以针对每个案例提供详细的诊断，这些诊断可以在流程模型级别聚合为诊断。例如，可以指出一个特定的活动经常被跳过，或者其他一些活动在不应该发生的时候发生。此外，观察到的行为与建模的行为以精确的方式相关。

3.2 基于对齐的拟合度计算

3.2.1 带变迁的对齐引入

当存在重复和静默活动时，基于Token的一致性检查变得更加复杂，例如，使用τ标签的变迁（静默变迁）或使用相同标签的两个变迁（重复活动）。可以为任何流程符号定义对齐，包括具有重复和静默活动的Petri网。为了说明这一点，考虑下图中带有标记Petri网N5，由8个变迁和7个库所组成，变迁t1的标签a为初始注册步骤建模，变迁t2的标签b为检查步骤建模，等等。有两个决策变迁（t4和t5）具有相同的标签d,有一个静默变迁（t6），此变迁为重新初始化步骤建模。正如τ标签所反映的，该步骤是不可见的。

给定σ1=<a, c, d, e>和N5正好有一个最佳对齐。

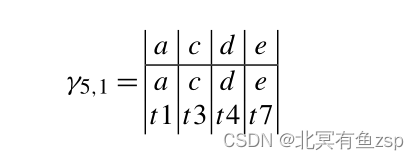
解释：顶部行对应于“日志中的移动”，底部两行对应于“模型中的移动”。 模型中的移动现在由变迁及其标签表示。这是必要的，因为可能有多个具有相同标签的变迁，例如，在t4和t5都有一个 d标签的N5中。记录道σ1中的d事件=<a, c,d,e>表示一个决策，并且与特定的变迁无关。然而，在重演过程中，很明显d必须指t4。

如果日志中的移动无法模拟模型中的移动，则顶行会显示“>>”（“无移动”）。

考虑σ2=<a, b,d,f>，σ2和N5有两种最佳对齐方式：

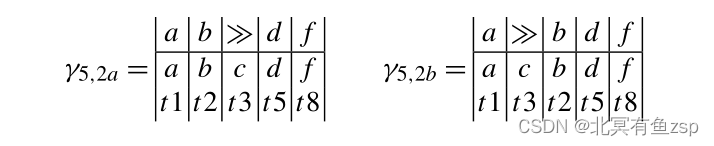
如果模型中的移动无法模拟日志中的移动，则底部一行将显示“<<”（“无移动”）。

考虑σ3=<a, c,d,e,f>，σ3和N5有两种最佳路线：

静默变迁t6在事件日志中不留痕迹。给定σ4=<a,c, d, b, c, d, c, d, c, b, d, f>和N5正好有一个最佳对齐。

解释：对齐循环三次。所有">>"对应于静默变迁t6的模型移动。这些移动被认为是无害的，因为这些移动是不可见的，并且无论如何都无法在日志中观察到。因此，我们认为σ4=<a, c , d, b，c，d，c，d，c，b，d，f>和N5完美拟合。

3.2.2 合法移动（legal move）

move 是一对(x,(y, t))，其中第一个元素指向日志，第二个元素指向模型。

例如，(a，(a，t1)）意味着日志和模型都进行了“移动”，并且模型中的移动是由变迁t1的发生引起的。（>>，（c，t3））意味着标签为c的变迁t3的发生不会被相应的日志移动所模仿。（f，>>）表示日志执行“f移动”，模型后面不跟“f移动”。

发生以下四种情况之一时，则认为（x, (y, t)）是一个合法移动（legal move）：

（1） x=y 且y 是变迁t的可见标签，此时称为同步移动（synchronous move）；

（2）x= >>且y是变迁 t的可见标签，此时称为可见模型移动（visible model move）；

（3）x= >>，y=τ 且变迁 t是沉默的，此时称不可见模型移动（invisible model move）；

（4）x $\neq$ >> ,(y,t) = >> ,此时发生的移动称为日志移动 (log move).

注：此外，其他的移动比如(>>,>>)和(x,(y,t))此时x $\neq$ y都属于不合法移动。

3.2.3 对齐、成本、最佳对齐

对齐(Alignment)是一系列合法的移动，在删除所有>>符号后，首行对应于日志中的轨迹，而底行对应于从流程模型的某个初始状态开始并以某个最终状态结束的触发序列。

给定日志轨迹和流程模型，可能会有许多（如果不是无限多的话）对齐。对于σ2=<a, b, d, f>和N5，还有其他路线，如：

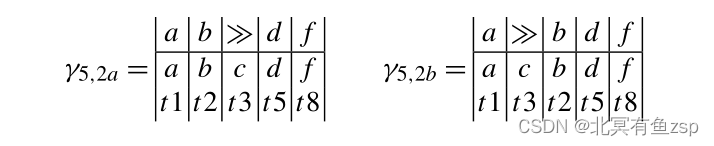
注：对齐γ5,2a和γ5,2b只有一个>>，路线γ5,2c有九个>>，γ5,2d有六个>>。很明显，γ5,2a（或γ5,2b）描述σ2和n5之间的关系比两条较长路线γ5,2c和γ5,2d更好。

为了选择最合适的对齐方式，引入了成本（costs）。将成本(costs)与不需要的移动相关联，并选择总成本最低的对齐方式。成本函数δ将成本分配给合法移动。

成本的几种情况如下：

（1）日志和模型一致的移动没有成本，即δ(x，(y，t))=0，其中该移动为合法的，即x=y。

（2）只有当变迁不可见时，模型中的移动才没有成本，即δ(>>,（τ，t)）=0或不可见的模型移动。

（3）δ(>>,(y,t)) >0 是当模型进行“y移动”而没有相应的日志移动（可见模型移动）时的成本。

（4）δ(x，>>）>0 是仅在日志中“x移动”的成本（日志移动）。

为简单起见，一般情况下，假设一个固定的标准成本函数(standard cost function)，该函数将所有可见的模型移动和日志移动的成本设置为1.比如δ(>>,(y,t)）=δ(x,>>)=1，y $\neq$ τ)

对齐的成本只是其所有移动成本的总和。例如，δ（γ5,2a）=δ（γ5,2b）=1，δ（γ5,2c）=9，δ（γ5,2d）=6。δ（γ5,1）=0表示没有偏差。δ(γ5,4）=0，因为δ(>>,(τ，t6))=0。

如果一个对齐是所有对齐中成本最低的对齐，那么该对齐称为最优对齐（optimal alignmet）。显然，γ5,1和γ5,4是最优的，因为成本为0，不能更低。γ5,2a和γ5,2b是轨迹σ2和模型N5的最佳对准。γ5,3a和γ5,3σ3都和N5是最优对齐。这些示例表明，最优对齐不必是唯一的。

然而，在不丧失一般性的情况下，我们可以假设一个确定性映射，在特定流程模型N的上下文中，将任何日志轨迹σ分配给最优对齐 $\lambda _{opt}^{N}(\sigma )$ 。这种映射有时被称为“Oracle”：对于任何观察到的行为，都会返回通过模型的适当选择路径。

可以将未对准成本转换为介于0（较差的拟合度，即最大成本）和1（完美拟合度，零成本）之间的适应度值。最坏的情况是没有同步移动，只有“仅在模型中移动”和“仅在日志中移动”。请注意，我们始终可以创建一个对齐，其中轨迹σ中的所有事件都转换为日志移动，并将从模型初始状态到最终状态的最短路径添加为模型移动序列。σ2=<a, b, d, f>和N5的“最坏情况对齐”示例是：

最坏情况下的对齐总是产生有效的对齐，并且不可能存在成本较高的最佳对齐, 将此对齐记为 $\lambda _{worst}^{N}(\sigma )$ 。因此，轨迹σ的拟合度可定义如下：

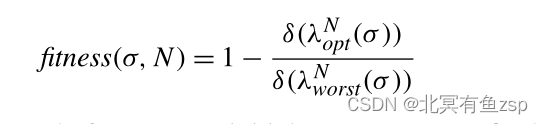
假设有一条从某个初始状态到某个最终状态的路径，这始终会产生一个介于0和1之间的值。对于σ2和模型N5， $\delta (\lambda _{opt}^{N5}(\sigma 2))=1$ ， $\delta (\lambda _{worst}^{N5}(\sigma 2))=8$ ，所以，fitness(σ2，N5）=1−1/8= 0. 875.

同理，拟合度概念可以以一种简单的方式扩展到事件日志，事件日志L和模型N的拟合度计算如下：

其中 $\sum_{\sigma \in L}L(\sigma )\times \delta (\lambda _{opt}^{N}(\sigma ))$ 是使用最优对齐方式重演整个事件日志时所有成本的总和，将其除以最坏情况，以获得标准化的总体拟合度值。

4. 示例

首先考虑第2部分中的示例日志Lfull和模型N1。对于Lfull中的任何轨迹，最佳对齐的成本为0。1391个案例共有7539个同步移动。没有单独的日志或模型移动。因此，fitness（Lfull，N1）=1。

然后，考虑模型N2，此模型不允许并发，并且无法处理d出现在b或c之前的轨迹序列。事件日志Lfull中有457种情况，其中d出现在b或c之前。对于某些轨迹，可以进行多种最佳对齐。这使我们能够使用确定性的“Oracle”返回特定的最佳对齐。Oracle的选择不会影响拟合度计算。根据定义，这些都会产生相同的拟合度值。例如，考虑σ8=<a, c, d, e, f, d, b, e, h>这在Lfull发生了47次。此轨迹的最佳对齐示例如下（省略变迁名称）：

对于Lfull的特定优化路线集合，有7082个同步移动、457个模型移动和457个日志移动。因此， $\sum_{\sigma \in Lfull} L_{full}(\sigma)\times \delta (\lambda _{opt}^{N2}(\sigma ))=457+457=914$ 。Lfull中有7539个事件，从初始标记到最终标记的最短路径需要5个模型移动。因此 $\sum_{\sigma \in Lfull} L_{full}(\sigma)\times \delta (\lambda _{worst}^{N2}(\sigma ))=7539+1391\times 5=14491$ 。这是最糟糕的情况。因此，fitness（Lfull，N2）=1− 914 /14494= 0. 936939。

请注意，拟合度值略低于使用基于Token重演的适应度值。这是由d在b或c之前多次出现（在同一情况下）的情况引起的。使用基于Token的重演不会对这些行为造成足够的惩罚。由于第一次未对准后剩余的标记，在相同情况下未检测到第二次或第三次未对准。

同理，可计算得到Fitness(Lfull，N3）=1−2366 /14494= 0. 83676，fitness(Lfull，N4）=1。

5.工具支持

（1）使用ProM6运行的插件SVN下载地址：https://svn.win.tue.nl/repos/prom/Packages/PNetReplayer/Trunk/

（2）使用pm4py使用对齐的方法计算fitness的链接地址：

PM4Py - Process Mining for Python (fraunhofer.de)

import pm4pyfitness = pm4py.fitness_alignments(log, net, im, fm)

6.总结

使用基于对齐的方法计算拟合度能比基于Token重演方法得到的更精确，但是对于流程模型状态空间较大的情况，还是不容易计算或者效率很慢，为此有许多基于Alignment的改进。

参考文献：

（1）Van Der Aalst W. Process mining: data science in action[M]. Heidelberg: Springer, 2016.

（2）ADRIANSYAH A, MUNOZ-GAMA J, CARMONA J, et al. Alignment based precision checking[C]//International conference on business process management. Berlin, Germany: Springer-Verlag, 2012: 137-149.

基于Token重演的方法和基于Alignment的方法是合规性检查方法中最为重要的两种算法，下一讲我们将对两者进行对比并作总结，依次来更深刻地认识这两种算法。

如需进行相关的了解或者交流，欢迎私信或者加入QQ群：