树增强网络TAN(Tree Augmented Net)
一、为什么要用TAN?
在之前的博客中提到了如何用朴素贝叶斯网络去解决SNS社区虚假账号识别的问题。当时在解决这个问题时,做了如下假设:
- 真实账号比非真实账号平均具有更大的日志密度、更大的好友密度、更多地使用真实头像。
- 日志密度、好友密度和是否使用真实头像在账号真实性给定的条件下是独立的,也就是特征属性之间的独立性。
仔细想想就知道第二条假设是不可能成立的,因为好友密度除了与账号真实性相关之外,还和是否使用真实头像有关。当你使用真实头像的时候,肯定是趋向于吸引更多的人加你为好友,从而拥有更大的好友密度。
所以当“头像是否真实”和“好友密度”之间产生相互关系的时候,简单的NB网络就不再适用了。
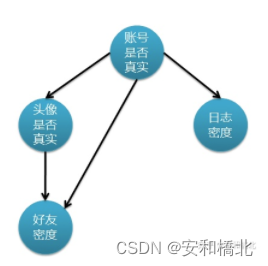
因此,TAN的出现就解决了部分属性之间存在依赖的问题。
在上面的例子中,我们是通过主观意识去判断“头像是否真实”和“好友密度”之间存在依赖关系,但是这样毕竟不够准确。如果机器能够根据我们提供的数据集来帮助我们得出这样的关系就好了,而TAN就可以完成这个工作。
二、互信息MI(mutual information)
在介绍这一重要的概念之前,我们先引入其他三个概念:熵、条件熵、信息增益。
1. 熵
含义
在信息论中,熵是指每条消息中包含的信息平均量,又被称为信息熵。
高中的化学学习让我们知道,熵是衡量一种事物的混乱度的。在此处,我们可以把熵理解为不确定性的度量。也就是说,一件事情的结果越不确定,它的熵就越大。
计算
熵描述的是某个事件的不确定性,如果某个事件有n个结果,每个结果的概率为 P n P_{n} Pn。那么这个事件的熵H定义式就为:
H = − ∑ i = 1 n p i log 2 p i H=-\sum^{n}_{i=1} p_{i}\log_{2} p_{i} H=−i=1∑npilog2pi
相应的可以得出联合熵的计算公式:
H ( X , Y ) = − ∑ x ∈ X ∑ y ∈ Y p ( X , Y ) l o g 2 p ( X , Y ) H\left( X,Y\right) =-\sum^{}_{x\in X} \sum^{}_{y\in Y} p\left( X,Y\right) log_{2}p\left( X,Y\right) H(X,Y)=−x∈X∑y∈Y∑p(X,Y)log2p(X,Y)
例如,假设有一场足球赛,巴西队对战中国队。假设巴西队获胜的概率为 0.9,不胜的概率为 0.1。那么这场比赛结果的熵就是:
H = − ∑ i = 1 n p i log 2 p i = − 0.9 × log 2 0.9 − 0.1 × log 2 0.1 = 0.469 H=-\sum^{n}_{i=1} p_{i}\log_{2} p_{i}=-0.9\times \log_{2} 0.9-0.1\times \log_{2} 0.1=0.469 H=−i=1∑npilog2pi=−0.9×log20.9−0.1×log20.1=0.469
假设有另一场足球赛,英国队对战法国队。假设英国队获胜或不胜的概率都是0.5。那么这场比赛结果的熵就是:
H = − ∑ i = 1 n p i log 2 p i = − 0.5 × log 2 0.5 − 0.5 × log 2 0.5 = 1 H=-\sum^{n}_{i=1} p_{i}\log_{2} p_{i}=-0.5\times \log_{2} 0.5-0.5\times \log_{2} 0.5=1 H=−i=1∑npilog2pi=−0.5×log20.5−0.5×log20.5=1
后者的熵比前者的大,由此可见结果的不确定性更大,所以比赛结果的信息量就更大。
2. 条件熵
熵是对事件结果不确定性的度量,但是在某些条件下,这个不确定性会变小。
条件熵和条件概率的概念差不多,它衡量的就是在某个条件X下,事件Y的不确定性,记作
H ( Y ∣ X ) = ∑ x ∈ X p ( x ) H ( Y ∣ X = x ) = − ∑ x ∈ X ∑ y ∈ Y p ( x , y ) l o g 2 p ( y ∣ x ) H\left( Y|X\right) =\sum^{}_{x\in X} p\left( x\right) H(Y|X=x)=-\sum^{}_{x\in X} \sum^{}_{y\in Y} p\left( x,y\right) log_{2}p\left( y|x\right) H(Y∣X)=x∈X∑p(x)H(Y∣X=x)=−x∈X∑y∈Y∑p(x,y)log2p(y∣x)
3. 信息增益
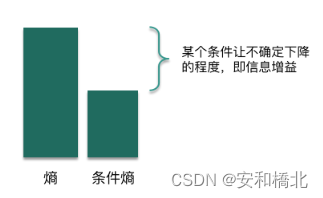
由上述可知,熵是衡量事件的不确定性;条件熵是衡量在已知某个条件后,该事件的不确定性。
对于同一个事件,熵的值肯定是大于等于条件熵的值的,所以引出了信息增益的概念,也就是我们说的互信息量mutual information。
对于信息增益,我们可以理解为:引入了某个条件后,提供了一定的信息,让这件事情的不确定性下降了,而下降的程度就是信息增益。
它的计算方式为熵减去条件熵:
I ( X , Y ) = H ( Y ) − H ( Y ∣ X ) = H ( X ) − H ( X ∣ Y ) I\left( X,Y\right) =H\left( Y\right) -H\left( Y|X\right) =H\left( X\right) -H\left( X|Y\right) I(X,Y)=H(Y)−H(Y∣X)=H(X)−H(X∣Y)
同时也等于:
I ( X , Y ) = H ( X ) + H ( Y ) − H ( X , Y ) I\left( X,Y\right) =H\left( X\right) +H\left( Y\right) -H(X,Y) I(X,Y)=H(X)+H(Y)−H(X,Y)
4. 互信息
互信息描述的是两个随机变量间相互依赖的程度,用 I ( X , Y ) I\left( X,Y\right) I(X,Y)表示,它度量两个随机变量共享的信息——知道随机变量X,对随机变量Y的不确定性减少的程度(或者知道随机变量Y,对随机变量X的不确定性减少的程度)。
用venn图表示互信息与熵、条件熵之间的关系如下所示:
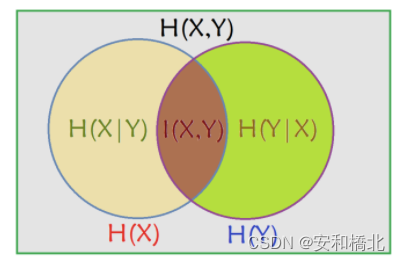
通过上述熵、条件熵以及互信息的计算方法,可以推出:
若 ( X , Y ) ∼ p ( x , y ) \left( X,Y\right) \sim p\left( x,y\right) (X,Y)∼p(x,y),则X, Y之间的互信息 I ( X , Y ) I\left( X,Y\right) I(X,Y)定义为:
I ( X , Y ) = ∑ x ∈ X ∑ y ∈ Y p ( X , Y ) log 2 p ( X , Y ) p ( X ) p ( Y ) I\left( X,Y\right) =\sum^{}_{x\in X} \sum^{}_{y\in Y} p\left( X,Y\right) \log_{2} \frac{p\left( X,Y\right) }{p\left( X\right) p\left( Y\right) } I(X,Y)=x∈X∑y∈Y∑p(X,Y)log2p(X)p(Y)p(X,Y)
5. 举例
血型与皮肤癌
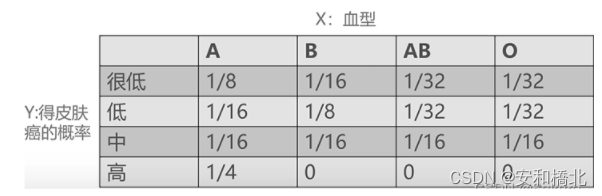
横轴代表血型,纵轴代表得皮肤癌的概率,上述是两者的联合概率分布表。

0.375这个值表示,当知道了一个人的血型X之后,对于得皮肤癌的概率Y这个随机变量的不确定性减少了0.375。也就是说,在知道了血型之后,或多或少的就知道了这个人患上皮肤癌的概率信息。