MI相关--学习笔记

MI（mutual information）：
1. 基于互信息的donsker-varadhan下界，则使用神经网络来估计互信息就转化为了一个优化问题，可以通过梯度上升算法来实现。
2. 互信息可以看做加强版的 correlation，correlation 只能反映变量之间的线性关系，但是互信息可以进一步反映变量之间的非线性关系；这一点在量化金融里面也非常有用。
3. 给定一堆相互关联的数据 x 和 z，需要给出这两组数据之间互信息的估计。方法就是训练一个神经网络（statistic network） T，训练目标就是对 Donsker-Varadhan 下界做梯度上升，最后的估计值就是 Donsker-Varadhan 下界在样本上的估计。
4. 仅仅找出两组数据之间的互信息看起来也并不是特别有用。但是很多应用中会把互信息放入目标函数中，可以使用如下的 statistic network 来得到目标函数相对于输入（x 或者 z）的导数，从而完成梯度的传递。
5. 互信息可以表示为 KL 散度，而 KL 散度可以写出 Donsker-Varadhan 表示形式；可以看出对于任意的如果目标是 E[f(.)]（比如E[log(.)] ）对应的随机梯度算法都是真实梯度的无偏估计；但是这里的目标是 f(E[.])，因此无法得到一个无偏的梯度估计（考虑 Jensen 不等式）。一个 T函数，都对应了互信息的一个下界。
MINE：mutual information neural estimator互信息神经网络估计器
1. 应用gan：
  1. GAN 有一个问题是 mode-dropping，简单说来就是，生成器很容易只学习到一种能够有效“欺骗”判别器的模式；这样生成器生成出来的数据（比如图片）看起来很真，但是它只会生成这一种（比如实际图片分布有各种图片，但是生成器最后只会生成包含狗的图片）。这里的做法就是把 z 分为两个部分 z=[e,c]，然后同时最大化生成图片和 c 之间的互信息。这相当于要求生成的图片尽可能反映 c 的信息（比如给定的 c 如果是某个数字，那么 G 就生成狗；如果是另外的数字，G 就生成猫）。
  2. 通过MINE 方法，可以有效地对于互信息这一项关于 G 求导。实验结果表明，这种方法对应生成出来的数据点更能够有效覆盖整体的原始数据分布。
2. 应用：Reconstruction（bi-directional adversarial models）仍然考虑 GAN 类似的网络结构，不过现在加入一个 reverse model F。任务目标是给定一个图片（可能被污染了），重构出来这张图片。一个最明显的目标就是最小化重构误差
3. 应用：Information Bottleneck：Information bottleneck 的目标是找到 x 的一个好的表示，使得这个表示比较 compact 但是也能够很好的预测另外一个变量 y。经过推导，可以得到相应的目标函数，目标函数包含互信息项目。

信息论相关量之间的关系：

文氏图：
1. area：信息的数量
2. relationship：加减关系
3. 左圈H(x)，右圈H（y）,左右两个圈H（x,y）

定义：

extropy：H_p=H(x)=-Σ_x p（x）logp（x）joint extropy：H（x,y）=-Σ_x,y p（x，y）logp（x,y）conditional extropy: H（x,y）=-Σ_x,y p（x，y）log[p（x,y）/p(x)]mutual information:l（x,y）=-Σ_x,y p（x，y）log[p（x,y）/(p(x)p(y))]=D_KL  (p(x,y) || p(x)p(y) )KL 散度（relative entropy）：D_KL (p||q) =-Σ_xp（x）log[q(x)/p(x)]交叉熵：H（p,q）=-Σ_xp（x）log[q(x)]=D_KL (p||q)+H_p

MI相关--学习笔记

相关文章

NVMe-MI协议解读

MIMO是什么

百度一款前端图片合成工具库MI开源啦！

解决cas aba的问题解决方案–AtomicStampedReference的引用加版本号

数据结构-归并排序：理解和实现（附C++代码）

20230524 taro+vue3+webpack5+pdfjs时打包pdfjs进不来的问题

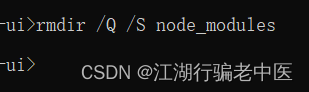
windows 快速删除node_modules文件夹

工具篇6--kafka消息模型介绍