文章目录
- 一、相机标定
- 二、径向畸变
- 1.桶状畸变
- 2.枕形畸变
- 三、角点检测
- 1.MATLAB R2020a
- 2.PyCharm+opencv
一、相机标定
相机标定方法有:传统相机标定法、主动视觉相机标定方法、相机自标定法、零失真相机标定法。
这是一个针孔相机模型

C 点表示camera centre,即相机的中心点,也是相机坐标系的中心点;
Z 轴表示principal axis,即相机的主轴;
p 点所在的平面表示image plane,即相机的像平面,也就是图片坐标系所在的二维平面;
p 点表示principal point,即主点,主轴与像平面相交的点;
C 点到 p 点的距离,也就是右边图中的 f 表示focal length,即相机的焦距;
像平面上的 x 和 y 坐标轴是与相机坐标系上的 X 和 Y 坐标轴互相平行的;
相机坐标系是以 X , Y , Z 三个轴组成的且原点在 C 点,度量值为米(m);
像平面坐标系是以 x ,y 两个轴组成的且原点在 p 点,度量值为米(m);
图像坐标系一般指图片相对坐标系,在这里可以认为和像平面坐标系在一个平面上,不过原点是在图片的角上,而且度量值为像素的个数(pixel);
引入内参
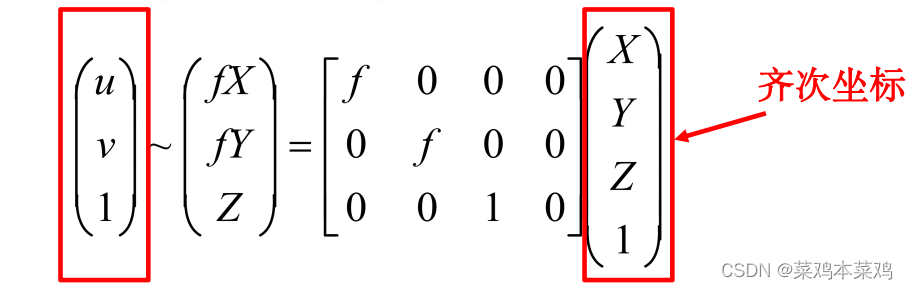
引入齐次坐标的原因 原因
二、径向畸变
什么是径向畸变?
随着道路监控摄像机和车载摄像机在日常生活中的广泛应用,人们对摄像机能够监控到的范围提出了新的更高的要求,因此广角镜头也必将越来越多出现在实际的应用当中。然而,广角镜头获取到的图像会产生明显的径向畸变,不符合人们的视觉习惯,并且畸变会对依赖图像相关信息进行的空间定位、目标跟踪等的算法产生十分严重的影响,可能会导致其结果存在非常严重的错误。在计算机视觉领域的其他方向,图像的畸变也会对其后续的图像处理算法产生难忽视的影响。
畸变分为径向畸变,切向畸变:
在图像的各种形式的畸变中,图像径向畸变占据着主导地位,图像的径向畸变包括两种:桶形畸变和枕形畸变。通常情况下,成像过程中短焦距镜头产生桶形畸变,长焦距镜头产生枕形畸变。另外种畸变是切向畸变,但是在实际的相机中几乎不会引入明显的切向畸变。
图像径向畸变原因:
①透镜质量原因
②光线在远离透镜中心的地方比靠近中心的地方更加弯曲
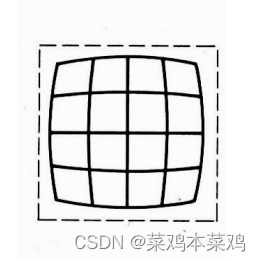
1.桶状畸变
桶状变形(Barrel Distortion)亦可称为负变形(Negative distortion),这是一种成像缺陷。桶状变形的影像像点会随着与中心点距离之增大而移位。令影像中的“直线”中段向外弯曲,两端则向中心弯曲变成“曲线”。所以,方形物体的影像会变成四角向内收缩,边线中段则向外凸出,好像一个木桶,因此被称为桶状变形。
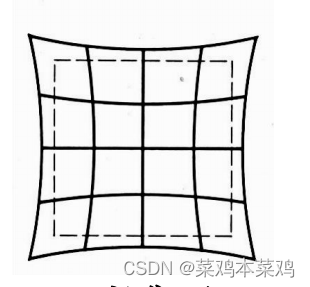
2.枕形畸变
枕状变形在照片中会比较少用,但桶状变形的应用层面则广得多,原因是桶状变形往往能带出夸张有趣的效果,比如我们经常看到的“大头”效果,之前红极一时的”大头”效果其实也是桶状变形的一个应用,拍摄”大头”照片时,最好使用鱼眼镜头,它是一种超广角镜头,焦距可以达10mm,用它能够突出效果,并由高处近距离拍摄来做成头大身细的夸张效果。
三、角点检测
用的是12*9的棋盘格,取了13张不同角度的照片。
1.MATLAB R2020a
执行步骤

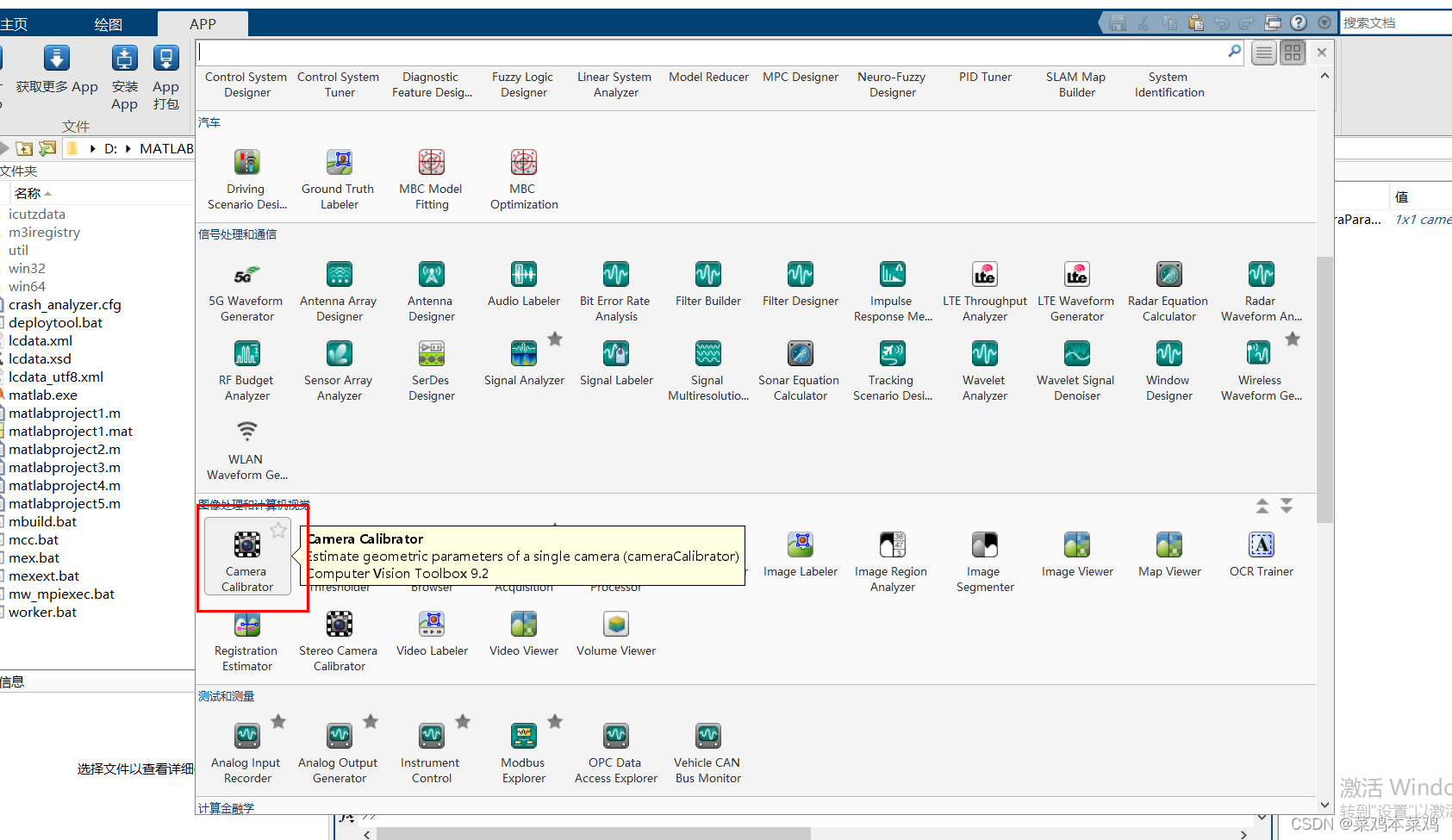
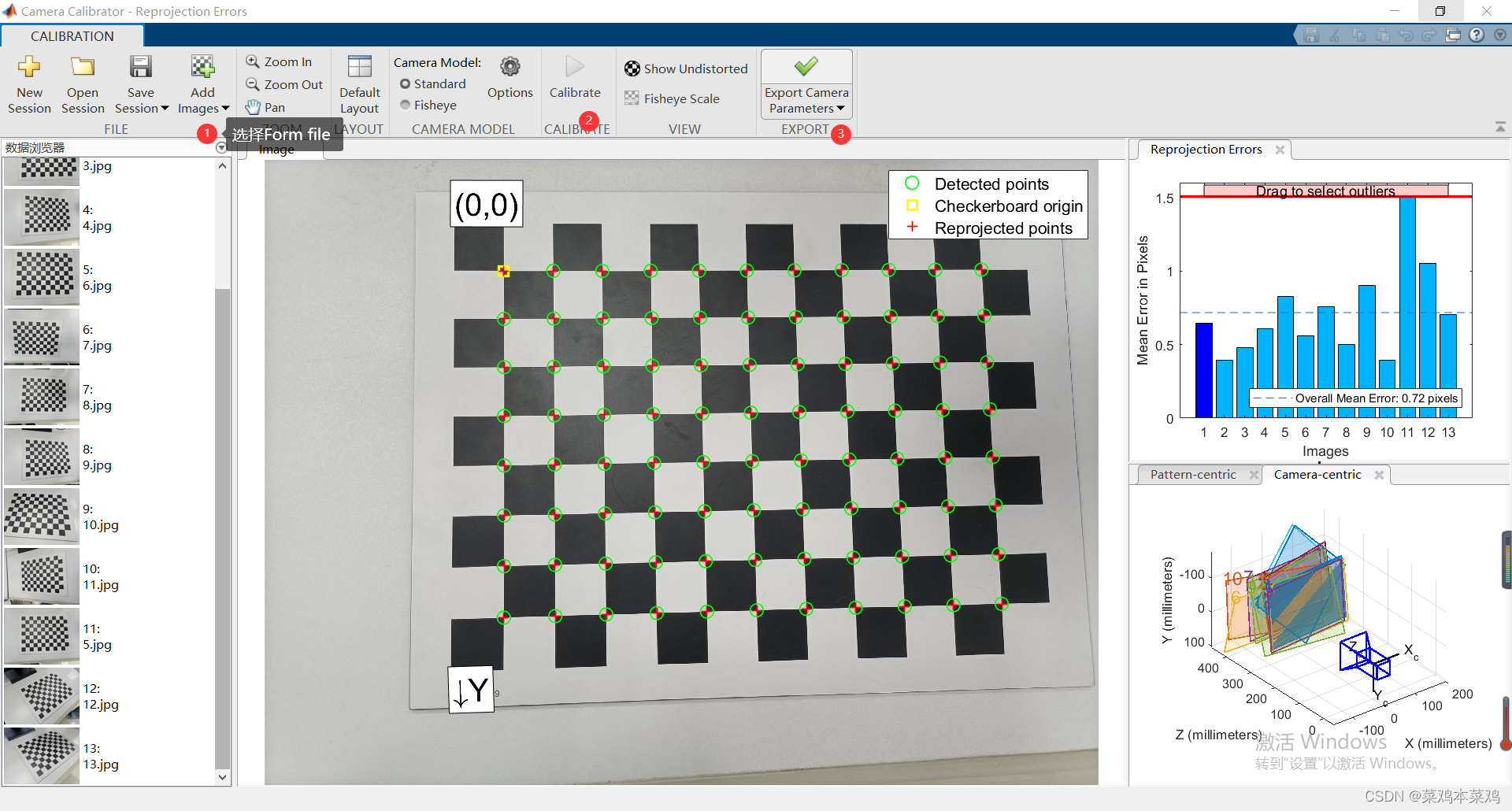
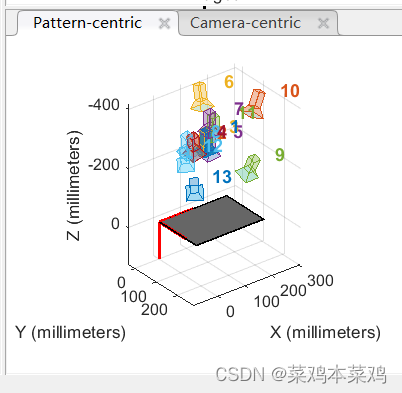
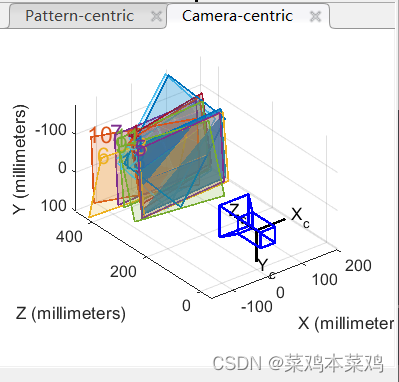
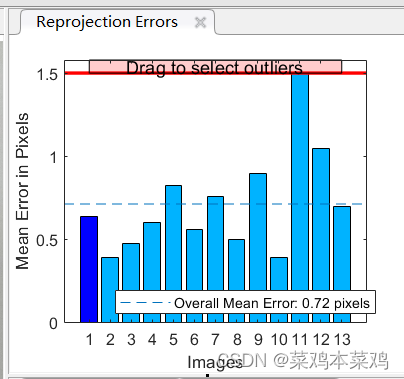
在matlab工作空间里可以看到相机参数的属性
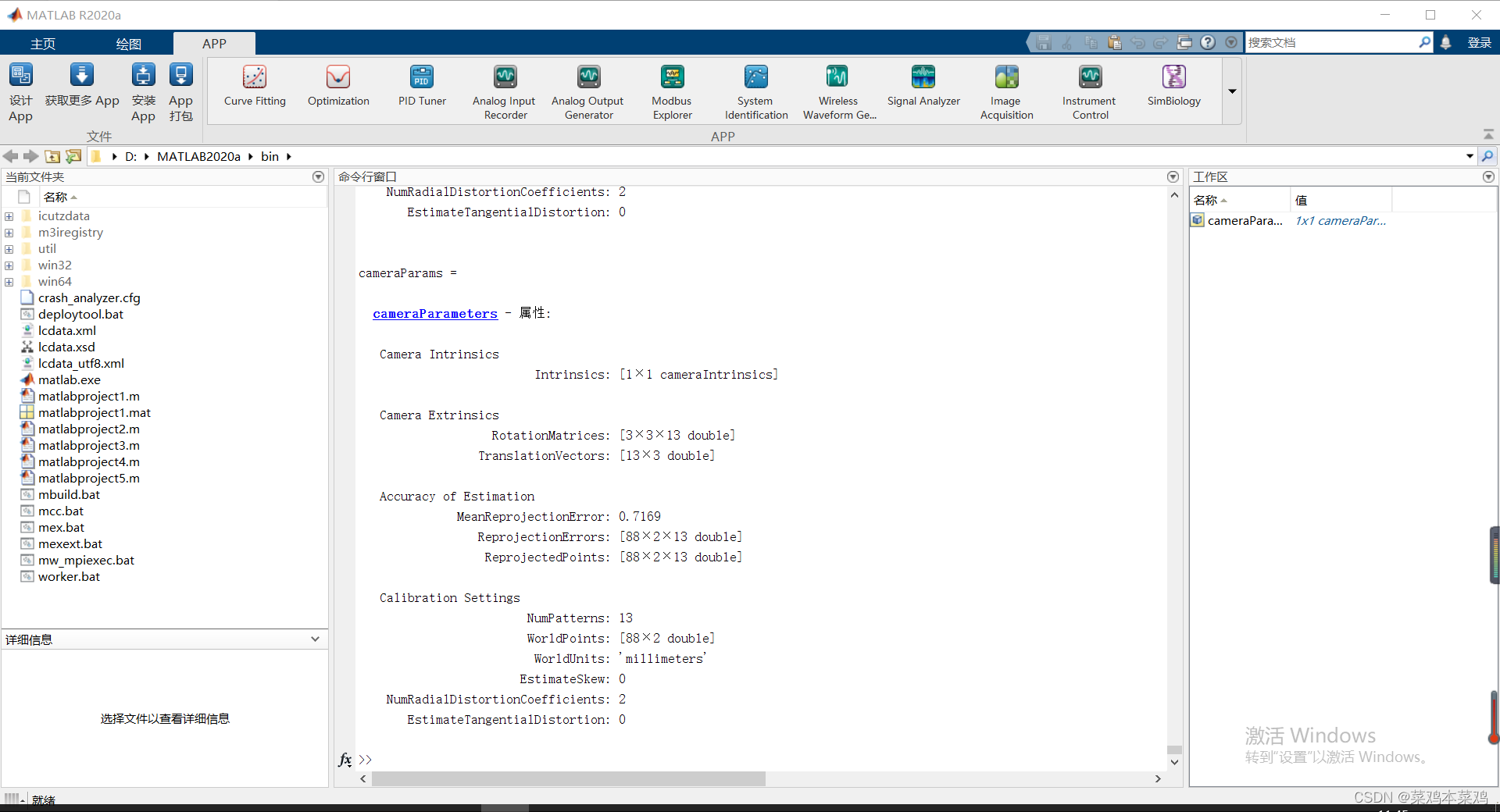
2.PyCharm+opencv
import cv2
import glob
import numpy as np#棋盘规格
cbraw = 11
cbcol = 8
# prepare object points, like (0,0,0), (1,0,0), (2,0,0) ....,(6,5,0)
objp = np.zeros((cbraw*cbcol,3), np.float32)
'''
设定世界坐标下点的坐标值,因为用的是棋盘可以直接按网格取;
假定棋盘正好在x-y平面上,这样z=0,简化初始化步骤。
mgrid把列向量[0:cbraw]复制了cbcol列,把行向量[0:cbcol]复制了cbraw行。
转置reshape后,每行都是9*11网格中的某个点的坐标。
'''
objp[:,:2] = np.mgrid[0:cbraw,0:cbcol].T.reshape(-1,2)objpoints = [] # 3d point in real world space
imgpoints = [] # 2d points in image plane.
#glob是个文件名管理工具
images = glob.glob("D:/PyCharmProjects/Forth/images/*.jpg")
for fname in images:
#对每张图片,识别出角点,记录世界物体坐标和图像坐标img = cv2.imread(fname) #source image#我用的图片太大,缩小了一半img = cv2.resize(img,None,fx=0.5, fy=0.5, interpolation = cv2.INTER_CUBIC)gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY) #转灰度#cv2.imshow('img',gray)#cv2.waitKey(1000)#寻找角点,存入corners,ret是找到角点的flagret, corners = cv2.findChessboardCorners(gray,(11,8),None)#criteria:角点精准化迭代过程的终止条件criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)#执行亚像素级角点检测corners2 = cv2.cornerSubPix(gray,corners,(11,11),(-1,-1),criteria)objpoints.append(objp)imgpoints.append(corners2)#在棋盘上绘制角点,只是可视化工具img = cv2.drawChessboardCorners(gray,(11,9),corners2,ret)cv2.imshow('img',img)#cv2.waitKey(1000)
'''
传入所有图片各自角点的三维、二维坐标,相机标定。
每张图片都有自己的旋转和平移矩阵,但是相机内参和畸变系数只有一组。
mtx,相机内参;dist,畸变系数;revcs,旋转矩阵;tvecs,平移矩阵。
'''
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, gray.shape[::-1],None,None)
img = cv2.imread('D:/PyCharmProjects/Forth/images/1.jpg')
#注意这里跟循环开头读取图片一样,如果图片太大要同比例缩放,不然后面优化相机内参肯定是错的。
img = cv2.resize(img,None,fx=0.5, fy=0.5, interpolation = cv2.INTER_CUBIC)
h,w = img.shape[:2]
'''
优化相机内参(camera matrix),这一步可选。
参数1表示保留所有像素点,同时可能引入黑色像素,
设为0表示尽可能裁剪不想要的像素,这是个scale,0-1都可以取。
'''
newcameramtx, roi=cv2.getOptimalNewCameraMatrix(mtx,dist,(w,h),1,(w,h))
#纠正畸变
dst = cv2.undistort(img, mtx, dist, None, newcameramtx)#输出纠正畸变以后的图片
x,y,w,h = roi
dst = dst[y:y+h, x:x+w]
cv2.imwrite('Ex4result.png',dst)
#打印我们要求的两个矩阵参数
print ("newcameramtx:\n",newcameramtx)
print ("dist:\n",dist)
#计算误差
tot_error = 0
for i in range(len(objpoints)):imgpoints2, _ = cv2.projectPoints(objpoints[i], rvecs[i], tvecs[i], mtx, dist)error = cv2.norm(imgpoints[i],imgpoints2, cv2.NORM_L2)/len(imgpoints2)tot_error += errorprint ("total error: ", tot_error/len(objpoints))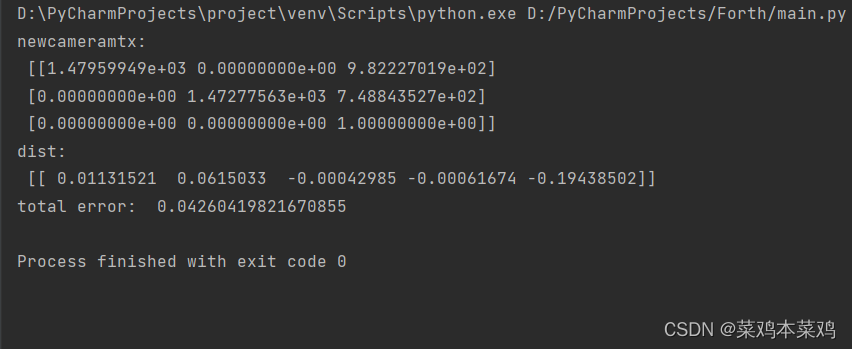
由上图我们就可以知道mtx,相机内参;dist,畸变系数;



