一、算法类别

        BMS中所采用的算法类别主要有：安时积分、开路电压测量、人工神经网络、卡尔曼滤波四中方案。其中安时积分法是主体算法，但是由于器件精度、采集误差、计算误差、累积误差、电池充放曲线非线性等各种原因，需要一些辅助修正算法（后三种），才能将SOC计算得相对准确一些。

二、安时积分估算原理

        SOC：表示电池的剩余容量占比，即SOC = 

           其中Qmax是电池系统的标称容量，Q是电池剩余电量。

Qmax作为标称容量，初始值是定死的，但在后续电池使用中也不是一成不变的，主要因为电池受到温度、老化等影响，容量会衰减变化。故有几种修正策略：

1、依据电池实验数据，查表得出当前电池经历了多少循环，对应的实际标称容量是多少。

2、如果有SOH（可以通过检测电池内阻再查表得出SOH），标称容量*SOH =实际容量。

3、充放守恒，例：充电量+剩余电量 =放电量。

4、每次充满或放完都要对Qmax进行修正。

5、以上都要结合温度情况进行参数修正。

Q是电池剩余电量，通过 得出，一般充电为正，放电为负。

SOC（init)是初始SOC值，出厂前可根据电池剩余容量比进行初值标定，之后就按照实际剩余容量进行赋值。

1、安时积分算法本身依赖SOC的初始值，故SOC（init)一定要正确。--标定、修正

2、要尽量保证充放首末端的SOC变化趋势不突兀。--SOC变化速率分段式线性化。

3、会受电流采样精度、温漂等因素影响结果。--EKF

4、计算误差和采样误差等会越来越大，这些累积误差要通过修正策略弥补。-OCV+EKF+策略

三、安时积分基础部分的实现

       先来个积分的例子，在没有发现圆面积公式之前，巨人们都是这样计算的：把一个圆沿圆心切割成多个扇形，每个扇形近似看作一个等腰三角形，把这些三角形面积累加起来就是圆的面积，分割的扇形越多，计算出来的圆面积越接近真实。

        安时积分估算SOC和求圆面积的原理是一样的，例如有一组容量为100Ah的电池，即能够以100A的电流放电1小时，假如50A电流放电一小时，那么SOC就是50%，但是电流不可能恒定，所以把电流按时间轴分割成若干份，每一份的时间宽度根据硬件采样频率来设定，那么，采样时间越快，SOC估算精度就越高。

        实现方式 : 包含3个参数：SOC初值、电池系统额定设计容量、电流采样值。

 

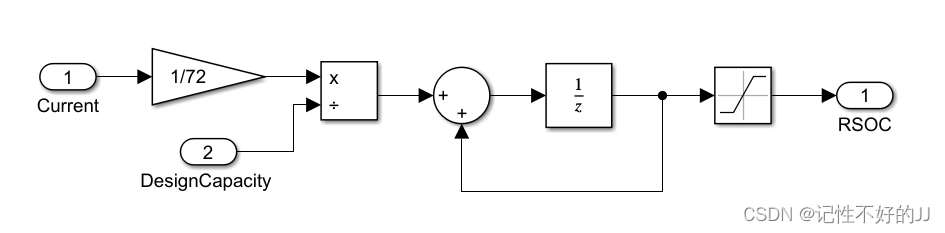
           Current是采样的电流值，DesignCapacity 是电池的初始容量，暂不考虑老化温度等因素，此处采用常数代替。增益代表时间，由于这里是0.5S的定步长，所以1小时采样7200次，可以根据实际电流采样频率去设定。

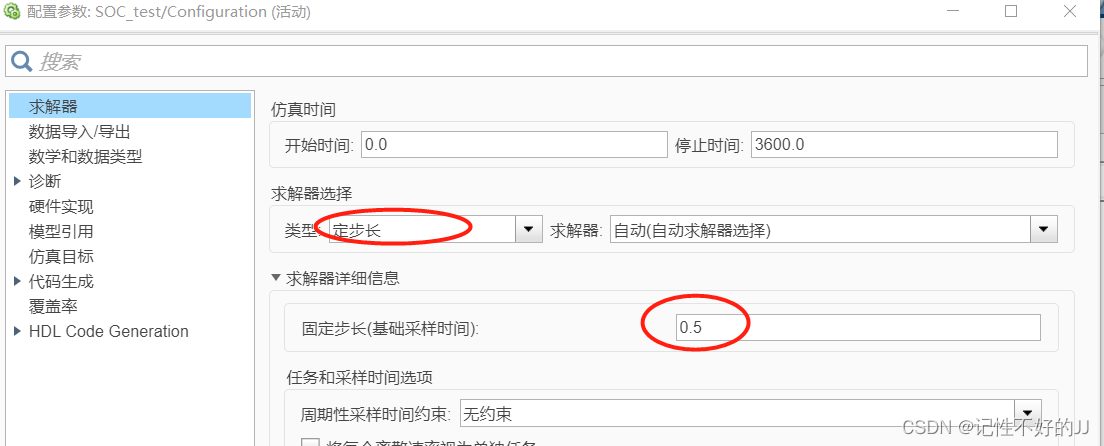
       举例：100Ah的电池，电流采样频率2HZ，假如某一时刻采样值100A，那么它占了整个放电时间的  .

        之后是用求和模块和延时模块组成的累积和，最后用初始的比例值减去累积的比例就是剩余电量的比例。

        简单仿真一下：

 

 

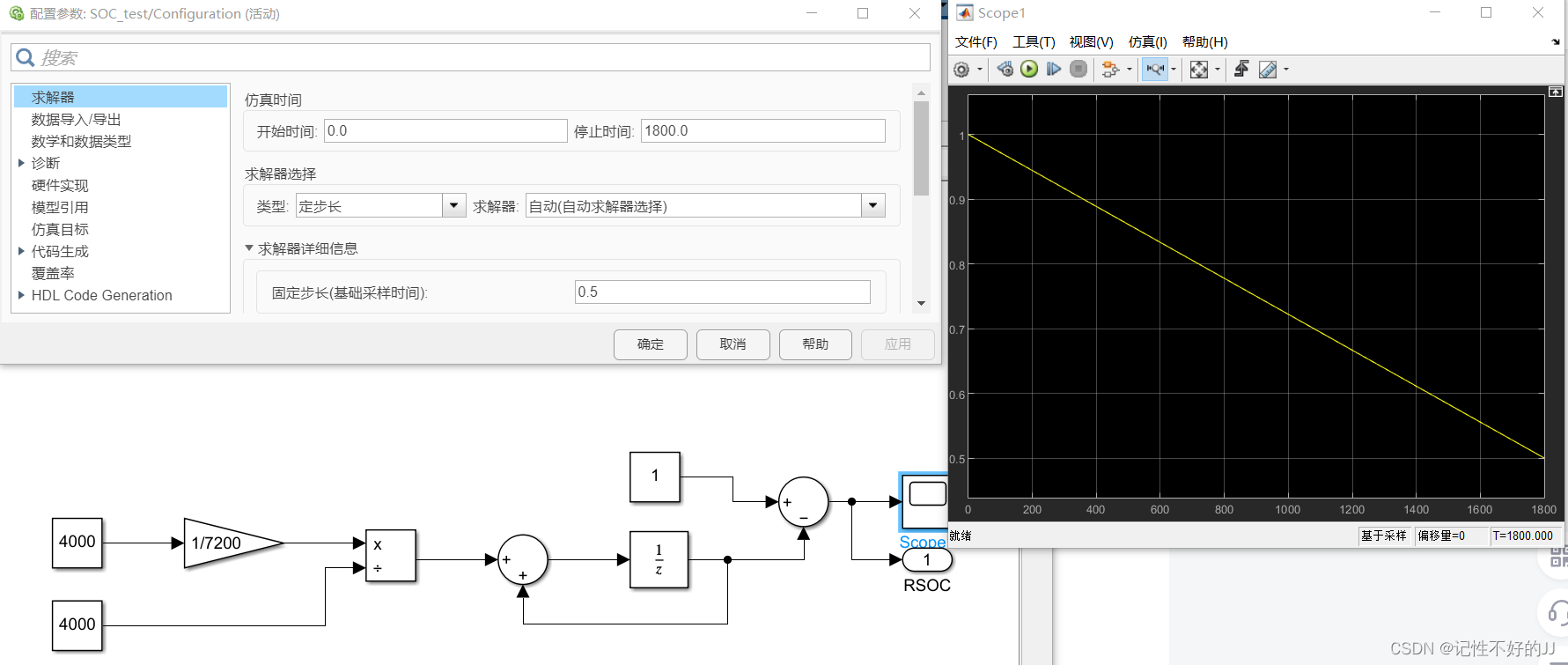
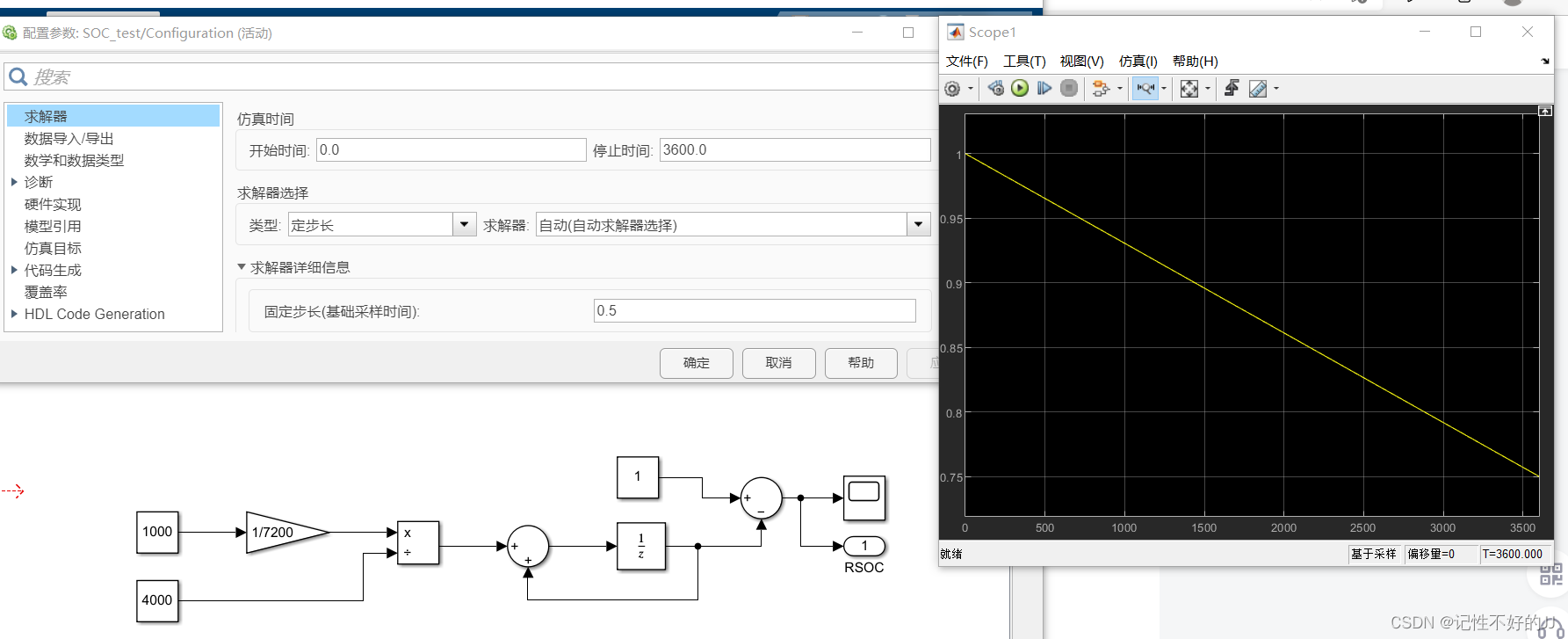
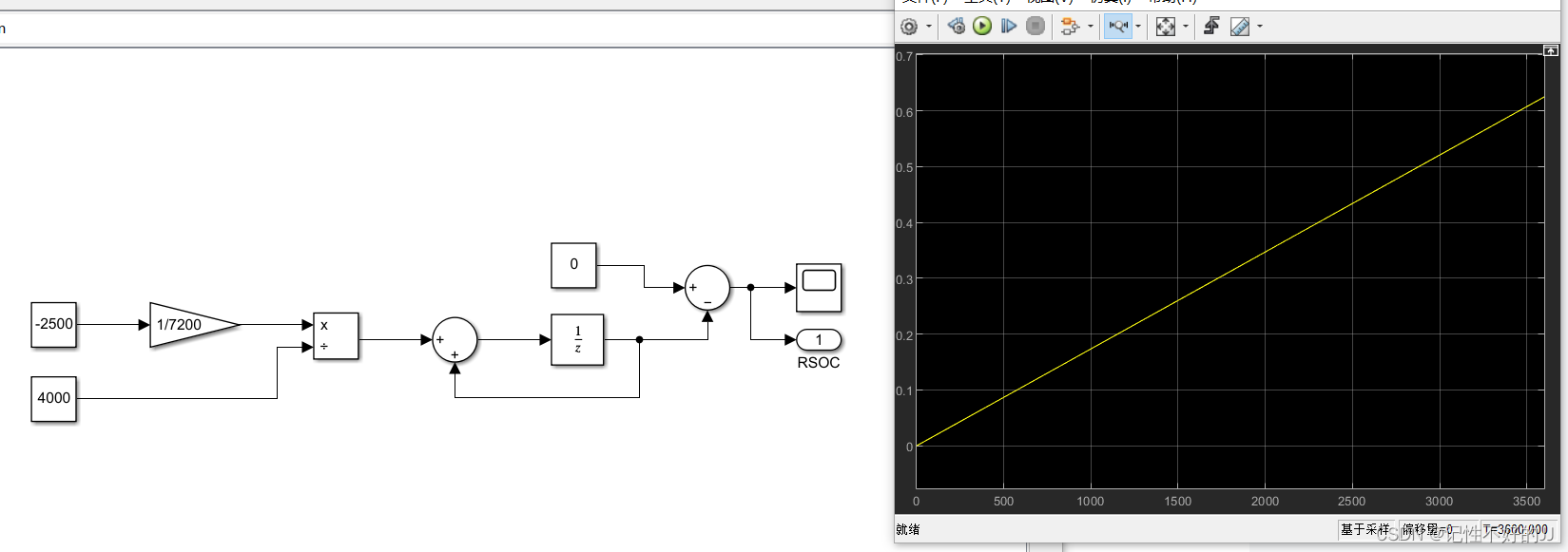
 生成代码测试一下：

 

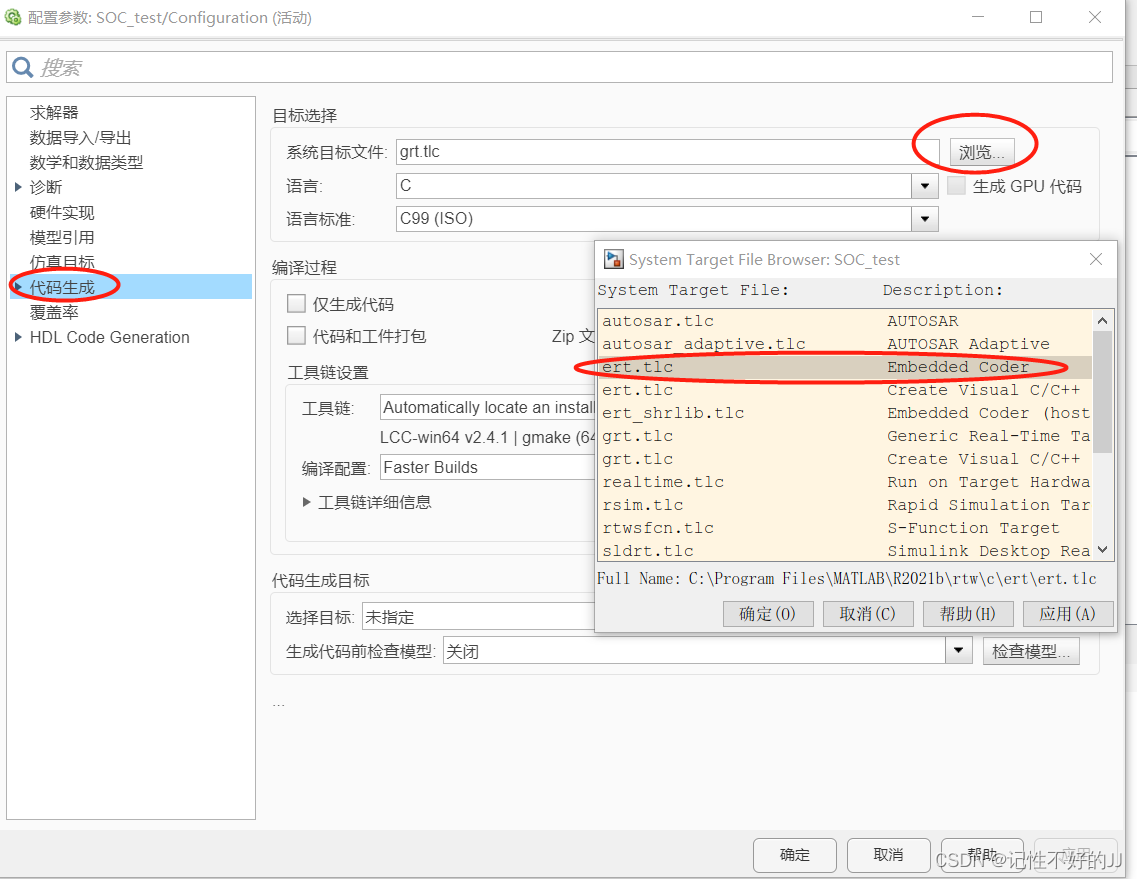
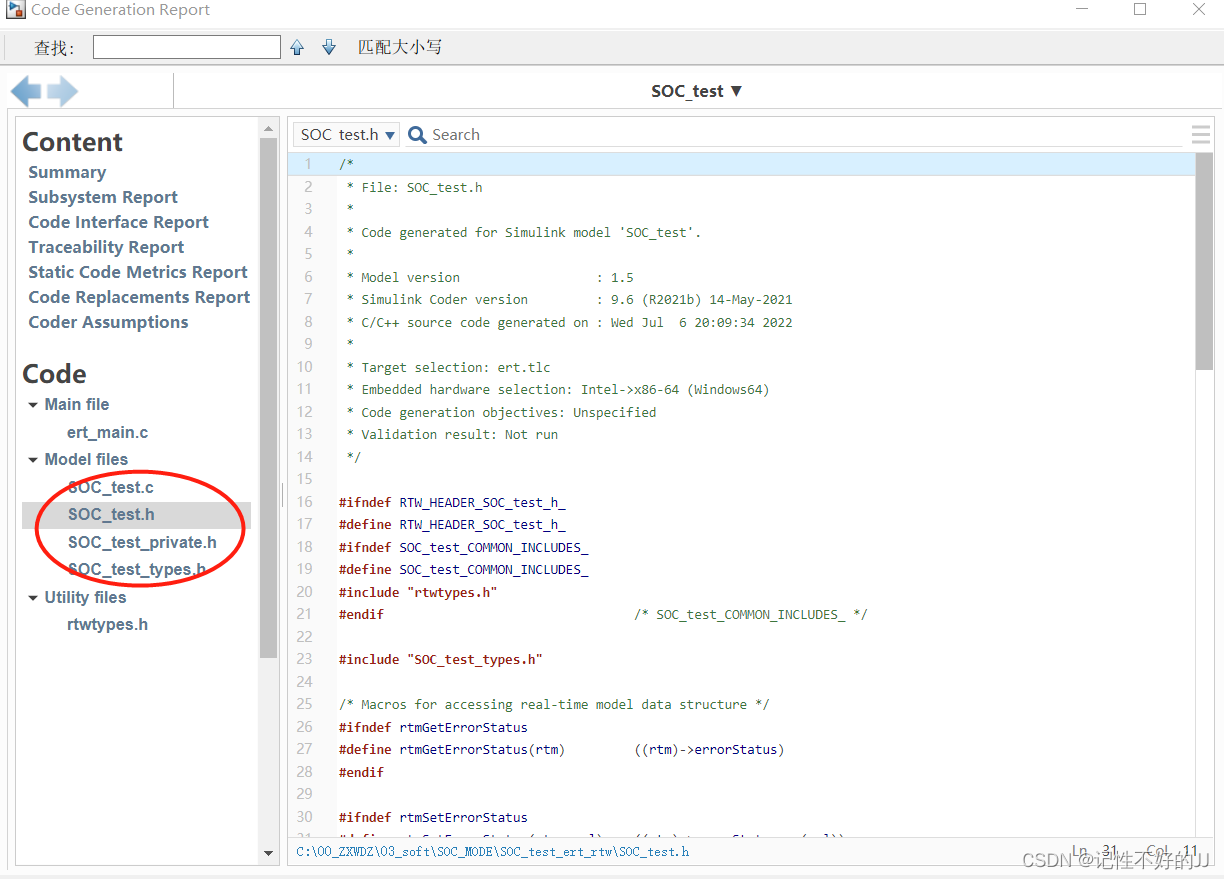
 将生成的文件拷贝进C工程里：

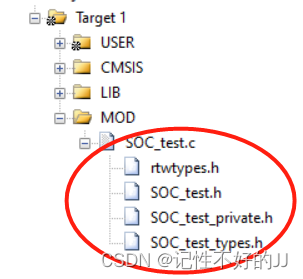
 找到里面的主功能函数，建模的时候采用原子子系统，生成代码的时候就有一个主功能函数，把它添加进500mS的调用程序中，再将模型的输入变量赋值，可以做个接口层，我这里直接赋一个测试值常量。

 方便起见，电流按1C设定，初始SOC=50%，这样如果放电状态下，15分钟的时间，SOC理论应该由50%下降至25%。

 

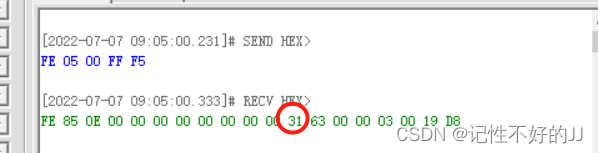
 初始计算出的SOC=0x31,即49%，实际上是49.9几。

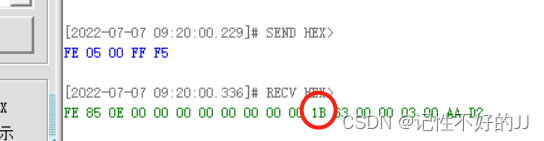
15分钟后，SOC=0x1B,即27%。基本功能实现。

 

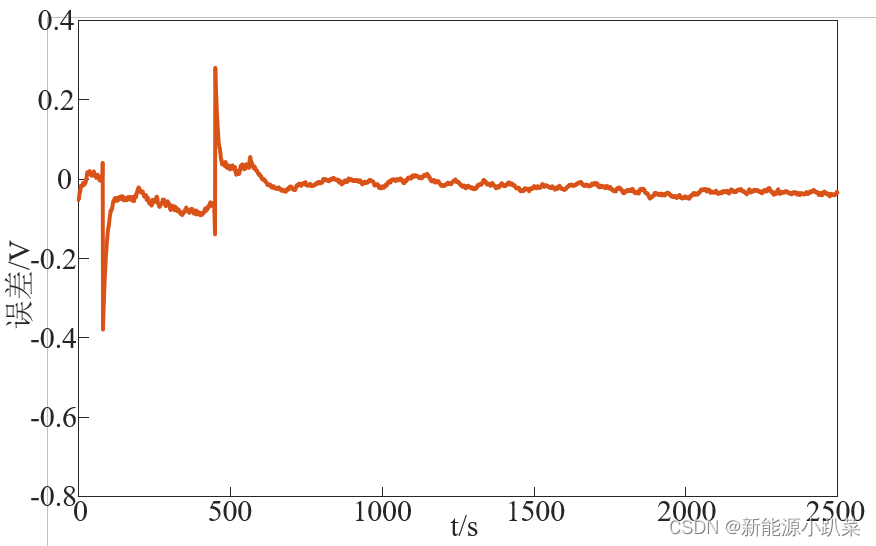
三、结果

       通过验证发现计算的误差还是比较大的，取决于MCU的算力，尤其是浮点运算这块，对于低串小容量设备来说，增加一些查表修正基本可以满足使用要求了。

     至此万里长征迈出了第一步，接下来还有9999步。~~！