原题链接：

PTA | 程序设计类实验辅助教学平台

题目描述：

下图转自“英式没品笑话百科”的新浪微博 —— 所以无论有没有遇到难题，其实都不用担心。

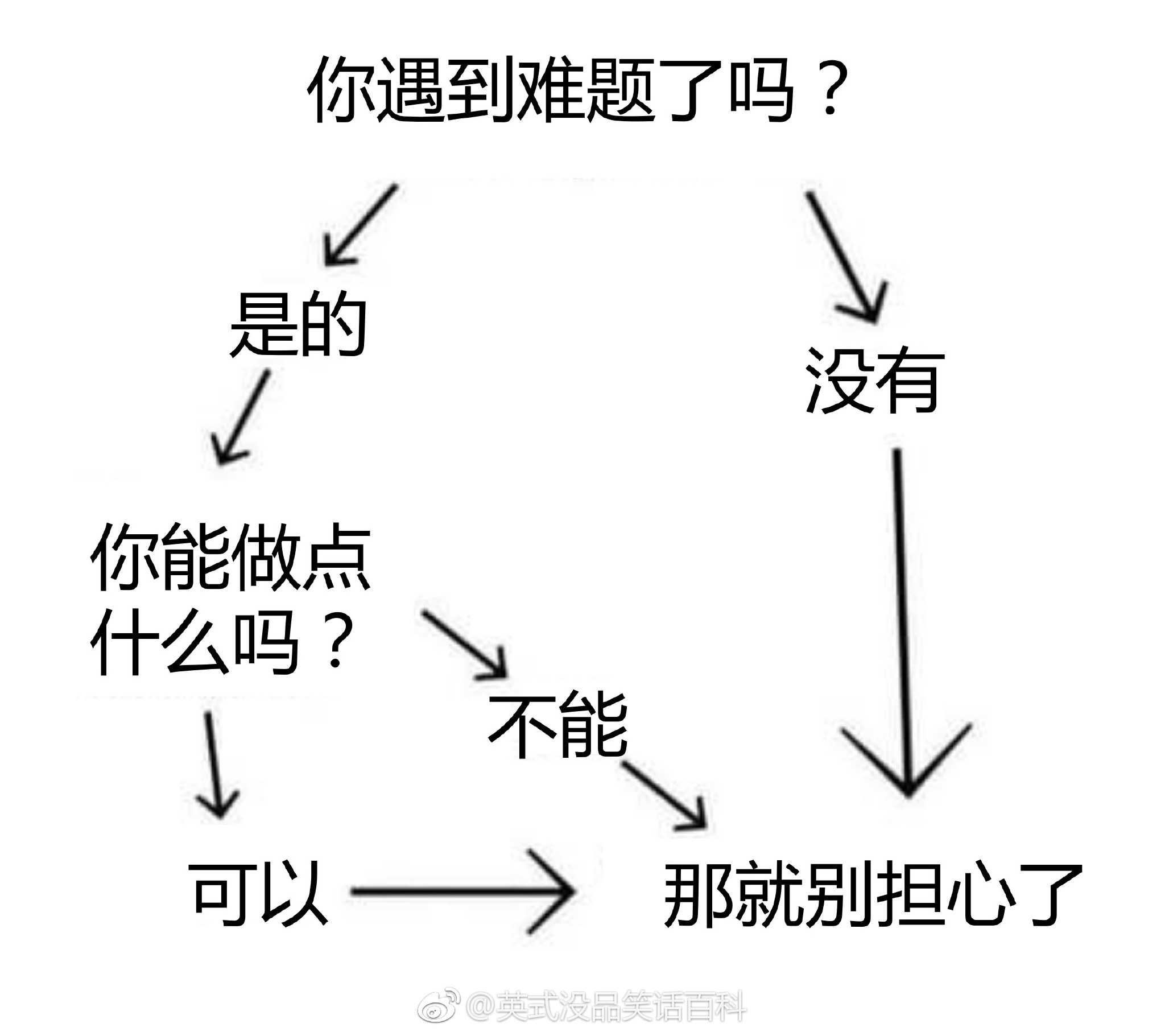
博主将这种逻辑推演称为“逻辑自洽”，即从某个命题出发的所有推理路径都会将结论引导到同一个最终命题（开玩笑的，千万别以为这是真正的逻辑自洽的定义……）。现给定一个更为复杂的逻辑推理图，本题就请你检查从一个给定命题到另一个命题的推理是否是“逻辑自洽”的，以及存在多少种不同的推理路径。例如上图，从“你遇到难题了吗？”到“那就别担心了”就是一种“逻辑自洽”的推理，一共有 3 条不同的推理路径。

输入格式：

输入首先在一行中给出两个正整数 N（1<N≤500）和 M，分别为命题个数和推理个数。这里我们假设命题从 1 到 N 编号。

接下来 M 行，每行给出一对命题之间的推理关系，即两个命题的编号 S1 S2，表示可以从 S1 推出 S2。题目保证任意两命题之间只存在最多一种推理关系，且任一命题不能循环自证（即从该命题出发推出该命题自己）。

最后一行给出待检验的两个命题的编号 A B。

输出格式：

在一行中首先输出从 A 到 B 有多少种不同的推理路径，然后输出 Yes 如果推理是“逻辑自洽”的，或 No 如果不是。

题目保证输出数据不超过 109。

输入样例 1：

输出样例 1：

3 Yes

输入样例 2：

输出样例 2：

3 No

解题思路：

注意：题目要求判断是否逻辑自洽是判断从A点起的所有路径是否都能够到达B。

记忆化搜索、树形dp。

设f[i]为顶点i到达顶点B的路径数，那么f[i]=i的所有子节点到达顶点B的路径总数。

重点来了，如何判断是否逻辑自洽？

其实可以在dfs的过程中同时判断，只要路径中有任何一个f[i]为0，也就是到达B的路径数为0，即不满足逻辑自洽，否则满足逻辑自洽。

代码（CPP）：

给出两份代码

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e3 + 10;
int n, m, A, B, cnt;
vector<int> G[maxn];
int Cnt[maxn];
bool flag = true;int dfs(int v)
{if(Cnt[v])  // 备忘录，，记忆化搜索，查备忘录内有无记录，有则不需要再次计算return Cnt[v];for (int i = 0; i < G[v].size(); i++){Cnt[v] += dfs(G[v][i]);}if(Cnt[v] == 0)  // 如果路径上有任何一个点无法到达B，则这个逻辑图不是逻辑融洽的flag = false;return Cnt[v];
}
int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin >> n >> m;while(m--){int u, v;cin >> u >> v;G[u].push_back(v);}cin >> A >> B;Cnt[B] = 1;dfs(A);cout << Cnt[A] << " " << (flag ? "Yes" : "No");return 0;
}

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e3 + 10;
int n, m, A, B, cnt;
vector<int> G[maxn];
int Cnt[maxn];
bool flag = true;int dfs(int v)
{if(Cnt[v])  // 备忘录，，记忆化搜索，查备忘录内有无记录，有则不需要再次计算return Cnt[v];for (int i = 0; i < G[v].size(); i++){Cnt[v] += dfs(G[v][i]);}if(Cnt[v] == 0)  // 如果路径上有任何一个点无法到达B，则这个逻辑图不是逻辑融洽的flag = false;return Cnt[v];
}
int main()
{
//     freopen("in.txt", "r", stdin);ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin >> n >> m;while(m--){int u, v;cin >> u >> v;G[u].push_back(v);}cin >> A >> B;Cnt[B] = 1;dfs(A);cout << Cnt[A] << " " << (flag ? "Yes" : "No");return 0;
}