目录

0. 写在前面

1. 舵轮是什么？

1.1 为什么取名叫舵轮？

1.2 AGV舵轮长啥样？

1.3. AGV舵轮如何交互？

2. 双舵轮的运动分解

2.1 问题描述

2.2 运动分解的公式推导

3. 双舵轮的运动合成

3.1 问题描述

3.2 运动合成的公式推导

4. 最后的话

---

0. 写在前面

无人车，要做到无人化，但本质上，它是个车。既然是车，就离不开各种轮子。

这次，我想和你聊一聊舵轮，进一步，聊一聊双舵轮的运动解算（也叫运动分解）与运动合成。

1. 舵轮是什么？

在正式讨论前，先简单介绍一下舵轮。

舵轮，其实是一种非常常见形式的运动轮。比如，我们耳熟能详的杂技车，本质上就是一个舵轮。我在网上搜索了“杂技车”（或者“单轮车”），找到了下面的图片（侵删）。

我相信，不管你骑没骑过，都不妨碍参照它来理解什么是舵轮。

我们用一些通俗易懂的话来总结，它的特点是结构简单，行走与转向功能在同一滚动轮上实现。你看，踏板围绕在滚动轮的轴心上下翻动，转动踏板可使轮子前后移动；骑车的人通过扭动身体改变滚动轮的朝向。

1.1 为什么取名叫舵轮？

至于为什么取名叫舵轮，刚接触这个专业名称的时候，我也有这个疑问，还特意去查了查。

一般来说，“舵”的解释是，船、飞机等控制方向的装置；而“舵轮”是轮船、汽车等的方向盘。另有一种说法，位于船舶驾驶室中，用于控制船舵运动、改变船舶航向的手轮，称为舵轮。

我兜兜转转查了一圈，大概意思总结一下，舵轮是用来改变方向的。有一句话叫做，掌握了舵轮就掌握了前进的方向。

对于今天讨论的舵轮，我推测，取这个名字，可能就是因为轮子的方向可以改变。也就是滚动轮的方向（又称舵向角）相对于车体是可变的。

其实，还有个特点，如果你仔细观察，会发现，改变舵轮的中心轴朝向时，舵轮和地面的接触点可以保持不变，就好像轮子上方有个转盘可以扭动车轮的朝向一样。

其实，在AGV行业里，舵轮就是这么设计的。

1.2  AGV舵轮长啥样？

简单说，AGV舵轮代表性形式有下面两种。左图是卧式，便于做低整车高度，右图是立式，能做小车子的长宽尺寸。值得注意的是，图中红色箭头所指的位置，就是所谓的“舵”——起到改变滚动轮方向的齿轮。

如果你仔细观察一下，两种形式只是改变了行走和转向电机的摆放位置而已。

我们用稍微专业点的话来总结一下，舵轮是集成了行走电机、转向电机、减速机等组件的机械结构，集行走、牵引和转向功能为一体，可以荷载和牵引较重货物。

其中，行走电机和转向电机是舵轮的执行机构，分别由行走电机驱动器和转向电机驱动器直接控制。有时，两个电机驱动器会封装在一个外壳里，或做到一张嵌入式控制板上。这种外形的改变不影响我们对舵轮控制形式的理解。

1.3. AGV舵轮如何交互？

在工业AGV上，通常来说，舵轮电机驱动器使用伺服电机，以低压永磁无刷伺服电机为主，因此，可交互的信息很多，比如电机转速、电机扭矩、电机的绝对位置、电机加速度、电机电压电流等。

但在一些大功率场合，也会使用变频电机和外装轮速计或角度编码器来组合使用。

为了便于后续对舵轮车进行运动分解，我们将这些信息进行提炼，并对模型进行抽象：

1） 舵轮转向电机的转角可控，状态为舵轮的舵向角大小，简称舵向角，记作θ；

2） 舵轮行走电机的转速可控，状态为舵轮接地点的线速度大小，简称线速度，记作vt；

3） 舵轮的线速度方向恒等于舵向角；

关于舵轮的舵向角θ的测量，比较简单，一般直接使用伺服电机内置的绝对值编码器的实时数据。

关于舵轮的线速度vt，需要由电机实时转速（rpm）换算而来。一般而言，为了增大滚动轮的输入扭矩，行走电机不直接输出扭矩，而是先经过减速机，再传递给滚动轮。在不考虑轮子在地面上可能存在的滑动时，舵轮车线速度vt的公式为：

其中，

n为电机转速，单位为rpm（每分钟的转动圈数）；

i为减速机的减速比，无量纲；

d为滚动轮的外径，单位为米；

vt为舵轮转动轴的线速度，单位为m/s（米/秒）；

我们都知道，对于物体的运动状态，通常会抽象成线速度和角速度。其中，线速度是矢量，带有方向，因此，可由上一节获得的线速度值vt和舵向角θ共同来表达。而角速度w是一个标量，可通过公式

进行计算。其中，r为舵轮接地点到转向中心点（整车的转向中心点，也叫瞬心）的距离。这样一来，舵轮的参数也可由线速度大小、角速度大小、舵向值（vt，w，θ）三个参数来表达。

需要注意的时，到目前为止，我们讨论的对象依旧是单个舵轮。

2. 双舵轮的运动分解

2.1 问题描述

为了讨论方便，在不失一般性的前提下，我们选择前后对称排布的双舵轮车进行讨论。

理由有两点：

1.  双舵轮的结构形式，可实现车辆的全向移动，是一种形式简洁的全向车。

2. 对于双舵轮的研究结果，只需要增加有限的约束，便可快速应用到单舵轮的场合。比如，假定后轮的舵向角恒定不变，速度与整车质心运动速度动态匹配，也就是说把后轮变成定角度的随动轮，那么，模型便可对应到单舵轮。

 

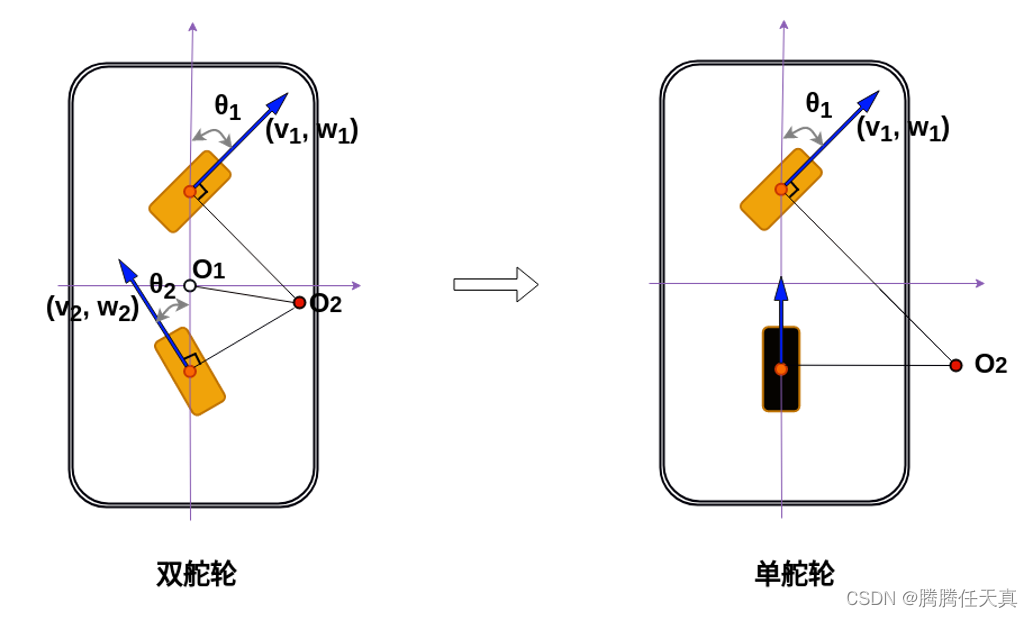
因此，我们讨论的问题就变成了双舵轮的运动控制了。

当我们控制双舵轮AGV去跟随路径时，导航算法会给AGV下发目标线速度大小vt、目标线速度方向θ和目标角速度w。这里需要区分两个概念，舵轮自身的航向角和AGV车体运动中心（一般为车体几何中心，但也可以自由设定。本文假定AGV运动中心为车体的几何中心）的航向角，两者不一定相等，准确的说，在导航的动态过程中，大部分时间是不相等的。

基于以上概念，我们建立车体坐标系，采用东北天（ENU）形式，车体逆时针旋转时为正，顺时针旋转时为负。我们在后续讨论中，舵轮的航向角的零位定义在车体的正北向，也就是当车体向前时，前后舵轮的舵向角为0。结合正负角度的定义有，舵轮逆时针旋转时角度增加，顺时针旋转时角度变小，取值范围为[-180°，180°]。

现在，来一句话描述问题。

假设AGV的运动中心在两个舵轮连线的中点，当导航算法给AGV下发控制指令，含有目标线速度大小、目标线速度方向和目标角速度，记作（vt，w，θ），我们通过运动分解，得到两个舵轮各自的线速度和舵向角，记作（v1，θ1）和（v2，θ2）。

2.2 运动分解的公式推导

为简化讨论的过程，我们可以将双舵轮AGV的模型进一步简化，认为两个舵轮旋转中心支点刚性连接，然后，以两个舵轮旋转中心连线的中点，来讨论AGV的线速度和角速度。

已知下发给双舵轮AGV运动中心的参数为（v，w，θ），两舵轮之间的距离为d，其中，两个舵轮的运动状态分别表示为（v1，w1，θ1）和（v2，w2，θ2）。

由于整个AGV车体假设为刚性连接，因此两个舵轮、车体运动中心以及车体任意一点的旋转角速度w是相同的。我们的目标是，通过运动分解，获得两个舵轮的目标控制值，且只需要包含线速度和舵向角，即（v1，θ1）和（v2，θ2）。

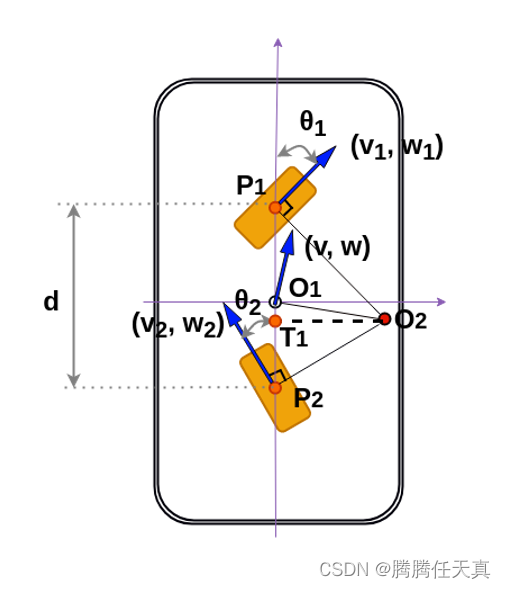
下面，我们一步步进行推导。

1）计算AGV转向中心的转动半径O1O2；

2）计算前后舵轮各自的转动半径：(从O2点向线段P1P2做辅助垂线O2T1）

3) 计算前后舵轮的舵向角：

4）计算前后舵轮的线速度：

 总得来说，整个推导过程还是相对比较简单的。

特别地，当θ1或θ2强制为0时，即为单舵轮结构。此时，一般而言，整车的移动中心将移动到对应的舵轮旋转中心。调整之后，依旧可以用上述四步的方法，进行类似地推导。

3. 双舵轮的运动合成

3.1 问题描述

在有些情况，AGV控制系统需要获得整体的运动状态，供其他系统进行数据融合。比如，SLAM系统可使用车辆的里程计信息，增加定位数据的稳定性，提高定位的精度等。又比如，在导航系统中，轨迹规划控制器需要实时获取车辆的线速度和角速度，以便形成控制闭环。

这时，就需要用到双舵轮的运动合成。

在正式合成之前，我们先定义一下待解决的具体问题。

假设AGV的运动中心在两个舵轮连线的中点，当我们已知两个舵轮各自的线速度和舵向角，记作（v1，θ1）和（v2，θ2），计算整个AGV中心点的状态信息，含有线速度大小、角速度和线速度方向，记作（v，w，θ）。

3.2 运动合成的公式推导

已知：两个舵轮各自的线速度和舵向角，分别为（v1，θ1）和（v2，θ2）；

求：AGV中心点的目标线速度大小、目标角速度和目标线速度方向，记作（v，w，θ）。

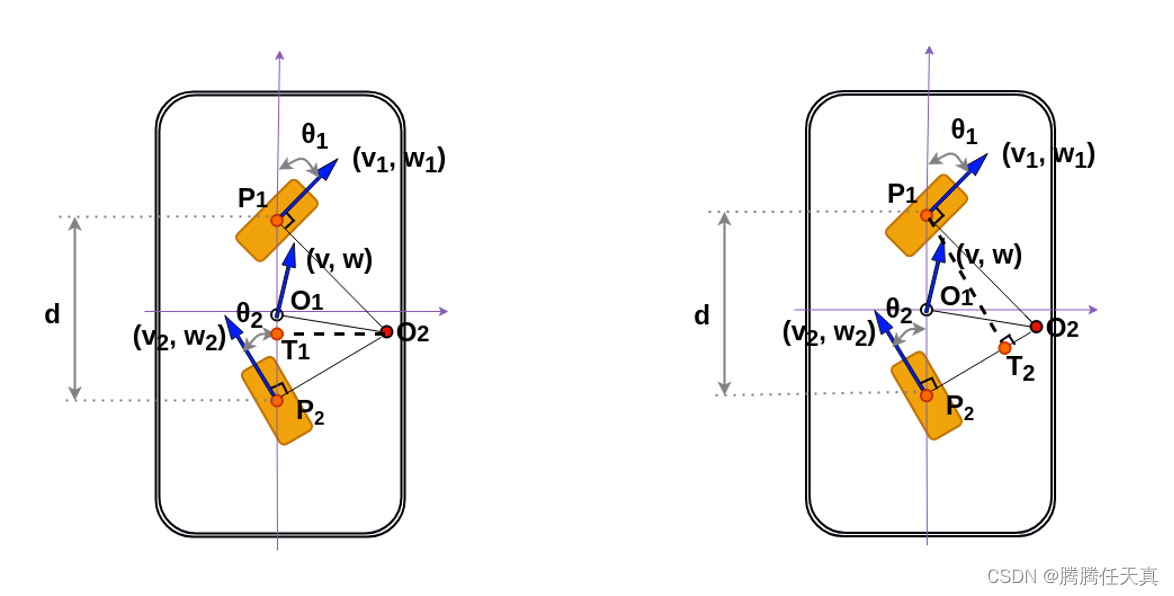
因此，运动合成的推导过程如下：

1）计算前后舵轮的转向半径r1和r2：

如右图所示，为了便于计算舵轮运动半径r1（即O2P1)，增加了辅助垂线P1T2；

r2（即O2P2）的求法类似，不赘述，直接展示公式。

2）计算前后舵轮的角速度；

或有

 

3）通过前舵轮或后舵轮，计算AGV中心点的航向角。（使用左图推导）

或有

4）通过前舵轮或后舵轮，计算AGV中心点的转向半径。

或有

5）计算AGV中心点的线速度大小；

4. 最后的话

双舵轮的结构形式简单，运动分解和合成的过程也很直观。

公式无需记忆，使用的时候，临时推导即可快速获得。

当假定其中一个舵轮的舵向角恒定不变，速度与整车运动中心运动速度动态匹配，也就是说把该轮变成定角度的随动轮，那么，本文的方法就可以应用到单舵轮的场合。

对于两个以上舵轮构成的AGV车辆，套用本文的思路和步骤，也能顺利地解决问题。

好了，今天就到这里，希望对你有帮助。