目录
摘要:
主要内容:
程序思路:
储能选址定容优化模型:
(1)节点电压波动:
(2)负荷波动:
(3)储能系统容量:
改进的多目标粒子群算法:
(1)自适应权重:
(2)交叉变异:
(3)种群全局最优解的选取:
算例分析及结果:
本文Matlab代码分享:
摘要:
以系统节点电压水平(电网脆弱性)、网络损耗以及储能系统总容量为目标建立了储能选址定容优化模型。求解过程中提出了一种改进多目标粒子群算法(improved multi—objective particle swarm optimizer,IMOPSO)。该算法根据粒子与种群最优粒子的距离来指导惯性权重的取值,使得各粒子的惯性权重可以自适应调整,并在二者距离较小时引入交叉变异操作,避免陷入局部最优解,同时采用动态密集距离排序来更新非劣解集并指导种群全局最优解的选取,在保持解集规模的同时使解的分布更均匀。为避免决策者偏好对最终结果的影响,采用基于信息熵的序数偏好法从最优Pareto解集中选取储能的最优接入方案。以IEEE33节点配电系统为例进行仿真验证,结果表明该方法在储能选址定容问题求解中具有很好的收敛性以及全局搜索能力。
主要内容:
分布式电源的出力具有不确定性,易受环境因素的影响,因此其大量接入将对配电网的安全稳定运行带来很大影响。储能系统具有快速能量响应能力,能够在一定程度上平抑分布式电源带来的不利影响。储能系统接入位置与其容量的不同对其平抑效果的影响很大,因此其接入位置的选择与容量的确定是亟需解决的一个问题。
本文首先建立储能系统选址定容多目标优化模型,其次就多目标粒子群算法(multi.objectiveparticle swarm optimizer,MOPSO)在求解过程中存在的一些问题进行改进,提出一种改进的多目标粒子群算法(improved multi—objective particle swarrfloptimizer,IMOPSO),并以基于信息熵的序数偏好法(technique for order performance by similarity toideal solution,TOPSIS)求解储能的最优接入方案,最后以IEEE一33节点配网系统为例进行仿真分析,验证所提方法的有效性。
程序思路:
储能选址定容在智能算法中的实现过程不难,刚开始变量定义部分,主要是涉及储能选址的位置、容量和储能出力,以这两部分变量作为优化变量,通过设置最大值和最小值确定变量上下限范围。
下一步的关键点就是约束处理部分,对于储能soc约束,在单目标实现过程中可以采用罚函数的表达方式,但是在多目标求解过程中最好是采用绝对约束表达方式,因为多目标的帕累托解集有可能将不满足约束条件的目标值也筛选进入解集中,就会导致解集的不准确。最后就是设置目标值,对于配电网节点系统,要注意潮流计算方式的选择和储能出力对系统影响,然后设置不同的目标值。上述都设置清楚后,采用智能算法进行求解就简单了,多目标算法要注意采用拥挤距离识别方法保证解集分布的合理性。
本程序注释详细,适合初学者模仿学习。
储能选址定容优化模型:
配电网储能选址定容受诸多因素的影响,是一个多目标优化问题。分布式电源大量接入配电网后,将使其电能质量恶化,其中电压波动问题愈加突出,并加剧系统负荷波动,而储能系统能够在一定程度上改善这些不利影响。同时由于储能系统的成本相对较高,在配置时其容量也是一个不得不考虑的问题。因此,本文综合考虑储能系统带来的效益以及储能系统的成本,选取以下3个指标作为目标函数。
(1)节点电压波动:
节点电压是表征系统稳定性以及电能质量的重要指标之一。系统中各节点电压均应保持在一定水平,同时其波动也应维持在较小水平。接入分布式电源后,节点电压水平有了一定程度的提升,但其波动却加剧。因此,选取节点电压波动的总和作为储能系统选址定容的目标函数,其数学计算式为:

(2)负荷波动:
配电网中接入分布式电源后,由于其出力的不确定性将使系统负荷波动加剧,对发电企业以及用户造成不利影响。储能系统具有快速能量吞吐能力,能够对系统负荷波动进行平抑。负荷波动的计算公式如式(2)所示:
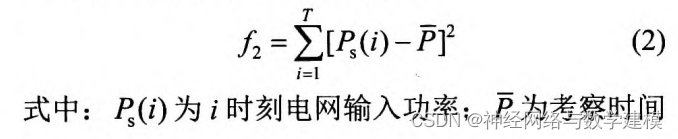
(3)储能系统容量:
在考虑储能系统效益的同时也应考虑其成本,选取储能系统的总容量作为目标函数。以考察时间内储能系统的最大充/放电能量作为其额定容量。

改进的多目标粒子群算法:
本文从下面三个方面对粒子群算法进行改进。
(1)自适应权重:
在PSO算法中,惯性权重W的取值对其收敛性能有重要影响。常用的W取值方法大多是随着迭代次数的递增而线性或非线性的递减,这种方法没有考虑迭代过程中粒子的特性,W的取值缺乏指导。粒子位置向量与种群全局最优解的差值可以体现粒子与种群最优粒子的差距程度。当其值较大时表示当前粒子与种群最优粒子差距较大,此时W的取值也应较大,使得该粒子具有较好的全局搜索能力;而当其值较小时则表示其与种群最优粒子差距较小,此时应使其具有较好的局部搜索能力,W的取值也应较小。本文以粒子与种群最优粒子的差距程度作为指导来进行W的取值,随着差距程度的不同非线性地调整W的大小。
(2)交叉变异:
PSO算法在迭代寻优时存在早熟收敛问题,容易陷入局部解。本文将遗传算法中的交叉变异操作引入粒子群算法中,对粒子的位置向量进行交叉变异,用以提高种群的多样性。以粒子位置向量与种群全局最优解的差值X作为交叉变异的依据,具体步骤为:

(3)种群全局最优解的选取:
粒子群算法在进行种群更新时,需要跟踪粒子的历史最优解和种群全局最优解。单目标粒子群算法中,种群全局最优解可以通过比较粒子适应度函数的大小直接得到,而在多目标粒子群算法中,其每次迭代结果均为一组互不支配的Pareto解。因此,如何从Pareto解集中选取种群全局最优解也是一个需要考虑的问题。为保证Pareto解集中解的多样性和均匀性,在密集距离排序的基础上,从密集距离较大的前20%个Pareto解中随机选出种群全局最优解,用于指导种群的更新。
算例分析及结果:
本文采用IEEE一33节点配电网系统来进行仿真分析,其结构如图所示。网络总负荷为3 715 kw+i2300 kvar,典型日曲线如图下所示。系统额定电压为12.66 kV,节点电压允许范围为0.9~1.05 pu。
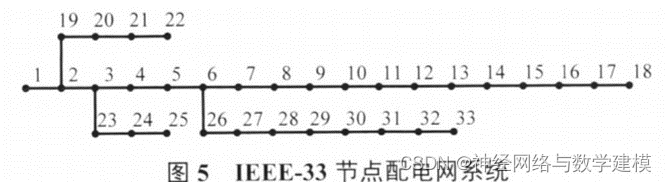
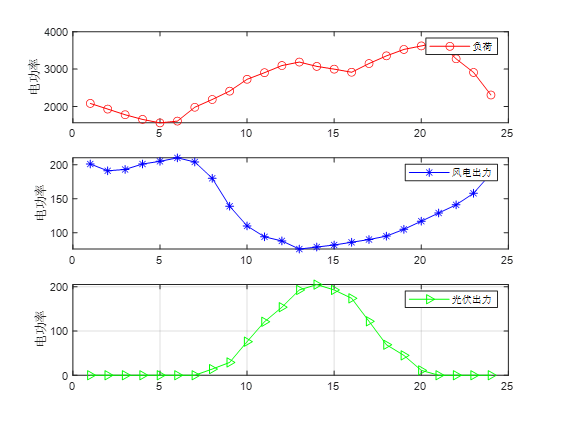
通过运行本文代码分别得到Pareto最优图像和两种储能的详细配置情况。

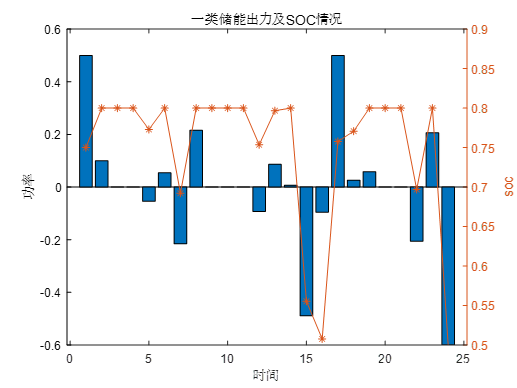
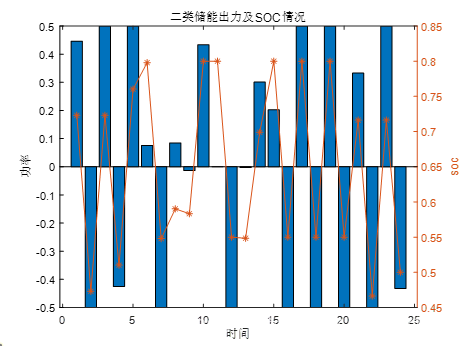
本文Matlab代码分享:
![]()