红黑树的改装

🚀由于前面的博客中分享过红黑树的插入和删除: 链接，所以本文中使用的就是那篇文章中的红黑树。就是用这颗红黑树同时封装出map和set。在本文中就将删除的代码去掉了（太长了），在后面封装的时候也就不涉及map和set的erase功能的实现（就是对红黑树erase的改造，并且改造过程与insert类似）。

红黑树源码：

#pragma once
#include <time.h>
#include <stdlib.h>
namespace gy_rbtree
{typedef enum color{BLACK,RED}color;template<class K, class V>struct TreeNode{public:TreeNode<K, V>(const pair<K, V>& kv):_kv(kv), _col(RED){}public:color _col;pair<K, V> _kv;TreeNode<K, V>* _left = nullptr;TreeNode<K, V>* _right = nullptr;TreeNode<K, V>* _parent = nullptr;};template<class K, class V>class rbtree{public:typedef TreeNode<K, V> node;public:rbtree() = default; //默认构造~rbtree() { Destroy(_root); _root = nullptr; } //析构rbtree(const rbtree& t) { _root = Copy(t._root); } //拷贝构造bool insert(const pair<K, V>& kv){//根节点为空if (_root == nullptr){_root = new node(kv);_root->_col = BLACK;return true;}node* cur = _root;node* parent = nullptr;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else{//已经存在了return false;}}//找到了属于它的位置,插入cur = new node(kv);cur->_parent = parent;if (kv.first < parent->_kv.first){parent->_left = cur;}else{parent->_right = cur;}//只要parent结点存在，并且其结点为颜色为红色就需要调整while (parent && parent->_col == RED){node* grandfather = parent->_parent;if (parent == grandfather->_left){//1,第一种情况，存在叔叔结点，并且为红色if (grandfather->_right && grandfather->_right->_col == RED){//祖父结点变红，父亲结点和叔叔结点变黑，继续向上调整，直到根节点为止。grandfather->_col = RED;parent->_col = BLACK;grandfather->_right->_col = BLACK;cur = grandfather;parent = cur->_parent;}//2,叔叔结点不存在或者为黑色else{//2.1 cur为parent的左子树，那么只需要祖父为根的树右旋即可if (cur == parent->_left){grandfather->_col = RED;parent->_col = BLACK;RotateR(grandfather);}//2.2 cur为parent的右子树，那么先对parent左旋，在对祖父右旋else if (cur == parent->_right){grandfather->_col = RED;cur->_col = BLACK;RotateLR(grandfather);}break;}}else{if (grandfather->_left && grandfather->_left->_col == RED){grandfather->_col = RED;parent->_col = BLACK;grandfather->_left->_col = BLACK;cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_right){grandfather->_col = RED;parent->_col = BLACK;RotateL(grandfather);}else if (cur == parent->_left){grandfather->_col = RED;cur->_col = BLACK;RotateRL(grandfather);}break;}}}_root->_col = BLACK;return true;}private:void RotateL(node* parent){node* subR = parent->_right;node* subRL = subR->_left;parent->_right = subRL;if (subRL){subRL->_parent = parent;}subR->_left = parent;node* ppnode = parent->_parent;parent->_parent = subR;if (ppnode == nullptr){_root = subR;subR->_parent = nullptr;}else if (ppnode->_left == parent){ppnode->_left = subR;subR->_parent = ppnode;}else{ppnode->_right = subR;subR->_parent = ppnode;}}void RotateR(node* parent){node* subL = parent->_left;node* subLR = subL->_right;parent->_left = subLR;if (subLR){subLR->_parent = parent;}subL->_right = parent;node* ppnode = parent->_parent;parent->_parent = subL;if (ppnode == nullptr){_root = subL;subL->_parent = nullptr;}else if (ppnode->_left == parent){ppnode->_left = subL;subL->_parent = ppnode;}else{ppnode->_right = subL;subL->_parent = ppnode;}}void RotateLR(node* parent){node* subL = parent->_left;RotateL(subL);RotateR(parent);}void RotateRL(node* parent){node* subR = parent->_right;RotateR(subR);RotateL(parent);}void Destroy(node* root){if (root == nullptr) return;Destroy(root->_left);Destroy(root->_right);delete root;}node* Copy(node* root){if (root == nullptr) return;node* newroot = new node(root->_kv);newroot->_left = Copy(root->_left);newroot->_right = Copy(root->_right);return newroot;}private:node* _root = nullptr;};}

源码中的实现一颗红黑树封装出map和set

🚀很多小伙伴可能会有疑惑？set对应的红黑树结点中存储的是KEY，而map对应的红黑树结点中存储的是KEY-VALUE，而要将红黑树封装成map和set显然要两棵红黑树。下面看下源码中是如何完成的：

截取了源码中的一部分：


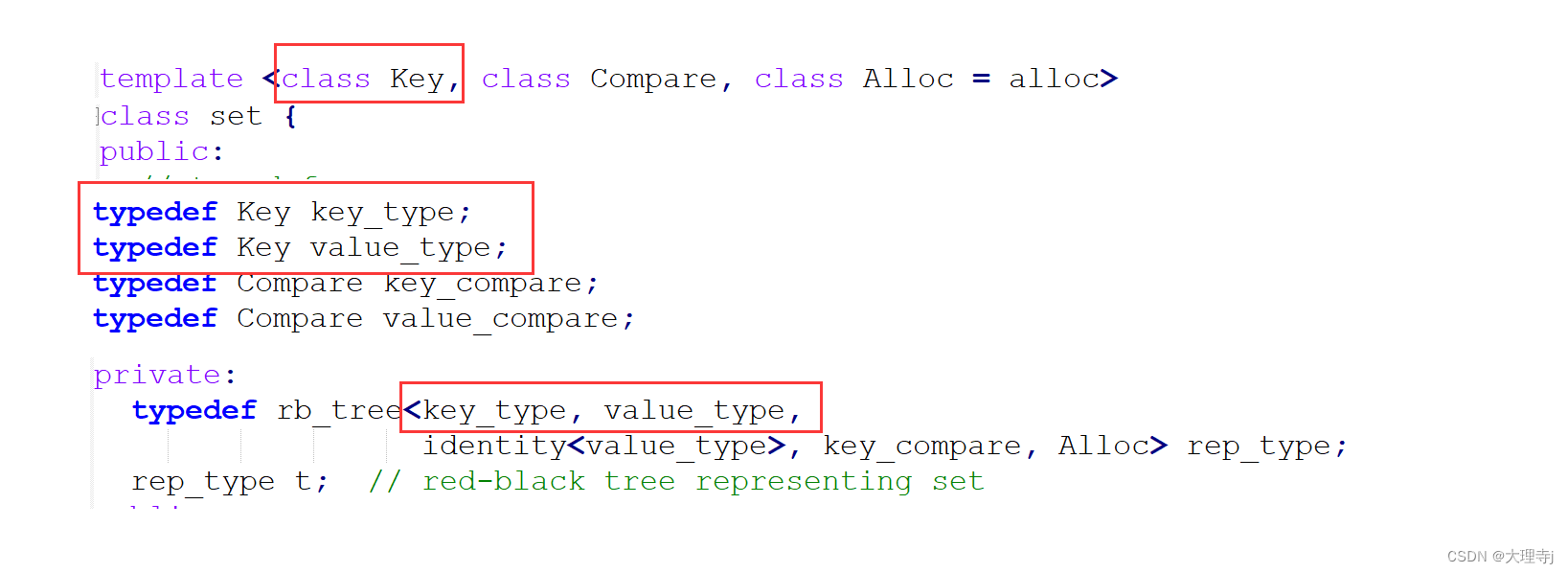
🚀源码中map传给红黑树的模板参数为K和pair，set传给红黑树的模板参数为K和K，所以使用一个模板参数就可以让一颗红黑树封装出map和set（起始模板实例化后仍然会实例化出两个类，但是利用泛型提高的代码的复用度）。
🚀还有让人疑惑的一点就是map和set同时向红黑树传了K这个模板参数，对于map来说是为了后面Find和Erase（插入和删除都需要key值），对于set来说完全是没有必要的只是为了配合map。

对红黑树的第一步改造

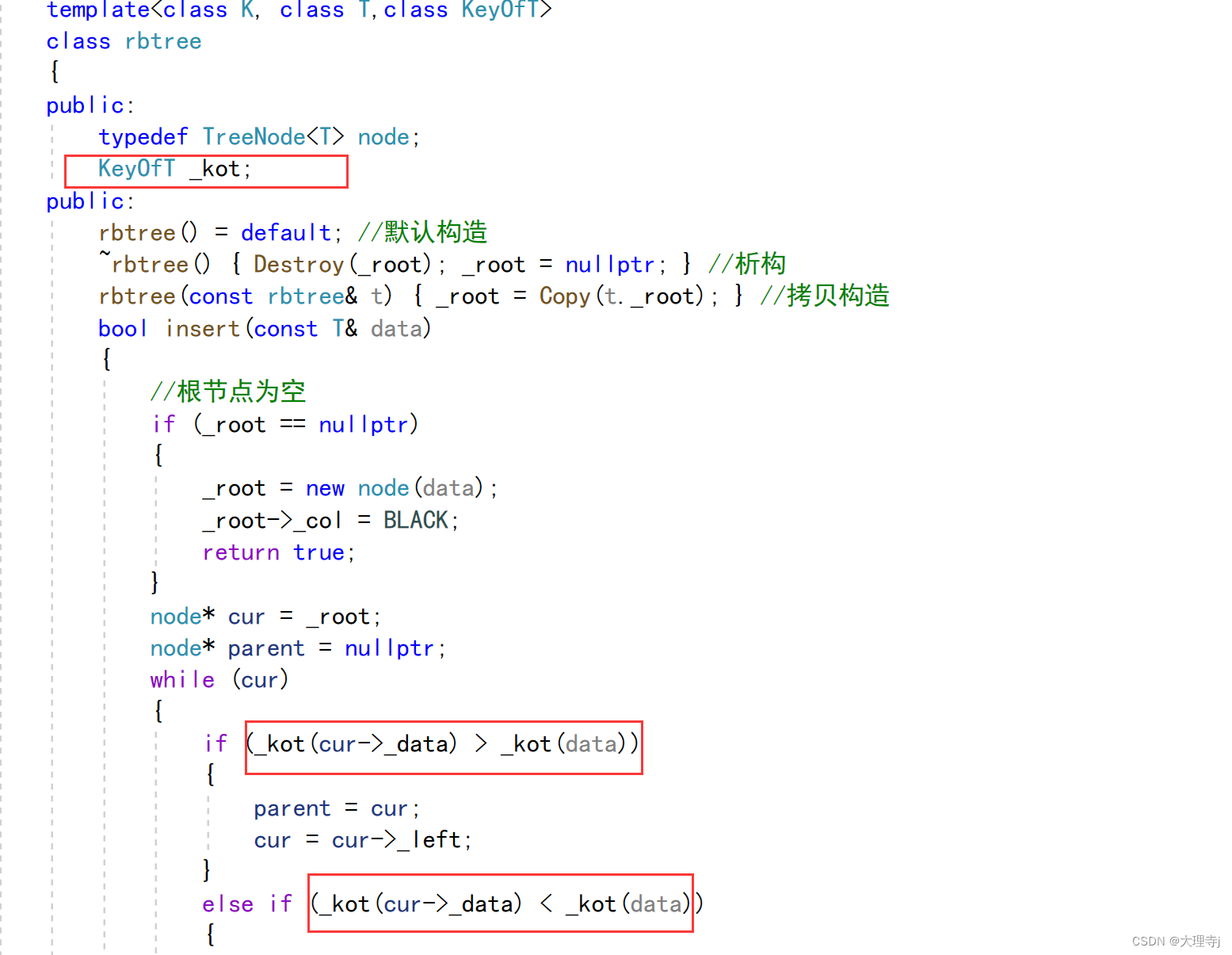
🚀对于红黑树的结点中存储的不再是一个pair，而是T类型的data，以便map传入的是pair，T就会实例化为pair，对于set而言传入的是key，T就实例化为key。

🚀同时还会面临一个问题就是，在插入，删除，查找的时候，都会面临要将目标内容与结点中的内容做比较，由于此时的红黑树中存储的是pair还是某个key值是不清楚的，所以比较的时候也无法比较，但无论是pair还是key我们在比较的时候都是用的key值（pair中的first值）来进行比较的。虽然红黑树不知道它存储的是pair还是单个的key，但是map和set是清楚的，所以map和set可以传给红黑树一个仿函数帮助红黑树来获取类型T中的key值。

对红黑树的第二步改造

map初步结构

template<typename K, typename V>
class map
{
private:struct Map_KeyOfT{const K& operator()(const pair<const K, V>& kv){return kv.fitst;}};
private:using tree = gy_rbtree::rbtree<K, pair<const K, V>, Map_KeyOfT>;tree _t;
};

set的初步结构

template<typename K>
class set
{
private:struct Set_KeyOfT{const K& operator()(const K& key){return key;}};
private:using tree = gy_rbtree::rbtree<K,K, Set_KeyOfT>;tree _t;
};

红黑树的进一步改造

迭代器的实现

🚀上面已经完成了map，set，红黑树的大体框架，下面进行一些缝缝补补即可。STL中的容器都会有它的迭代器，所以下面来实现一下红黑树的迭代器。

//正向迭代器
template<typename T,typename Ref,typename Ptr>
struct __rb_tree_iterator
{using Node = TreeNode<T>;using self = __rb_tree_iterator<T, Ref, Ptr>;Node* _node;bool operator==(const self& it) { return _node == it._node; }bool operator!=(const self& it) { return _node != it._node; }Ref operator*() { return _node->_data; }Ptr operator->() { return &operator*(); }self& operator++(){}self& operator--(){}self operator++(int){}self operator--(int){}
};

🚀主要就是完成++，–的逻辑，对于红黑树来说++之后的迭代器指向的应该是当前结点中序遍历的下一个结点。–之后迭代器指向的应该是当前结点中序遍历的前一个结点。

迭代器++的实现

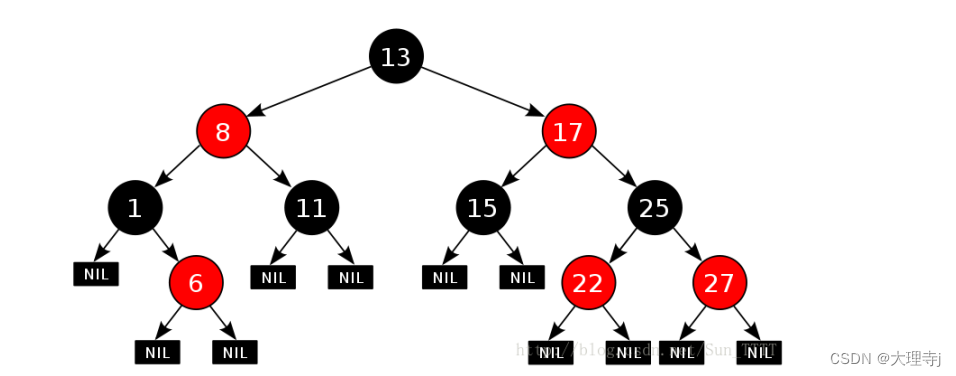
🚀找到中序遍历的下一个结点主要有两种情况
1，当前结点有右子树 -> 右子树的最左结点
例如，图中的17结点，它的下一个结点就是其右子树的最左节点22。
2，当前结点无右子树 -> 沿着此节点到根节点的路径上找到某节点的孩子节点不是其右子树的结点
例如，途中的6结点，它的下一个结点就是8结点，因为8号结点是第一个从6号结点到根的路径上的当前结点的子树不是其右子树的结点。

self& operator++()
{Node* cur = _node;if (cur && cur->_right) // 右子树存在{cur = cur->_right;while (cur->_left) cur = cur->_left;_node = cur;}else if(cur) //右子树不存在{Node* parent = cur->_parent;while (parent && parent->_right == cur){parent = parent->_parent;cur = cur->_parent;}_node = parent;}return *this;
}

迭代器–的实现

🚀与++的思路恰好相反，找到中序遍历的前一个结点的情况有两种：
1，当前结点有左子树 -> 左子树的最右结点
2，当前结点无左子树 -> 找到当前结点到根的路径上的某节点的孩子节点不是其左子树的结点。

self& operator--()
{Node* cur = _node;if (cur && cur->_left) //存在左结点{cur = cur->_left;while (cur->_right) cur = cur->_right;_node = cur;}else if (cur) //不存在左结点{Node* parent = cur->_parent;while (parent && parent->_left == cur){parent = parent->_parent;cur = cur->_parent;}_node = parent;}return *this;
}

库中红黑树模型

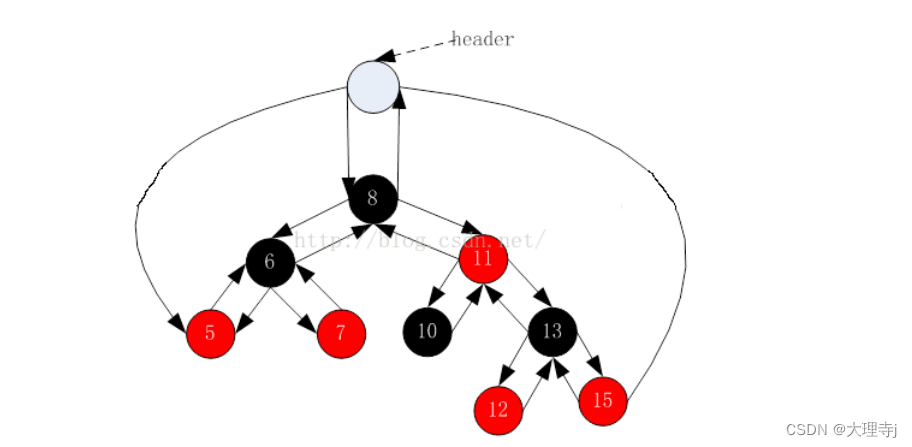
🚀在源码中多维护了一个header结点，其左子树指向最左结点，其parent结点指向根节点，最右结点的右子树指向header，根节点的parent结点指向header。

🚀库中最左结点的前一个结点和最右结点的下一个结点都是header，而本文中写的这种红黑树结构，最左结点的前一个是nullptr，最右结点的下一个是nullptr。

🚀begin和end的实现

iterator begin()
{node* cur = _root;if (_root == nullptr) return iterator(nullptr);while (cur->_left) cur = cur->_left;return iterator(cur);
}
iterator cbegin() 
{node* cur = _root;if (_root == nullptr) return const_iterator(nullptr);while (cur->_left) cur = cur->_left;return const_iterator(cur);
}
const_iterator end() { return iterator(nullptr); }
const_iterator cend() { return const_iterator(nullptr); }

对insert的改造

🚀库中insert函数返回值是一个pair，其中pair的first一个迭代器（如果插入成功则表示新插入位置的迭代器，如果失败则是冲突位置的迭代器），pair的second是bool类型表示是否插入成功。

🚀insert这样设计，主要是为了重载[ ]方便，[key]的作用是插入成功返回key对应的value，不成功返回已经存在的key对应的value。就是下面截图的意思。

pair<iterator,bool> insert(const T& data)
{//根节点为空if (_root == nullptr){_root = new node(data);_root->_col = BLACK;return make_pair(iterator(_root),true);}node* cur = _root;node* parent = nullptr;while (cur){if (_kot(cur->_data) > _kot(data)){parent = cur;cur = cur->_left;}else if (_kot(cur->_data) < _kot(data)){parent = cur;cur = cur->_right;}else{//已经存在了return make_pair(iterator(cur),false);}}//找到了属于它的位置,插入cur = new node(data);node* ret = cur;cur->_parent = parent;if (_kot(data) < _kot(parent->_data)){parent->_left = cur;}else{parent->_right = cur;}//只要parent结点存在，并且其结点为颜色为红色就需要调整while (parent && parent->_col == RED){node* grandfather = parent->_parent;if (parent == grandfather->_left){//1,第一种情况，存在叔叔结点，并且为红色if (grandfather->_right && grandfather->_right->_col == RED){//祖父结点变红，父亲结点和叔叔结点变黑，继续向上调整，直到根节点为止。grandfather->_col = RED;parent->_col = BLACK;grandfather->_right->_col = BLACK;cur = grandfather;parent = cur->_parent;}//2,叔叔结点不存在或者为黑色else{//2.1 cur为parent的左子树，那么只需要祖父为根的树右旋即可if (cur == parent->_left){grandfather->_col = RED;parent->_col = BLACK;RotateR(grandfather);}//2.2 cur为parent的右子树，那么先对parent左旋，在对祖父右旋else if (cur == parent->_right){grandfather->_col = RED;cur->_col = BLACK;RotateLR(grandfather);}break;}}else{if (grandfather->_left && grandfather->_left->_col == RED){grandfather->_col = RED;parent->_col = BLACK;grandfather->_left->_col = BLACK;cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_right){grandfather->_col = RED;parent->_col = BLACK;RotateL(grandfather);}else if (cur == parent->_left){grandfather->_col = RED;cur->_col = BLACK;RotateRL(grandfather);}break;}}}_root->_col = BLACK;return make_pair(iterator(ret),true);
}

map中[ ]的重载

V& operator[](const K& key)
{pair<iterator, bool> res = insert(make_pair(key, V()));return ( * (res.first)).second;
}

🚀res.first表示结点的迭代器，对其解引用就是对应的结点，结点的second就是key对应的value。

反向迭代器的实现

🚀反向迭代器就是对正向迭代器的封装，正向迭代器的++就是反向迭代器的–，反之亦然。

//反向迭代器
template<typename T>
struct __rb_tree_reverse_iterator
{using Node = T;Node _it;using Ref = typename T::_Ref;using Ptr = typename T::_Ptr;__rb_tree_reverse_iterator(T it) :_it(it) {};using self = __rb_tree_reverse_iterator<T>;bool operator==(const self& it) { return _it == it._it; }bool operator!=(const self& it) { return _it != it._it; }Ref operator*() { return *_it; }Ptr operator->() { return &operator*(); }self& operator++() { --_it; return *this; }self& operator--() { ++_it; return *this; }self operator++(int) { self tmp(*this);++tmp;return tmp;}self operator--(int){self tmp(*this);--tmp;return tmp;}
};

实现map和set

map.h

namespace gy
{template<typename K, typename V>class map{private:struct Map_KeyOfT{const K& operator()(const pair<const K, V>& kv){return kv.first;}};public:using tree = gy_rbtree::rbtree<K, pair<const K, V>, Map_KeyOfT>;using iterator = typename tree::iterator;using const_iterator = typename tree::const_iterator;using reverse_iterator = typename tree::reverse_iterator;using const_reverse_iterator = typename tree::const_reverse_iterator;public:iterator begin() { return _t.begin(); };const_iterator cbegin() { return _t.cbegin(); };iterator end() { return _t.end(); };const_iterator cend() { return _t.cend(); };reverse_iterator rbegin() { return _t.rbegin(); };const_reverse_iterator crbegin() { return _t.crbegin(); };reverse_iterator rend() { return _t.rend(); };const_reverse_iterator crend() { return _t.crend(); };pair<iterator,bool> insert(const pair<K, V>& kv) { return _t.insert(kv); }V& operator[](const K& key){pair<iterator, bool> res = insert(make_pair(key, V()));return ( * (res.first)).second;}private:tree _t;};
}

set.h

namespace gy
{template<typename K>class set{private:struct Set_KeyOfT{const K& operator()(const K& key){return key;}};public:using tree = gy_rbtree::rbtree<K, K, Set_KeyOfT>;using iterator = typename tree::iterator;using const_iterator = typename tree::const_iterator;using reverse_iterator = typename tree::reverse_iterator;using const_reverse_iterator = typename tree::const_reverse_iterator;public:iterator begin() { return _t.begin(); };const_iterator cbegin() { return _t.cbegin(); };iterator end() { return _t.end(); };const_iterator cend() { return _t.cend(); };reverse_iterator rbegin() { return _t.rbegin(); };const_reverse_iterator crbegin() { return _t.crbegin(); };reverse_iterator rend() { return _t.rend(); };const_reverse_iterator crend() { return _t.crend(); };pair<iterator,bool> insert(const K& k) { return _t.insert(k); }private:tree _t;};
}

RBTree.h

#pragma once
#include <time.h>
#include <stdlib.h>
namespace gy_rbtree
{typedef enum color{BLACK,RED}color;//红黑树结点template<typename T>struct TreeNode{public:TreeNode<T>(const T& data):_data(data), _col(RED){}public:color _col;T _data;TreeNode<T>* _left = nullptr;TreeNode<T>* _right = nullptr;TreeNode<T>* _parent = nullptr;};//正向迭代器template<typename T,typename Ref,typename Ptr>struct __rb_tree_iterator{using _Ref = Ref;using _Ptr = Ptr;using Node = TreeNode<T>;__rb_tree_iterator(Node* n) : _node(n) {};using self = __rb_tree_iterator<T, Ref, Ptr>;Node* _node;bool operator==(const self& it) { return _node == it._node; }bool operator!=(const self& it) { return _node != it._node; }Ref operator*() { return _node->_data; }Ptr operator->() { return &operator*(); }self& operator++(){Node* cur = _node;if (cur && cur->_right) // 右子树存在{cur = cur->_right;while (cur->_left) cur = cur->_left;_node = cur;}else if(cur) //右子树不存在{Node* parent = cur->_parent;while (parent && parent->_right == cur){parent = parent->_parent;cur = cur->_parent;}_node = parent;}return *this;}self& operator--(){Node* cur = _node;if (cur && cur->_left) //存在左结点{cur = cur->_left;while (cur->_right) cur = cur->_right;_node = cur;}else if (cur) //不存在左结点{Node* parent = cur->_parent;while (parent && parent->_left == cur){parent = parent->_parent;cur = cur->_parent;}_node = parent;}return *this;}self operator++(int){self tmp(*this);++tmp;return tmp;}self operator--(int){self tmp(*this);--tmp;return tmp;}};//反向迭代器template<typename T>struct __rb_tree_reverse_iterator{using Node = T;Node _it;using Ref = typename T::_Ref;using Ptr = typename T::_Ptr;__rb_tree_reverse_iterator(T it) :_it(it) {};using self = __rb_tree_reverse_iterator<T>;bool operator==(const self& it) { return _it == it._it; }bool operator!=(const self& it) { return _it != it._it; }Ref operator*() { return *_it; }Ptr operator->() { return &operator*(); }self& operator++() { --_it; return *this; }self& operator--() { ++_it; return *this; }self operator++(int) { self tmp(*this);++tmp;return tmp;}self operator--(int){self tmp(*this);--tmp;return tmp;}};//红黑树template<class K, class T,class KeyOfT>class rbtree{public:typedef TreeNode<T> node;KeyOfT _kot;using iterator = __rb_tree_iterator<T, T&, T*>;using reverse_iterator = __rb_tree_reverse_iterator<iterator>;using const_iterator = __rb_tree_iterator<T, const T&, const T*>;using const_reverse_iterator = __rb_tree_reverse_iterator<const_iterator>;public:rbtree() = default; //默认构造~rbtree() { Destroy(_root); _root = nullptr; } //析构rbtree(const rbtree& t) { _root = Copy(t._root); } //拷贝构造iterator begin(){node* cur = _root;if (_root == nullptr) return iterator(nullptr);while (cur->_left) cur = cur->_left;return iterator(cur);}const_iterator cbegin() {node* cur = _root;if (_root == nullptr) return const_iterator(nullptr);while (cur->_left) cur = cur->_left;return const_iterator(cur);}iterator end() { return iterator(nullptr); }const_iterator cend() { return const_iterator(nullptr); }reverse_iterator rbegin() {node* cur = _root;if (_root == nullptr) return reverse_iterator(iterator(nullptr));while (cur->_right) cur = cur->_right;return reverse_iterator(iterator(cur));}reverse_iterator rend() { return reverse_iterator(iterator(nullptr)); }const_reverse_iterator crbegin(){ node* cur = _root;if (_root == nullptr) return const_iterator(nullptr);while (cur->_right) cur = cur->_right;return const_reverse_iterator(const_iterator(cur));}const_reverse_iterator crend() { return const_reverse_iterator(const_iterator(nullptr)); }pair<iterator,bool> insert(const T& data){//根节点为空if (_root == nullptr){_root = new node(data);_root->_col = BLACK;return make_pair(iterator(_root),true);}node* cur = _root;node* parent = nullptr;while (cur){if (_kot(cur->_data) > _kot(data)){parent = cur;cur = cur->_left;}else if (_kot(cur->_data) < _kot(data)){parent = cur;cur = cur->_right;}else{//已经存在了return make_pair(iterator(cur),false);}}//找到了属于它的位置,插入cur = new node(data);node* ret = cur;cur->_parent = parent;if (_kot(data) < _kot(parent->_data)){parent->_left = cur;}else{parent->_right = cur;}//只要parent结点存在，并且其结点为颜色为红色就需要调整while (parent && parent->_col == RED){node* grandfather = parent->_parent;if (parent == grandfather->_left){//1,第一种情况，存在叔叔结点，并且为红色if (grandfather->_right && grandfather->_right->_col == RED){//祖父结点变红，父亲结点和叔叔结点变黑，继续向上调整，直到根节点为止。grandfather->_col = RED;parent->_col = BLACK;grandfather->_right->_col = BLACK;cur = grandfather;parent = cur->_parent;}//2,叔叔结点不存在或者为黑色else{//2.1 cur为parent的左子树，那么只需要祖父为根的树右旋即可if (cur == parent->_left){grandfather->_col = RED;parent->_col = BLACK;RotateR(grandfather);}//2.2 cur为parent的右子树，那么先对parent左旋，在对祖父右旋else if (cur == parent->_right){grandfather->_col = RED;cur->_col = BLACK;RotateLR(grandfather);}break;}}else{if (grandfather->_left && grandfather->_left->_col == RED){grandfather->_col = RED;parent->_col = BLACK;grandfather->_left->_col = BLACK;cur = grandfather;parent = cur->_parent;}else{if (cur == parent->_right){grandfather->_col = RED;parent->_col = BLACK;RotateL(grandfather);}else if (cur == parent->_left){grandfather->_col = RED;cur->_col = BLACK;RotateRL(grandfather);}break;}}}_root->_col = BLACK;return make_pair(iterator(ret),true);}private:void RotateL(node* parent){node* subR = parent->_right;node* subRL = subR->_left;parent->_right = subRL;if (subRL){subRL->_parent = parent;}subR->_left = parent;node* ppnode = parent->_parent;parent->_parent = subR;if (ppnode == nullptr){_root = subR;subR->_parent = nullptr;}else if (ppnode->_left == parent){ppnode->_left = subR;subR->_parent = ppnode;}else{ppnode->_right = subR;subR->_parent = ppnode;}}void RotateR(node* parent){node* subL = parent->_left;node* subLR = subL->_right;parent->_left = subLR;if (subLR){subLR->_parent = parent;}subL->_right = parent;node* ppnode = parent->_parent;parent->_parent = subL;if (ppnode == nullptr){_root = subL;subL->_parent = nullptr;}else if (ppnode->_left == parent){ppnode->_left = subL;subL->_parent = ppnode;}else{ppnode->_right = subL;subL->_parent = ppnode;}}void RotateLR(node* parent){node* subL = parent->_left;RotateL(subL);RotateR(parent);}void RotateRL(node* parent){node* subR = parent->_right;RotateR(subR);RotateL(parent);}void Destroy(node* root){if (root == nullptr) return;Destroy(root->_left);Destroy(root->_right);delete root;}node* Copy(node* root){if (root == nullptr) return;node* newroot = new node(root->_kv);newroot->_left = Copy(root->_left);newroot->_right = Copy(root->_right);return newroot;}private:node* _root = nullptr;};}