阿尔法贝塔剪枝——中国象棋人机对战

alpha-beta剪枝算法实现中国象棋人机对战

Github仓库：https://github.com/dick20/Artificial-Intelligence

问题介绍

本实验要求编写一个中国象棋博弈程序，使用alpha-beta剪枝算法，实现人机对弈。因为是人机博弈，因此我们需要使得电脑比较聪明，而方法就是要电脑选择走比较好的步骤。机器是基于搜索来下棋的，我们需要让机器考虑比较长远的情况，然后做出比较好的选择，而为了提高搜索效率，就应用到了alpha-beta剪枝算法。

算法介绍

对于博弈问题，我们首先考虑的是极小极大搜索算法。我们规定：MAX代表程序方，MIN代表对手方，P代表一个棋局（即一个状态）。有利于MAX的势态， $f (P)$ 取正值；有利于MIN的势态， $f (P)$ 取负值；势态均衡， $f (P)$ 取零。 $f (P)$ 的大小由棋局势态的优劣来决定。评估棋局的静态函数要考虑两个方面的因素：

双方都知道自己走到了什么程度
双方都知道下一步能够做什么

基于这个前提，博弈双方要考虑的问题是：如何产生一个最好的走步，能尽快获胜。因此，就引出来极小极大搜索算法。

极小极大搜索的基本思想是：

当轮到MIN走步的节点时，MAX应考虑最坏的情况（因此， $f (P)$ 取极小值）。
当轮到MAX走步的节点时，MAX应考虑最好额情况（因此， $f (P)$ 取极大值）。
当评价往回倒退时，相应于两位棋手的对抗策略，不同层上交替地使用1、2两种方法向上传递倒推值。

MIN、MAX过程将生成后继节点与估计格局两个过程分开考虑，即需要先生成全部搜索树，然后再进行每个节点的静态估计和倒推值计算。实际上，这种方法效率极低。而alpha-beta基于这个过程，给了我们一个高效的算法。在极大层中定义下界值 $\alpha$ ，它表明该MAX节点向上的倒推值不会小于 $\alpha$ ；在极小层中定义上界值 $\beta$ ，它表明该MIN节点向上的倒推值不会大于 $\beta$ 。

剪枝规则如下：

$\alpha$ 剪枝。若任一极小层节点的 $\beta$ 值不大于它任一前驱极大层节点的 $\alpha$ 值，即 $\alpha$ （前驱层） $\ge \beta$ （后继层），则可以中止该极小层中这个MIN节点以下的搜索过程。这个MIN节点最终的倒推值就确定为这个 $\beta$ 值。
$\beta$ 剪枝。若任一极大层节点的 $\alpha$ 值不小于它任一前驱极小层节点的 $\beta$ 值，即 $\alpha$ （后继层） $\ge \beta$ （前驱层），则可以中止该极大层中这个MAX节点以下的搜索过程。这个MAX节点最终的倒推值就确定为这个 $\alpha$ 值。

算法实现

本次项目的UI是参考了网上的代码，使用Java实现。重点分析alpha-beta剪枝算法，关于UI部分就不详细分析了。

首先我们来看棋局的评估，能否对棋局有一个好的评估是这个算法很关键的一环。我们需要对棋局做出合适的评估，以确定最好的走步。评估的方面有三个，一个是下一步的棋力，第二个是下一步能做什么，第三个是棋子的价值。先看棋力，棋力的评估主要是根据棋子所在的位置来分析。这里我们写好了每个棋子在不同位置的棋力，这是参考了一些论文得出来的。第二个是下一步能做什么，我们可以根据下一步能做什么来判断这个走步的好坏。在象棋游戏中，一个好的走步我们期望是能够吃掉对方的棋，而且吃掉的棋子价值越大，这个走步越好。当然，如果下一步能够将军，那么这个走步很有可能就是我们想要的。于是我们对下一步能做什么做一个估值：如果下一步能将军，那么它的估值将大大增加（+9999）；如果下一步能吃掉对方的棋子，那么它的估值将会有一定的增加（车：+500，马或炮：+100）；如果下一步只能吃掉对方的卒，那么它的估值就会下降（-20），因为多数情况下吃掉对方的卒都没什么好处。最后是棋子的价值，这是比较固定的因素，因为我们普遍认为某些棋子的价值是比其他棋子大的（比如车的价值一般来说都比卒要大）。

每次估值都需要分开两方的棋子来进行估值。即算出程序方棋局的总体价值和对手方棋局的整体价值。用程序方估值-对手方估值作为这个状态下的估值。如果这个估值大于0，说明程序方占优势；反之，说明对手方占优势。

完成好估值后，就可以开始alpha-beta的剪枝算法了。首先确定博弈树的深度，通俗来说就是要让程序往后推演几步。当然推演的步数越多，越能找到一个好的走步，但是所需的时间也就越多。然后我们需要使用一个标记来表示当前是极大层还是在极小层，根据标记来计算当前节点的 $\alpha$ 或 $\beta$ 。如果在极大层，我们需要获得它下面所有极小层的倒推值的极大值（实际上不是所有）；如果在极小层，就需要获得它下面所有极大层的倒推层的极小值（实际上不是所有）。这里就牵涉到了剪枝。以在极大层为例，如果当前MAX节点提供的倒推值 $\alpha$ 大于其前驱极小层MIN节点的 $\beta$ ，那么说明这个MAX节点以下搜索提供的值不可能小于 $\alpha$ ，也就没有继续搜索的意义了，所以就可以直接结束这个MAX节点的搜索，这就是剪枝。

关键代码分析

棋子本身的价值评估：

int[] BasicValue = { 80, 0, 0, 300, 500, 300, 100};

将军：80
士：0
象：0
马：300
车：500
炮：300
卒：100

棋子位置的价值评估：

将军

int[][] JiangPosition = new int[][] {{0, 0, 0, 1, 5, 1, 0, 0, 0},{0, 0, 0, -8, -8, -8, 0, 0, 0},{0, 0, 0, -9, -9, -9, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0, 0}};

士

int[][] ShiPosition = new int[][] {{0, 0, 0, 0, 0, 0, 0, 0, 0},{0, 0, 0, 0, 3, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0, 0}};

象

int[][] XiangPosition = new int[][] {{0, 0, 0, 0, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0, 0},{-2, 0, 0, 0, 3, 0, 0, 0, -2},{0, 0, 0, 0, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0, 0}};

马

int[][] MaPosition = new int[][] {{0, -3, 2, 0, 2, 0, 2, -3, 0},{-3, 2, 4, 5, -10, 5, 4, 2, -3},{5, 4, 6, 7, 4, 7, 6, 4, 5},{4, 6, 10, 7, 10, 7, 10, 6, 4},{2, 10, 13, 14, 15, 14, 13, 10, 2},{2, 10, 13, 14, 15, 14, 13, 10, 2},{2, 12, 11, 15, 16, 15, 11, 12, 2},{5, 20, 12, 19, 12, 19, 12, 20, 5},{4, 10, 11, 15, 11, 15, 11, 10, 4},{2, 8, 15, 9, 6, 9, 15, 8, 2},{2, 2, 2, 8, 2, 8, 2, 2, 2}};

车

int[][] JuPosition = new int[][] {{-6, 6, 4, 12, 0, 12, 4, 6, -6},{5, 8, 6, 12, 0, 12, 6, 8, 5},{-2, 8, 4, 12, 12, 12, 4, 8, -2},{4, 9, 4, 12, 14, 12, 4, 9, 4},{8, 12, 12, 14, 15, 14, 12, 12, 8},{8, 11, 11, 14, 15, 14, 11, 11, 8},{6, 13, 13, 16, 16, 16, 13, 13, 6},{6, 8, 7, 14, 16, 14, 7, 8, 6},{6, 12, 9, 16, 33, 16, 9, 12, 6},{6, 8, 7, 13, 14, 13, 7, 8, 6}};

炮

int[][] PaoPosition = new int[][] {{0, 0, 1, 3, 3, 3, 1, 0, 0},{0, 1, 2, 2, 2, 2, 2, 1, 0},{1, 0, 4, 3, 5, 3, 4, 0, 1},{0, 0, 0, 0, 0, 0, 0, 0, 0},{-2, 0, -2, 0, 6, 0, -2, 0, -2},{3, 0, 4, 0, 7, 0, 4, 0, 3},{10, 18, 22, 35, 40, 35, 22, 18, 10},{20, 27, 30, 40, 42, 40, 30, 27, 20},{20, 30, 45, 55, 55, 55, 45, 30, 20},{20, 30, 50, 65, 70, 65, 50, 30, 20},{0, 0, 0, 2, 4, 2, 0, 0, 0}};

卒

int[][] BingPosition = new int[][] {{0, 0, 0, 0, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0, 0},{0, 0, 0, 0, 0, 0, 0, 0, 0},{-2, 0, -2, 0, 6, 0, -2, 0, -2},{3, 0, 4, 0, 7, 0, 4, 0, 3},{10, 18, 22, 35, 40, 35, 22, 18, 10},{20, 27, 30, 40, 42, 40, 30, 27, 20},{20, 30, 50, 65, 70, 65, 50, 30, 20},{0, 0, 0, 2, 4, 2, 0, 0, 0}};

对下一步吃子进行估值：

private int estimate_myself(Piece piece) {// System.out.println(piece.Info);if (piece.Info == "bb0" || piece.Info == "rb0") return 0;int totalValue = 0;ArrayList<int[]> next = Rule.getNextMove(piece.Info, piece.pos, Board);for (int[] n : next) {Piece p = Board.getPiece(n);if (p != null && Board.getPiece(n).character == 'b') {totalValue += 9999;break;}if (p != null && Board.getPiece(n).character == 'j') {totalValue += 500;break;}if (p != null && Board.getPiece(n).character == 'm' &&  Board.getPiece(n).character == 'p') {totalValue += 100;}if (p != null && Board.getPiece(n).character == 'z') {totalValue -= 20;}}return totalValue;}

下一步能将军，估值+9999（相当于直接选择这个值了）
下一步能吃【车】，估值+500
下一步能吃【马】或【炮】，估值+100
下一步能吃【卒】，估值-20

对每个状态的估值

public int estimate(ChessBoard Board) {int[][] totalValue = new int[2][3];for (Map.Entry<String, Piece> pieceEntry : Board.pieces.entrySet()) {Piece piece = pieceEntry.getValue();switch (piece.character) {case 'b':if (piece.color == 'b') {totalValue[0][0] += estimate_value(0);totalValue[0][1] += estimate_position(0, piece.pos);} else {totalValue[1][0] += estimate_value(0);totalValue[1][1] += estimate_position(0, getOppositePos(piece.pos));}break;case 's':if (piece.color == 'b') {totalValue[0][0] += estimate_value(1);totalValue[0][1] += estimate_position(1, piece.pos);} else {totalValue[1][0] += estimate_value(1);totalValue[1][1] += estimate_position(1, getOppositePos(piece.pos));}break;case 'x':if (piece.color == 'b') {totalValue[0][0] += estimate_value(2);totalValue[0][1] += estimate_position(2, piece.pos);} else {totalValue[1][0] += estimate_value(2);totalValue[1][1] += estimate_position(2, getOppositePos(piece.pos));}break;case 'm':if (piece.color == 'b') {totalValue[0][0] += estimate_value(3);totalValue[0][1] += estimate_position(3, piece.pos);} else {totalValue[1][0] += estimate_value(3);totalValue[1][1] += estimate_position(3, getOppositePos(piece.pos));}break;case 'j':if (piece.color == 'b') {totalValue[0][0] += estimate_value(4);totalValue[0][1] += estimate_position(4, piece.pos);} else {totalValue[1][0] += estimate_value(4);totalValue[1][1] += estimate_position(4, getOppositePos(piece.pos));}break;case 'p':if (piece.color == 'b') {totalValue[0][0] += estimate_value(5);totalValue[0][1] += estimate_position(5, piece.pos);} else {totalValue[1][0] += estimate_value(5);totalValue[1][1] += estimate_position(5, getOppositePos(piece.pos));}break;case 'z':if (piece.color == 'b') {totalValue[0][0] += estimate_value(6);totalValue[0][1] += estimate_position(6, piece.pos);} else {totalValue[1][0] += estimate_value(6);totalValue[1][1] += estimate_position(6, getOppositePos(piece.pos));}break;}totalValue[0][2] += estimate_myself(piece);totalValue[1][2] += estimate_myself(piece);}int red = totalValue[1][0] + totalValue[1][1] + totalValue[1][2];int black = totalValue[0][0] + totalValue[0][1] + totalValue[0][2];int result_value = black - red;return result_value;}

对每个状态的估值包含了上面三种估值，然后用程序方估值-对手方估值得出最终结果。

alpha-beta剪枝算法。

// alpha-beta algorithm.private int alpha_beta_search(int depth, int alpha, int beta, boolean isMax) {// Recursion end: if the depth is 0 or Gameover.if (depth == 0 || controller.hasWin(Board) != 'x') {return estimate(Board);}// Generate all the situation the current position will go.// 只有在极大值层的时候才会生成ArrayList<AlphaBetaNode> allNextStep = new ArrayList<AlphaBetaNode>();for (Map.Entry<String, Piece> entry : Board.pieces.entrySet()) {Piece piece = entry.getValue();if ((piece.color == 'b' && isMax) || (piece.color == 'r' && !isMax)) {for (int[] next : Rule.getNextMove(piece.Info, piece.pos, Board)) {AlphaBetaNode newNode = new AlphaBetaNode(piece.Info, piece.pos, next);allNextStep.add(newNode);}}}for (AlphaBetaNode n : allNextStep) {Piece Eaten_piece = Board.updatePiece(n.piece_key, n.to);if (isMax) {alpha = Math.max(alpha, alpha_beta_search(depth-1, alpha, beta, false));} else {beta = Math.min(beta, alpha_beta_search(depth-1, alpha, beta, true));}Board.updatePiece(n.piece_key, n.from);if (Eaten_piece != null) {Board.pieces.put(Eaten_piece.Info, Eaten_piece);Board.backPiece(Eaten_piece.Info);}// 剪枝过程if (beta <= alpha) break;}	return isMax ? alpha : beta;}

整个剪枝算法是自顶向下的，所以要判断层数，当depth=0时，说明已经到叶子节点，直接返回当前节点的估值。使用一个isMax布尔变量标记当前是极大层还是极小层，在当前节点下生成所有可能的后继节点，对每个节点进行极小极大搜索。每个子节点倒推 $\alpha$ 或 $\beta$ ，然后根据isMax去求极大或极小。每完成一个节点，就试图去做剪枝。极大层返回alpha，极小层返回beta。

然后封装一个函数给外部调用。这个函数向外部返回的是估值最好的一个走步。

public AlphaBetaNode search(ChessBoard board) {this.Board = board;ArrayList<AlphaBetaNode> allNextStep = new ArrayList<AlphaBetaNode>();for (Map.Entry<String, Piece> entry : Board.pieces.entrySet()) {Piece piece = entry.getValue();if (piece.color == 'b') {for (int[] next : Rule.getNextMove(piece.Info, piece.pos, Board)) {AlphaBetaNode newNode = new AlphaBetaNode(piece.Info, piece.pos, next);allNextStep.add(newNode);}				}}AlphaBetaNode best = null;for (AlphaBetaNode n : allNextStep) {Piece p = Board.getPiece(n.to);if (p != null && p.character == 'b') {return n;}}long start = System.currentTimeMillis();for (AlphaBetaNode n : allNextStep) {Piece eaten = Board.updatePiece(n.piece_key, n.to);if (eaten != null) n.value += 100;n.value = alpha_beta_search(depth, Integer.MIN_VALUE, Integer.MAX_VALUE, false);if (best == null || n.value >= best.value) {best = n;}Board.updatePiece(n.piece_key, n.from);if (eaten != null) {board.pieces.put(eaten.Info, eaten);board.backPiece(eaten.Info);}}long finish = System.currentTimeMillis();System.out.println("Calculate Time: " + (finish-start) + "ms");System.out.println("From: (" + best.from[0] + ", " + best.from[1] + ") to (" + best.to[0] + ", " + best.to[1] + ")");return best;}

对于每一个棋局，将所有的走步都变成一个节点，然后对每一个走步使用alpha-beta剪枝算法进行极小极大搜索。注意，如果下一步有将军的走步，直接作为最优节点返回。

测试与分析

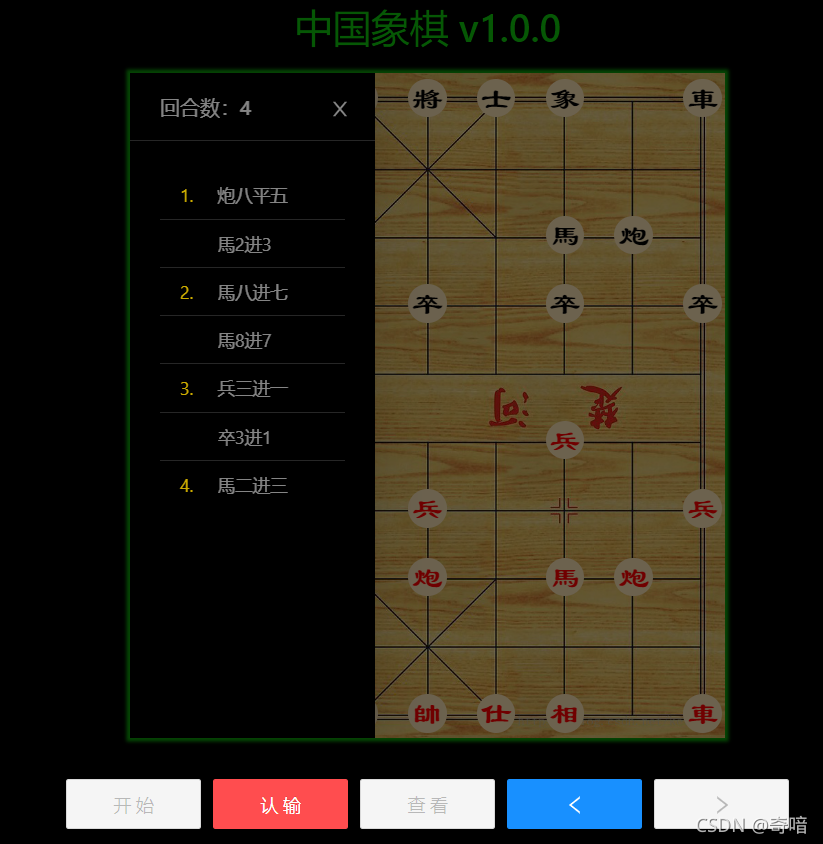
初始界面

走了第一步，红方中炮，黑方上马：

第一步

第二步，红方用炮吃掉黑方的卒后，黑方的马会吃掉炮：

第二步

若干步后，黑方炮处于将军状态：

将军状态

如果红方不做出回应，黑方会直接将军，游戏获胜：

黑方获胜

测试过程中需要不断调整棋局估算的参数，经过多次测试，当前的这个参数是比较智能的一个状态了。

分析：从一些运行结果来看，程序方还是具有一定的智能的。因为时间效率问题，这里只实现了两层的博弈树，如果玩家水平比较不错的话，程序方一般是比较难获胜的。

总结

相比起极小极大搜索法，alpha-beta剪枝算法得到的结果是完全相同的，它并没有在搜索解上有更加好的结果，但是，MIN、MAX要将整个图都搜索完毕，而alpha-beata剪枝算法只需要搜索其中的部分节点，所以它具有更高的效率。因此，给定相同的时间，alpha-beta能够搜索更深的深度，因而能够获得更好的走步。

这里再给出一些日后优化的思路。一个是可以加深博弈树的层数，两层显然还是比较简单，基本不能战胜玩家。而四层却会需要大量的时间。一个比较好的方法是，对于那些明显比较有优势的走步，我们不需要看其它的走步，直接就选择这一步。比方说，如果当前走步是能够吃掉对方的车，那么很大概率上这都是一个很好的走步，因此我就不需要管后面的事情了，也相当于是一个基于启发式函数的剪枝。当然，具体的实现还要经过大量的测试才行。希望假期能有时间，继续把这个项目完善。