前言

具体的性质：

• 非对称加密算法
• 应用于一些技术标准中，如数字签名标准（DSS）、S/MIME 电子邮件标准
• 算法定义在任何循环群 G 上，安全性取决于 G 上的离散对数难题

1. 原理

主要由三部分组成：密钥生成、加密和解密

可以用这幅图讲解：（用公钥加密，私钥解密）：

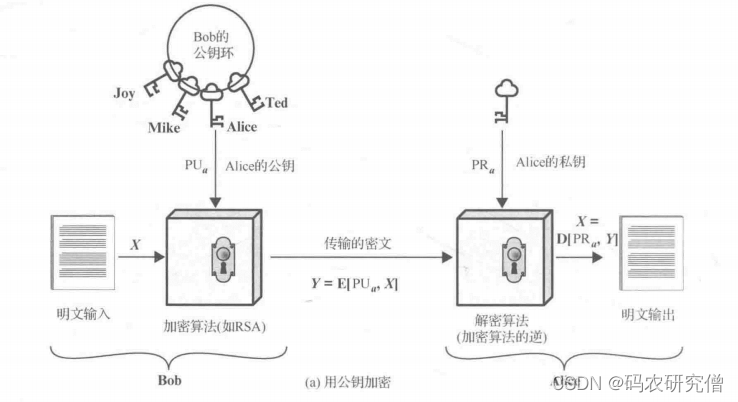
该算法与Difffie-Hellman一样，ElGamal的系统用户共同选择一个素数 q，a 是 q 的素根。

一、密钥生成：（用户A）

1. 随机生成 整数X （1< X < q - 1）
2. 计算 公钥Y = a ^X mod q

可以得到私钥 X，公钥 {q，a，Y}

二、加密：(用户B通过A的公开密钥进行加密)

1. 发送信息为 整数 M（1 $\le$ X $\le$ q - 1），以分组密码序列的方式来发送信息，其中每个分块的长度不小于整数 q
2. 取任意整数 小写k（1 $\le$ k $\le$ q - 1）
3. 取一次密钥 大写K ：K = ( Y ) ^k mod q
4. 将 整数M 加密成 明文对(C₁,C₂)，C₁ = a^k mod q ，C₂ = KM mod q

三、解密：(用户A恢复密文)

1. 计算密钥 大写K ：K = (C₁)^X mod q
2. 计算 整数M，M = (C₂K^-1) mod q

至于解密的式子 是这样生成：

式子一：
K = ( Y ) ^k mod q
K = ( a ^X mod q ) ^k mod q
K = a ^kX mod q
K = (C₁)^X mod q


式子二：
因为 C₂ = KM mod q
所以 (C₂K^-1) mod q = KMK^-1 mod q = M mod q = M

2. 例题

2.1 例题一

题目： 已知素数q为19，素根有 {2,3,10,13,14,15} ，此处 选择a = 10。

答案：

一、秘钥生成：（用户A）

1. 选择X = 5
2. 计算 Y = a ^X mod q = 10 ⁵ mod 19 = 3

A用户的 私钥 为5， 公钥为 {q,a,Y} = {19,10,3}

二、加密：(用户B通过A的公开密钥进行加密)

1. 发送消息17，想选择 小写k = 6
2. 计算 大写K ：K = ( Y ) ^k mod q = 3⁶ mod 19 = 729 mod 19 = 7
3. 密文 C₁ = a^k mod q = 10⁶ mod 1 = 11 ，C₂ = KM mod q = 7 x 17 mod 19 = 119 mod 19 =5
4. 发送密文 M = （11,5）

三、解密：(用户A恢复密文)

1. 计算 大写K ，K = (C₁)^X mod q = 11⁵ mod 19 = 7
2. K^-1 为 7^-1 mod 19 = 11
3. 最终 M = (C₂K^-1) mod q = 5 x 11 mod 19 = 55 mod 19 = 17

2.2 例题二

题目： 素数 37，取素数根，最小为2

答案：

过程与上面类似，此处讲解下具体步骤

一、秘钥生成：（用户A）
随机取一个数，取X 为 5，Y = 2 ⁵ mod 37 = 32

二、加密：(用户B通过A的公开密钥进行加密)
发送29消息，取 小写k 为 7
计算出的 大写K 为 19
C₁ = 17，C₂ = 33
M = （17,33）

三、解密：(用户A恢复密文)
大写K为 19
M 为 29