🍁博主简介
🏅云计算领域优质创作者
🏅华为云开发者社区专家博主
🏅阿里云开发者社区专家博主
💊交流社区:运维交流社区 欢迎大家的加入!
文章目录
- 一、下载maven包
- 方法一:官网下载包
- 方法二:wget直接下载
- 二、配置环境变量
- 三、mvn校验
一、下载maven包
- 下载有两种方法,分为:官网下载包和wget直接下载
方法一:官网下载包
- 1、登录网址查看下载源:清华大学开源软件镜像站
- 2、搜索apache

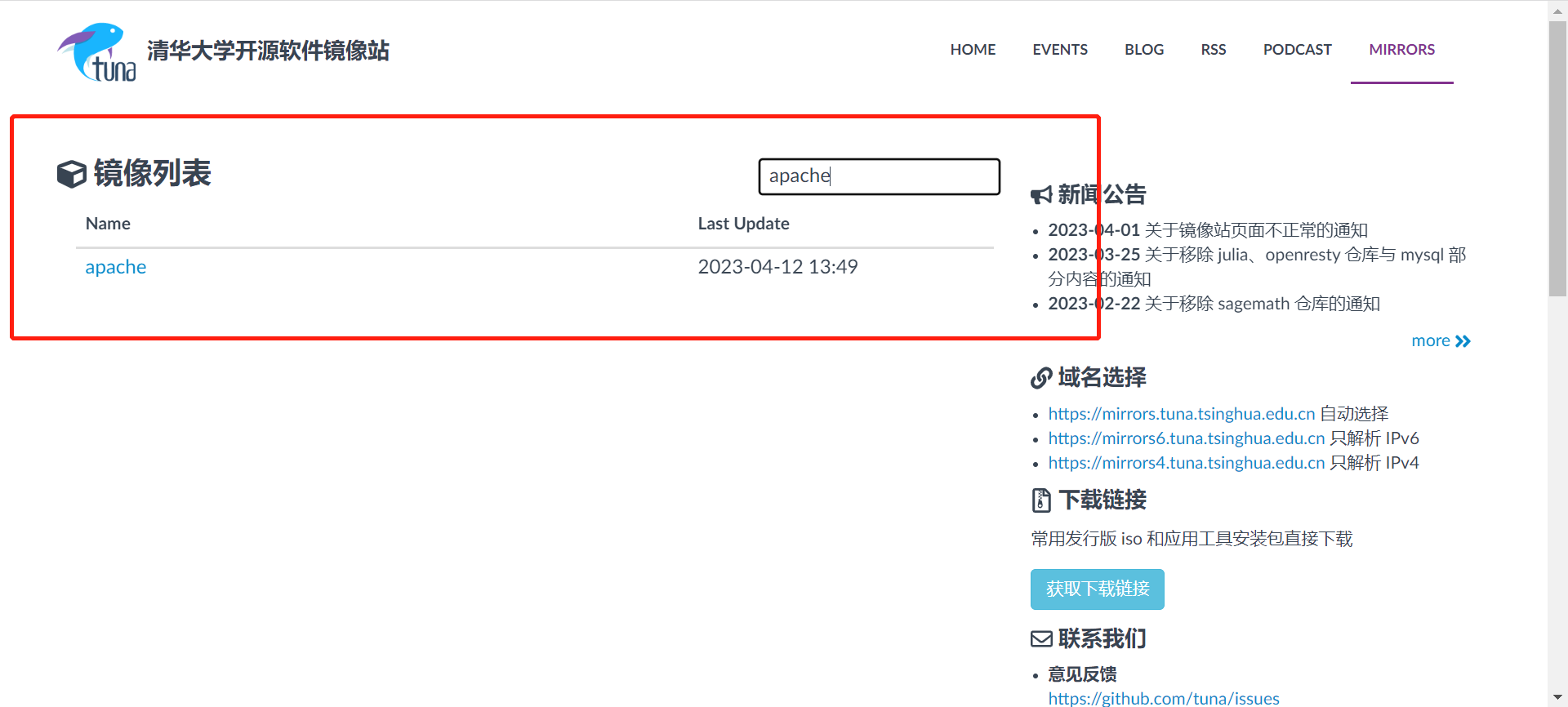
- 3、进入apache,找到maven并下载,可使用
ctrl+f搜索

- 4、点击进入选择自己所需版本,外面是大版本,里面还有小版本

- 5、我就点击最新的maven-4,进入之后在点击
4.0.0-alpha-5,在选择binaries,选择自己想要下载包格式,我选择的是zip格式
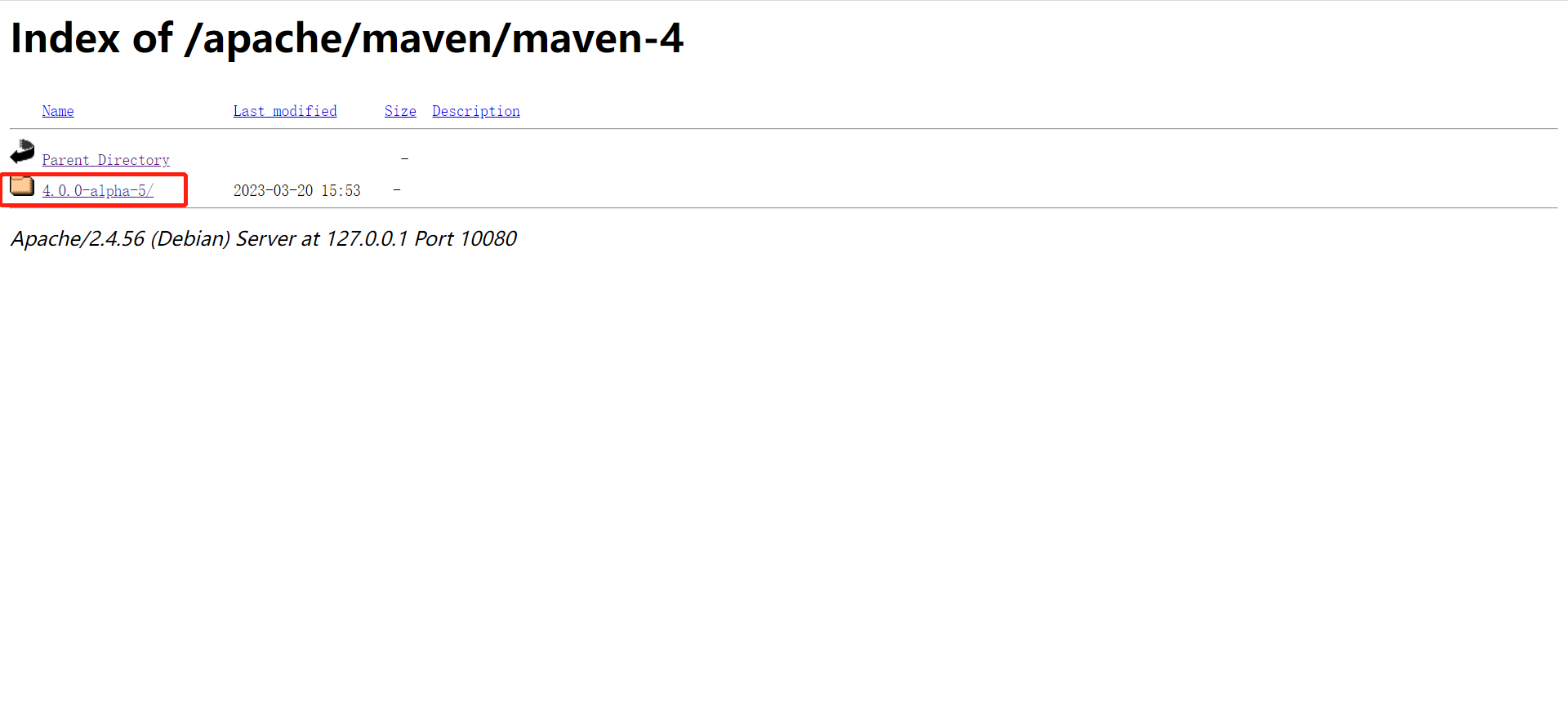
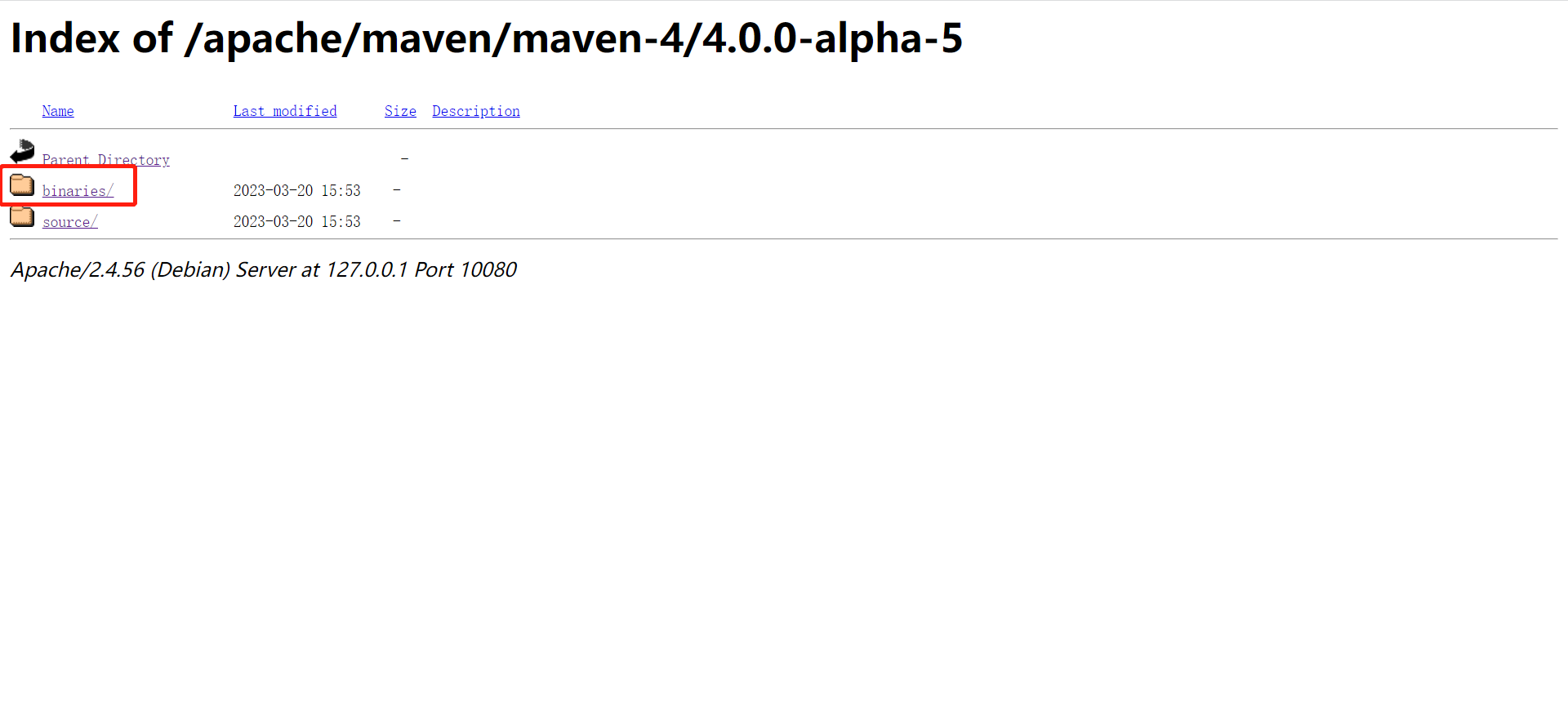
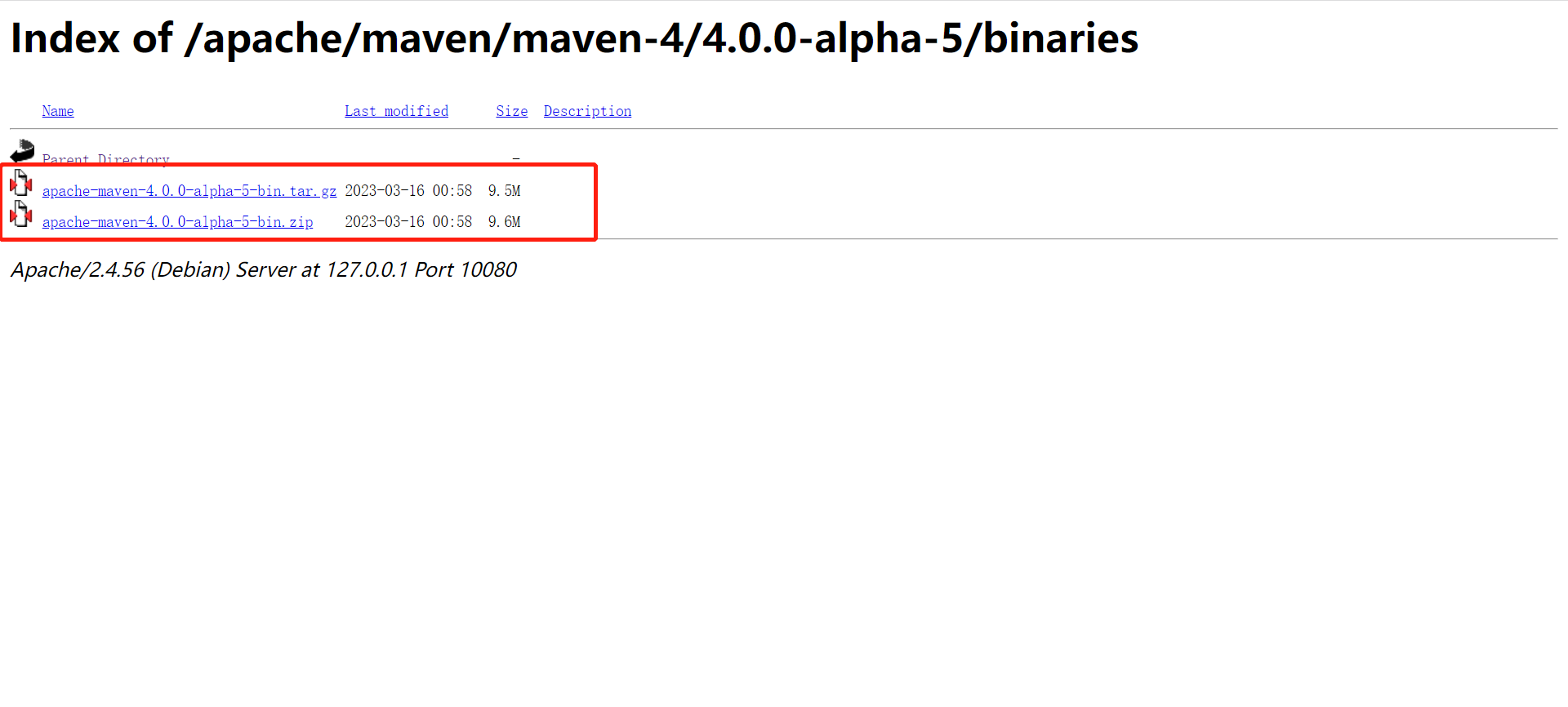
这是下载地址:https://mirrors.tuna.tsinghua.edu.cn/apache/maven/maven-4/4.0.0-alpha-5/binaries/
- 6、下载完成之后上传到服务器上解压即可。
完了在配置环境变量,生效就可以用了,具体可以看下面操作: 配置环境变量。
方法二:wget直接下载
可以复制上面找到的路径进入,然后点击自己想要下载的包的格式,右击复制连接,完成之后在linux服务器上直接使用wget下载。
这是下载地址:https://mirrors.tuna.tsinghua.edu.cn/apache/maven/maven-4/4.0.0-alpha-5/binaries/
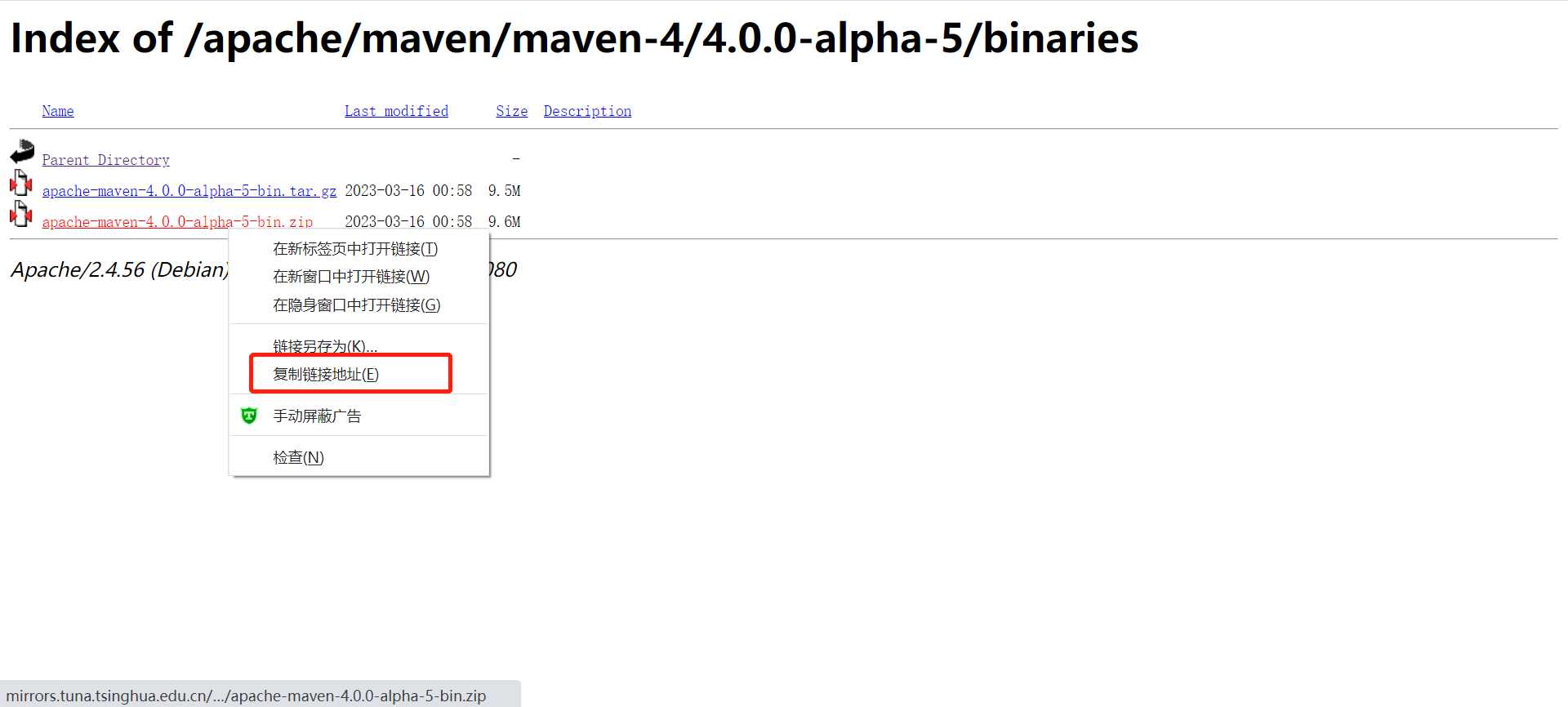
#创建maven目录
mkdir -p /usr/local/maven#进入/usr/local/maven目录
cd /usr/local/maven#拉取maven包
wget https://mirrors.tuna.tsinghua.edu.cn/apache/maven/maven-4/4.0.0-alpha-5/binaries/apache-maven-4.0.0-alpha-5-bin.zip
二、配置环境变量
- 1、解压下载的包
unzip apache-maven-4.0.0-alpha-5-bin.zip
- 2、配置环境变量:编辑/etc/profile文件
vim /etc/profile
- 3、在文件中添加,注意将MAVEN_HOME的值改成自己文件夹。
MAVEN_HOME=/usr/local/maven/apache-maven-4.0.0-alpha-5
export PATH=${MAVEN_HOME}/bin:${PATH}
- 4、生效配置文件
source /etc/profile
三、mvn校验
mvn -v
当你看到如下内容,那么恭喜你成功了,如果你没有装jdk会提示你找不到jdk;报错如下下。

该报错是找不多jdk,配置一个jdk即可;可参考:Linux中安装jdk1.8和配置环境变量 来配置jdk,配置完成之后再次执行以下mvn -v校验即可。


![[2019.01.24]JNI经验积累](https://img-blog.csdnimg.cn/7516100b75f446b29da86e26a5bf453f.png)