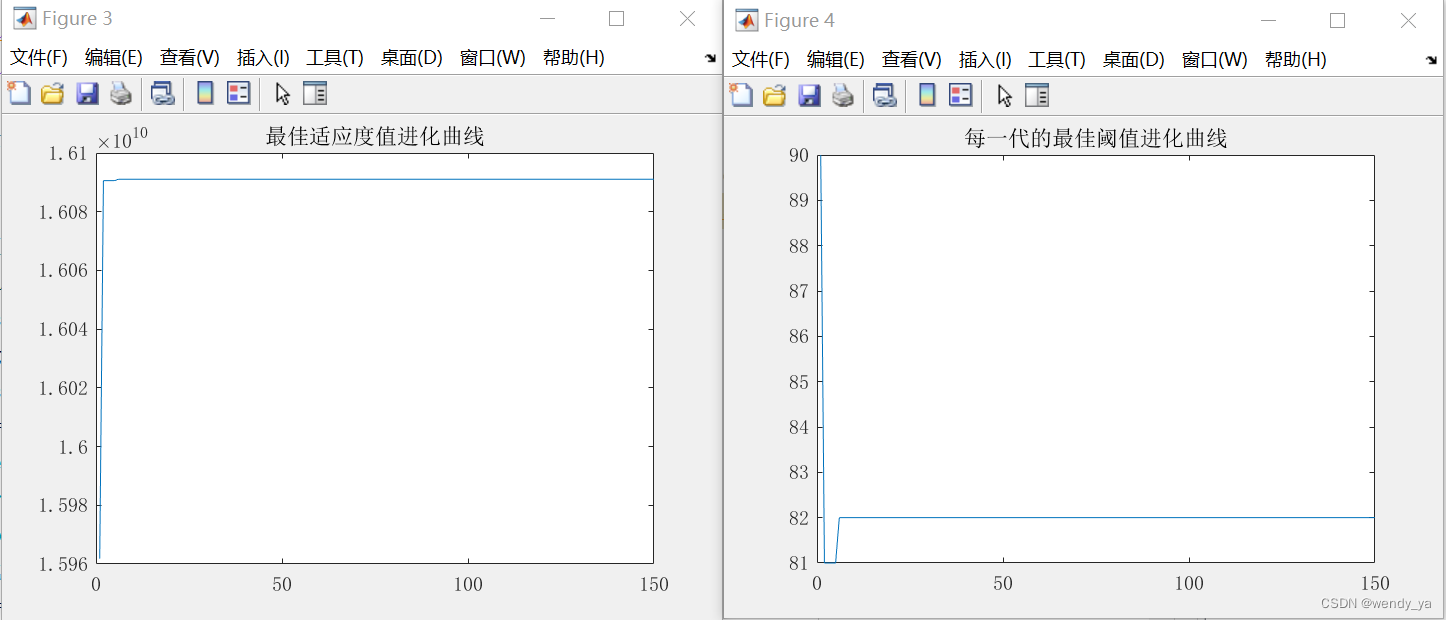
加油加油,五一前复习玩,五一就可以出去玩啦
一、状态空间法(State Space Representation)
问题求解技术主要是两个方面
- 问题的表示
- 求解的方法
状态空间法
- 状态
- 算符
- 状态空间方法
1.1 问题状态描述
定义
- 状态:描述某类不同事物间的差别而引入的一组最少变量q0,q1,…,qn的有序集合。
- 算符:使问题从一种状态变化为另一种状态的手段称为操作符或算符。
- 问题的状态空间:是一个表示该问题全部可能状态及其关系的图,它包含三种说明的集合,即三元状态(S,F,G)。
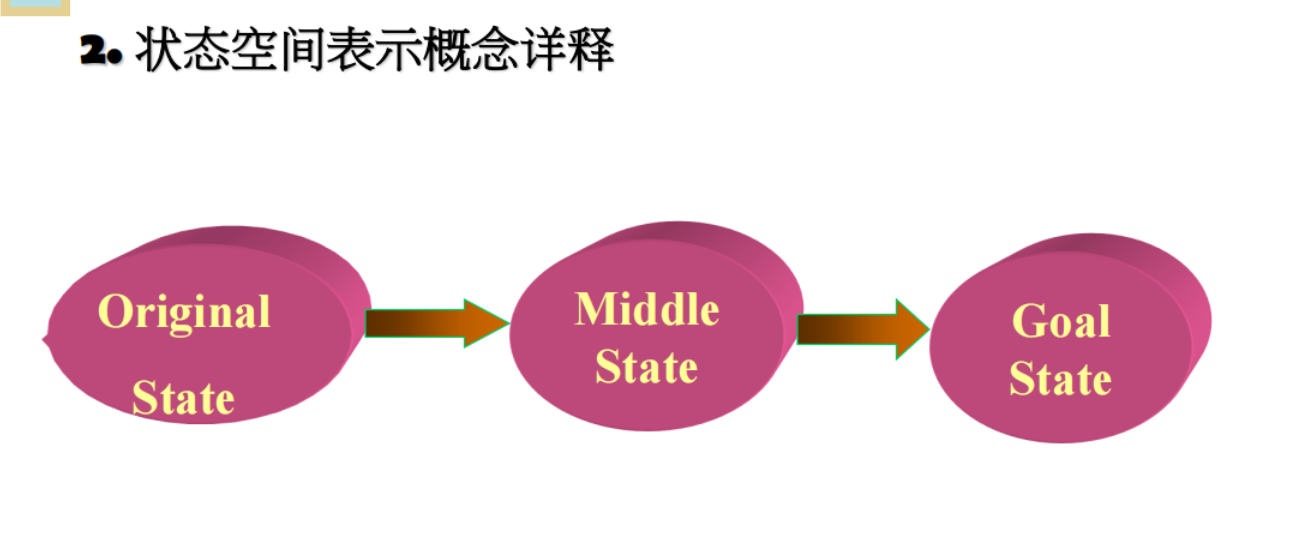
1.2 状态图示法
有向图
路径
代价
图的显示说明
图的隐示说明
1.3 状态空间表示举例
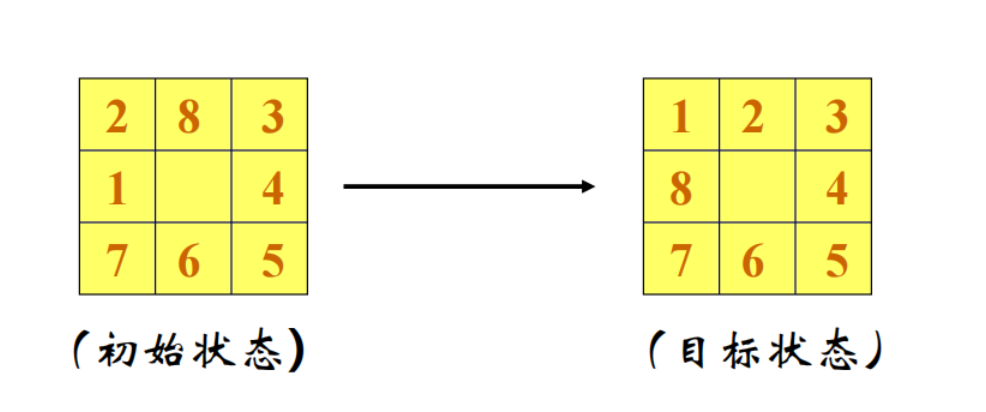
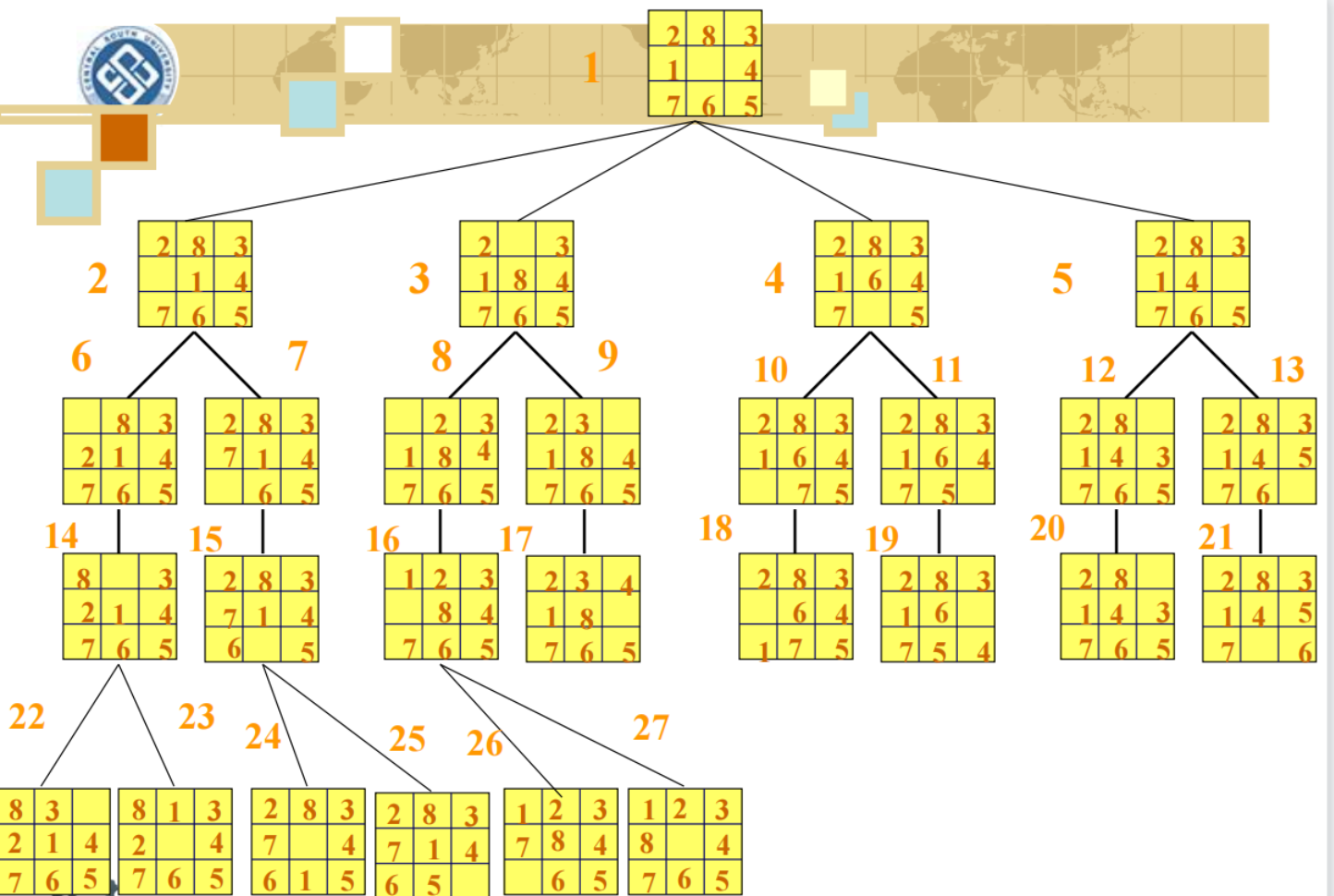
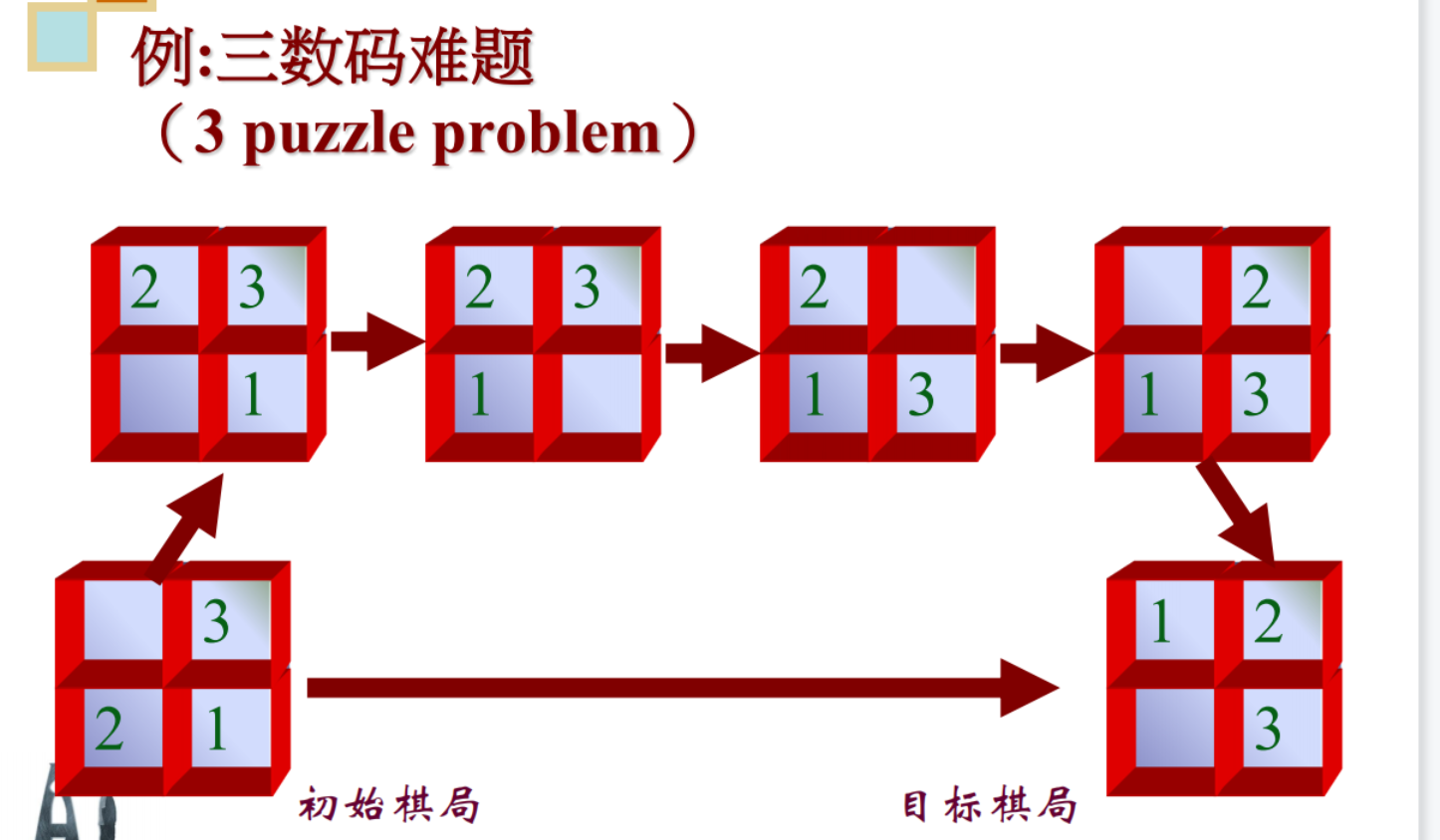
1.3.1 八数码难题
在3×3的棋盘,摆有八个棋子,每个棋子上标有1至8的某一数字。棋盘上还有一个空格,与空格相邻的棋子可以移到空格中。
如何将棋盘从某一初始状态变成最后的目标状态?
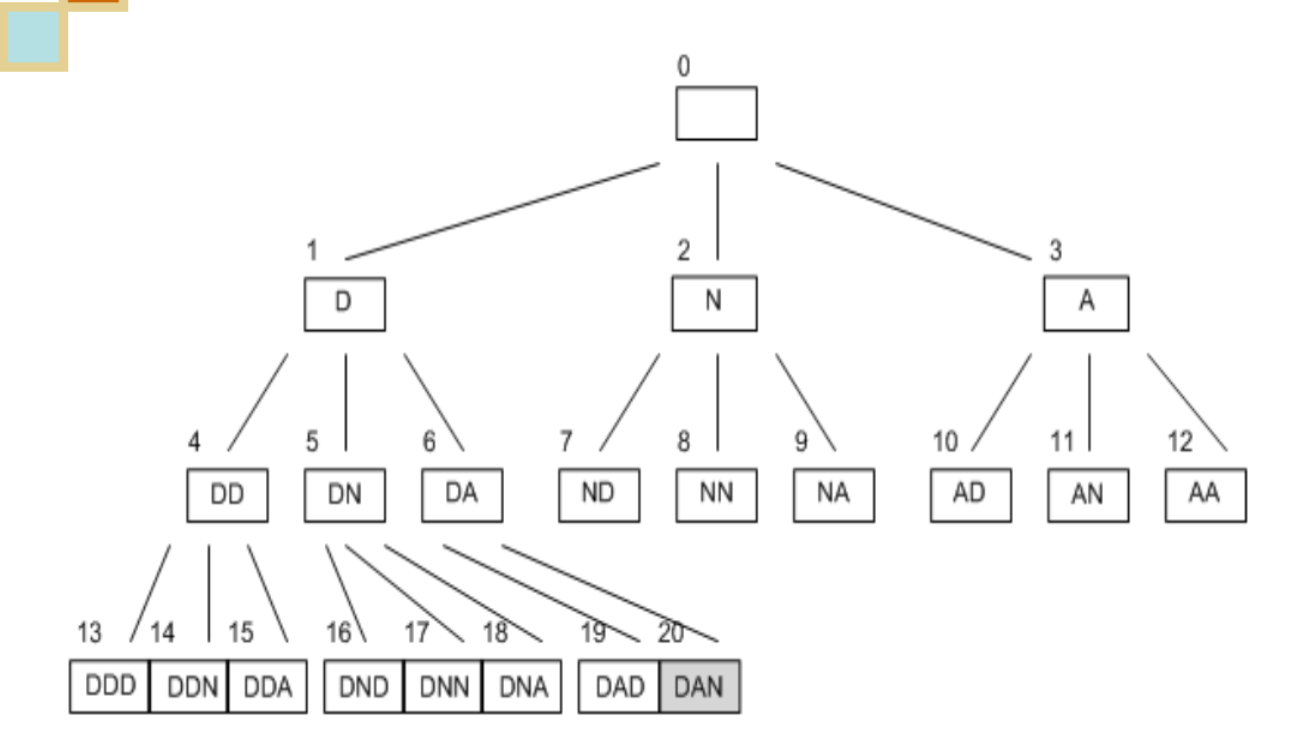
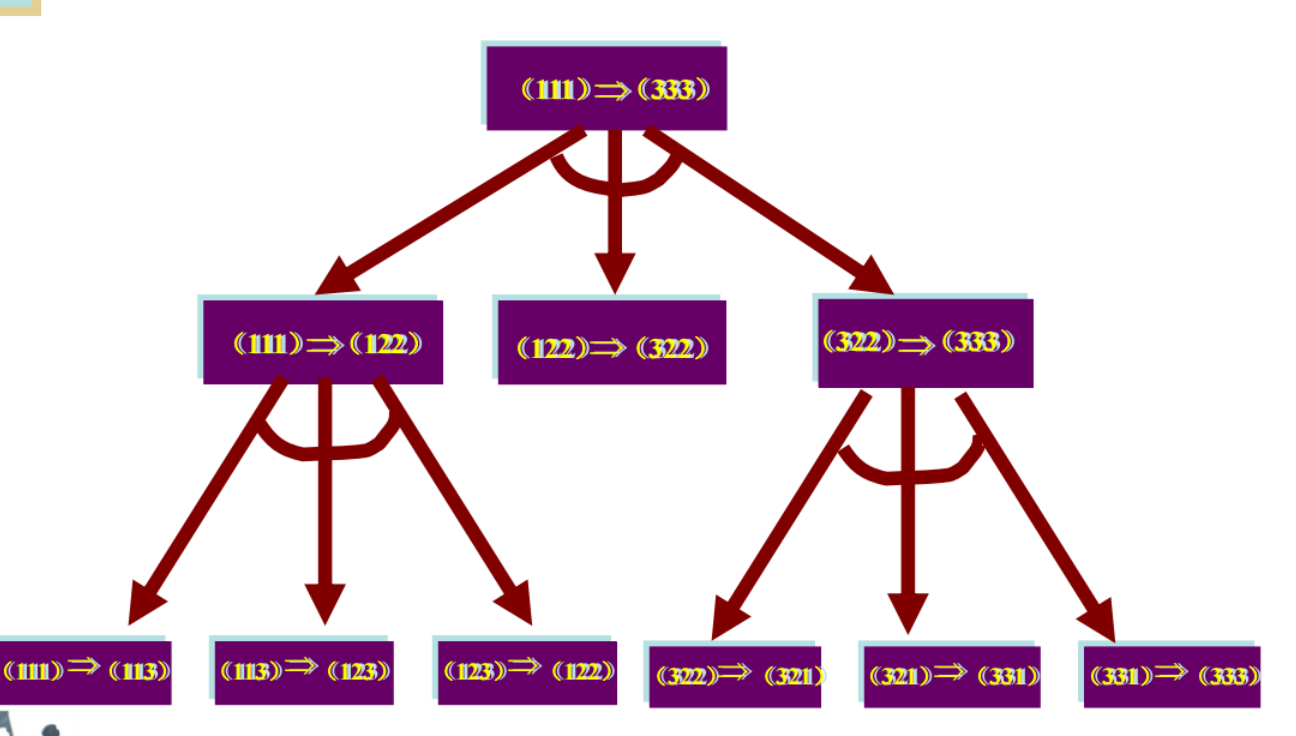
1.3.2 A name of a boy
Genetics Professor
Wanting to name her new baby boy
Using only the letters D,N & A
Search by writing down possibilities (states)
D,DN,DNNA,NA,AND,DNAN, etc.
Operators: add letters on to the end of already known states
(i) add a ‘D’ to an existing string
(ii) add an ‘N’ to an existing string and
(iii) add an ‘A’ to an existing string
Initial state is an empty string
Goal test
Look up state in a book of boys names
Good solution: DAN
Question
How many strings of 3 or fewer letters are there where the
letters are D, N or A?
Are you guaranteed to find all boys names with letters D,
N and A in this manner?
Answer
For strings of length 3, there are three choices for the first
letter (D, N and A), three choices for the second and three
choices for the third. Hence, there are 333 = 27 possible
three-letter names with D, N and A in. Similarly, there are
3*3 = 9 possible two-letter names and 3 possible one
letter names. Adding all the possibilities up, we get: 27 +
9 + 3 = 39 possible names.
Yes, all names will eventually be enumerated .
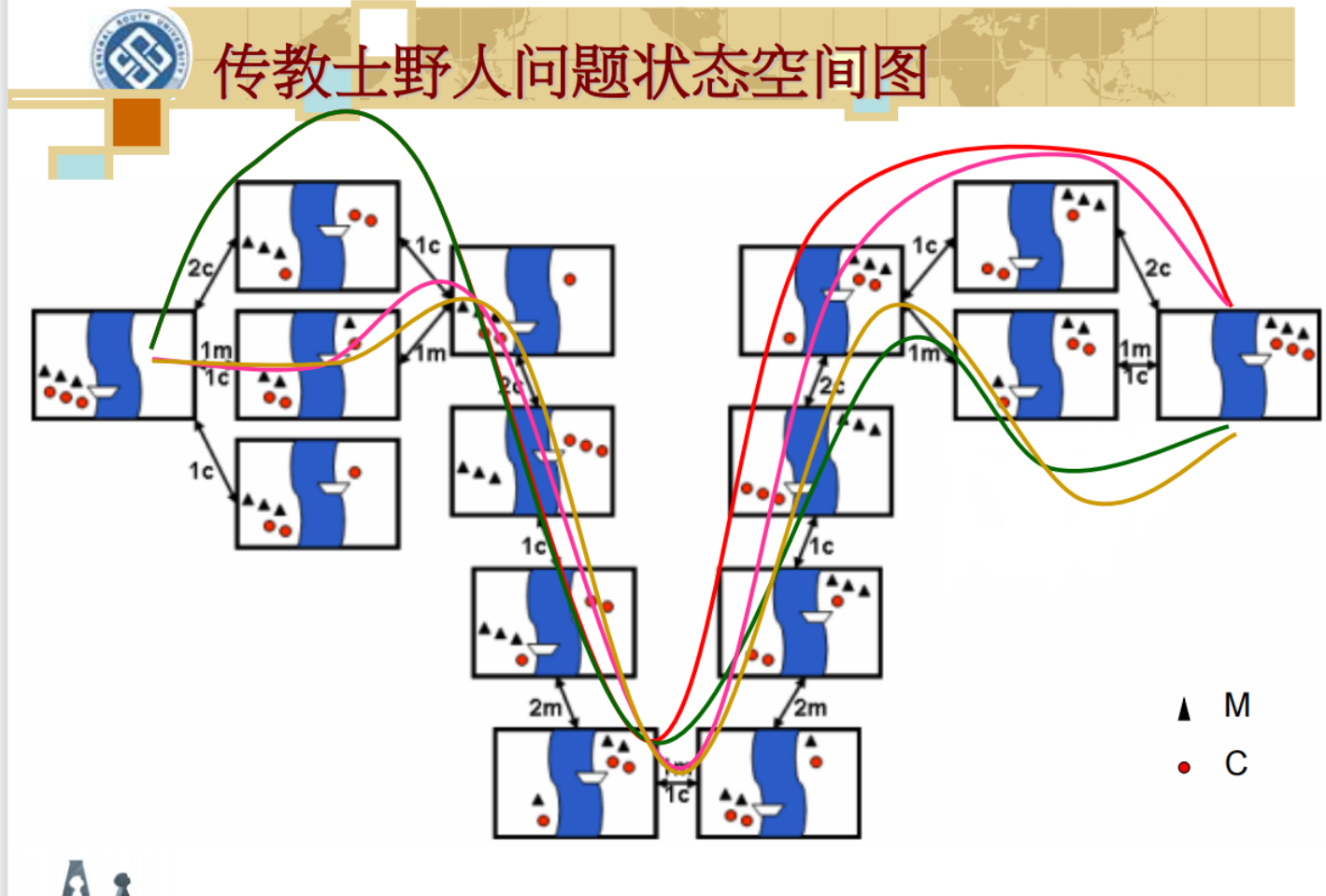
1.3.3 传教士与野人问题
有三个传教士M和三个野人C过河,只有一条能装下两个人的船,在河的一方或者船上,如果野人的人数大于传教士的人数,那么传教士就会有危险,你能不能提出一种安全的渡河方法呢?
如何定义状态?
有意义的状态共有多少种?
有哪些可进行的操作,操作的执行条件和动作是
怎样的?
状态:问题在某一时刻所处的“位置”,“情况”等
根据问题所关心的因素,一般用向量形式表示,每一位表示一个因素


二、问题归约法
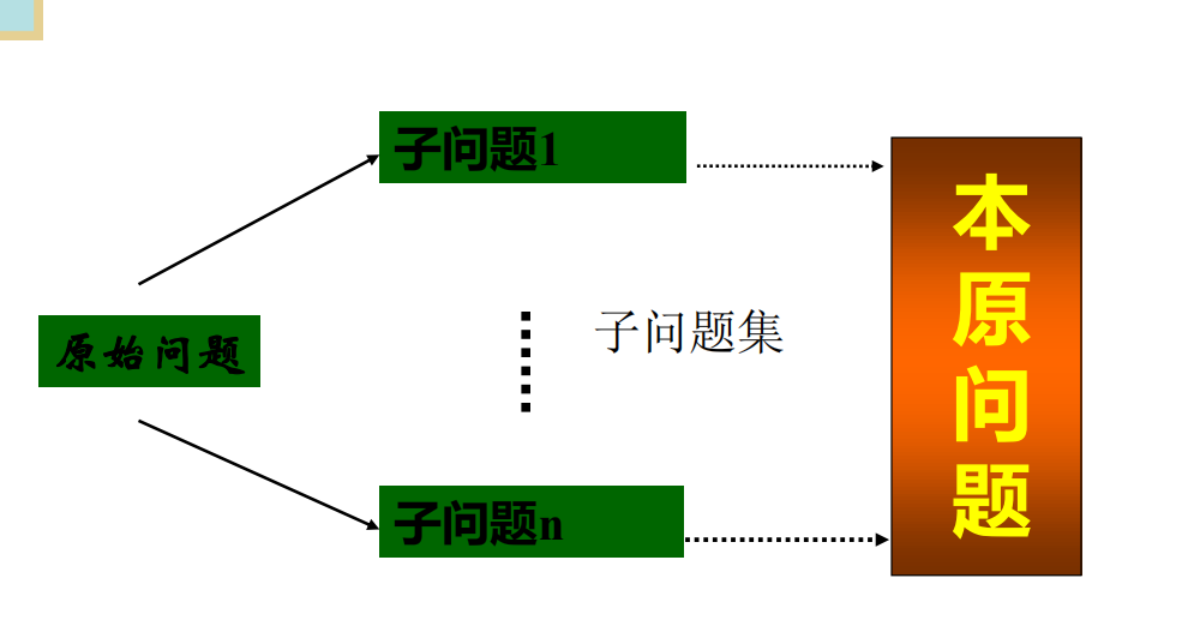
问题归约表示的组成部分:
一个初始问题描述;
一套把问题变换为子问题的操作符;
一套本原问题描述。
问题归约的实质:
从目标(要解决的问题)出发逆向推理,建立子问题以及子问题的子问题,直至最后把初始问题归约为一个平凡的本原问题集合。
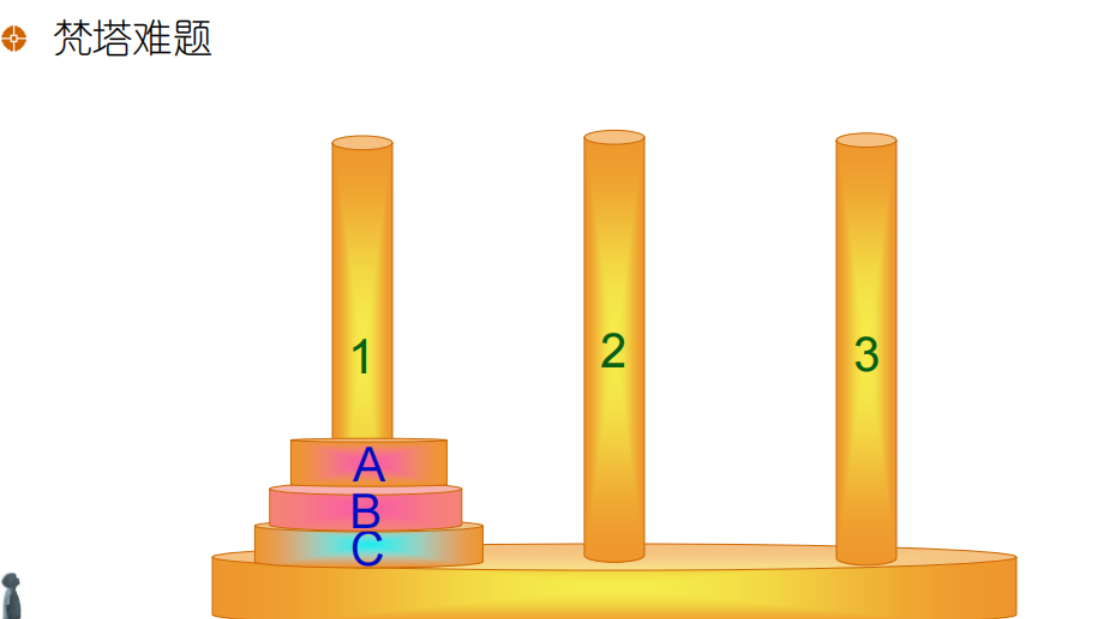
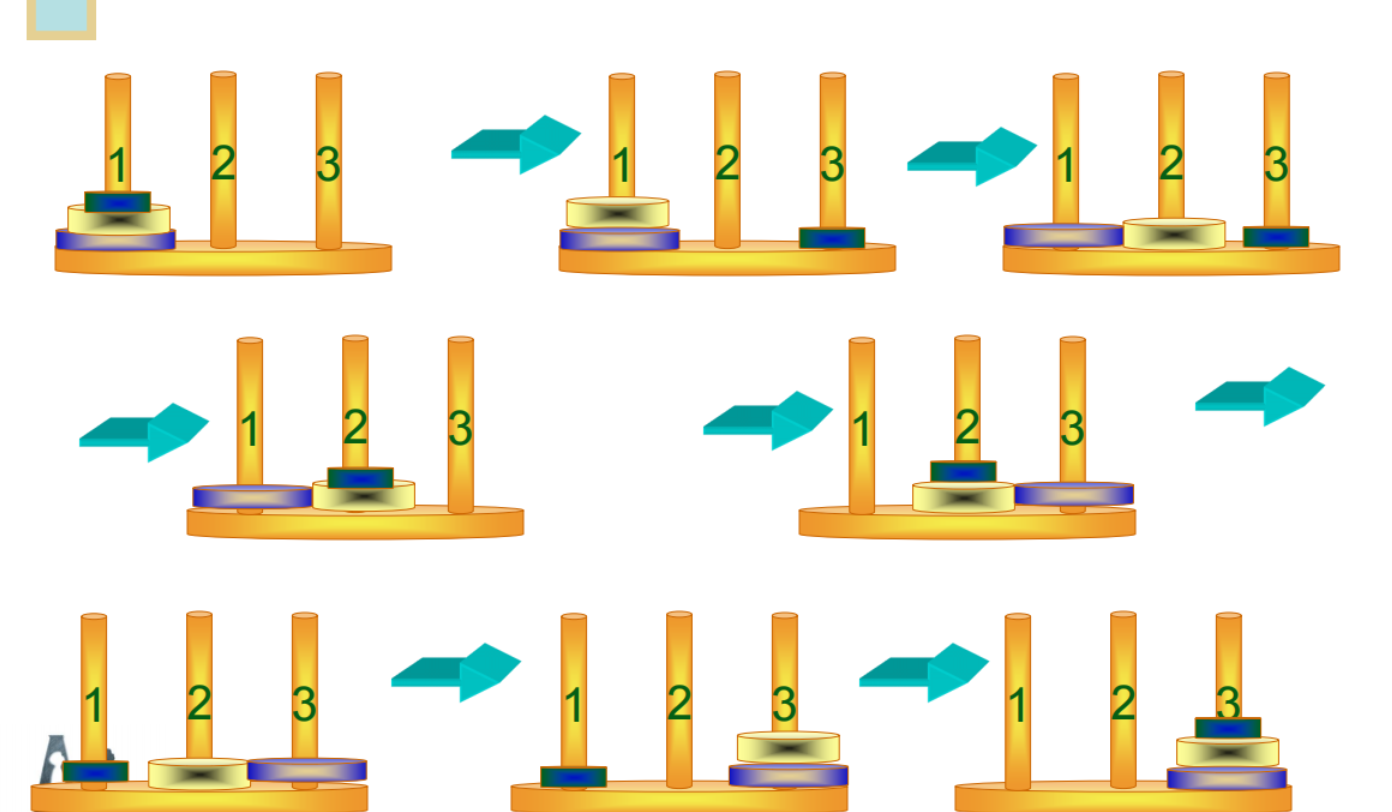
2.1 梵塔问题
2.2 与或图
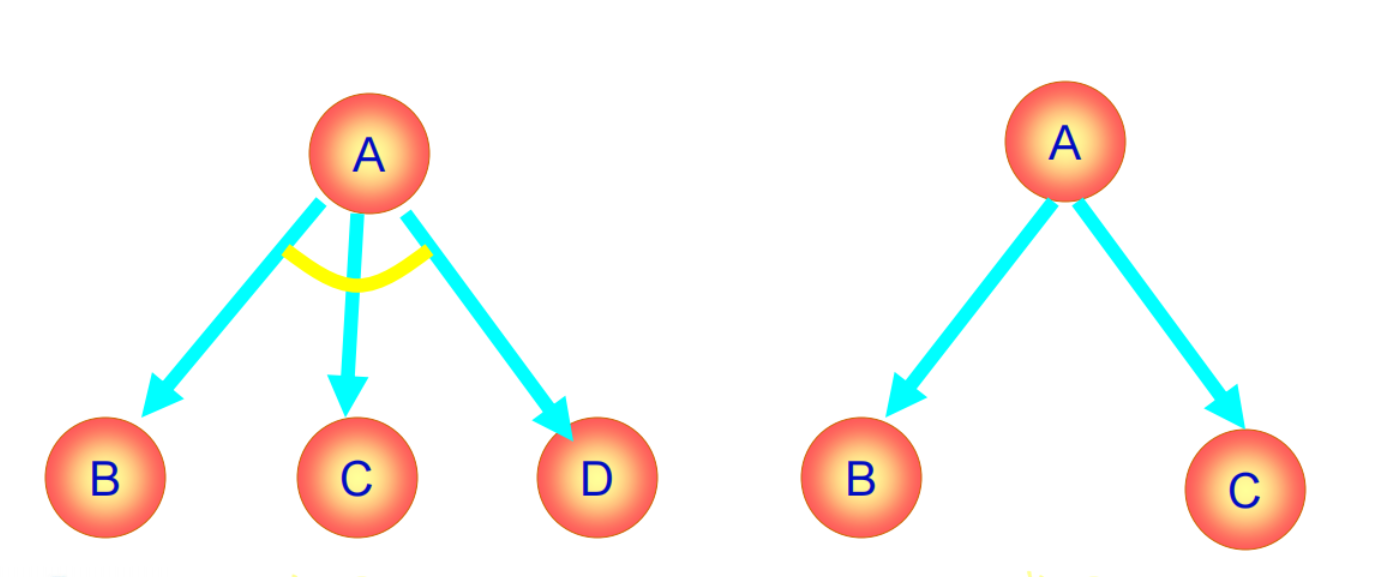
2.2.1 与图、或图、与或图
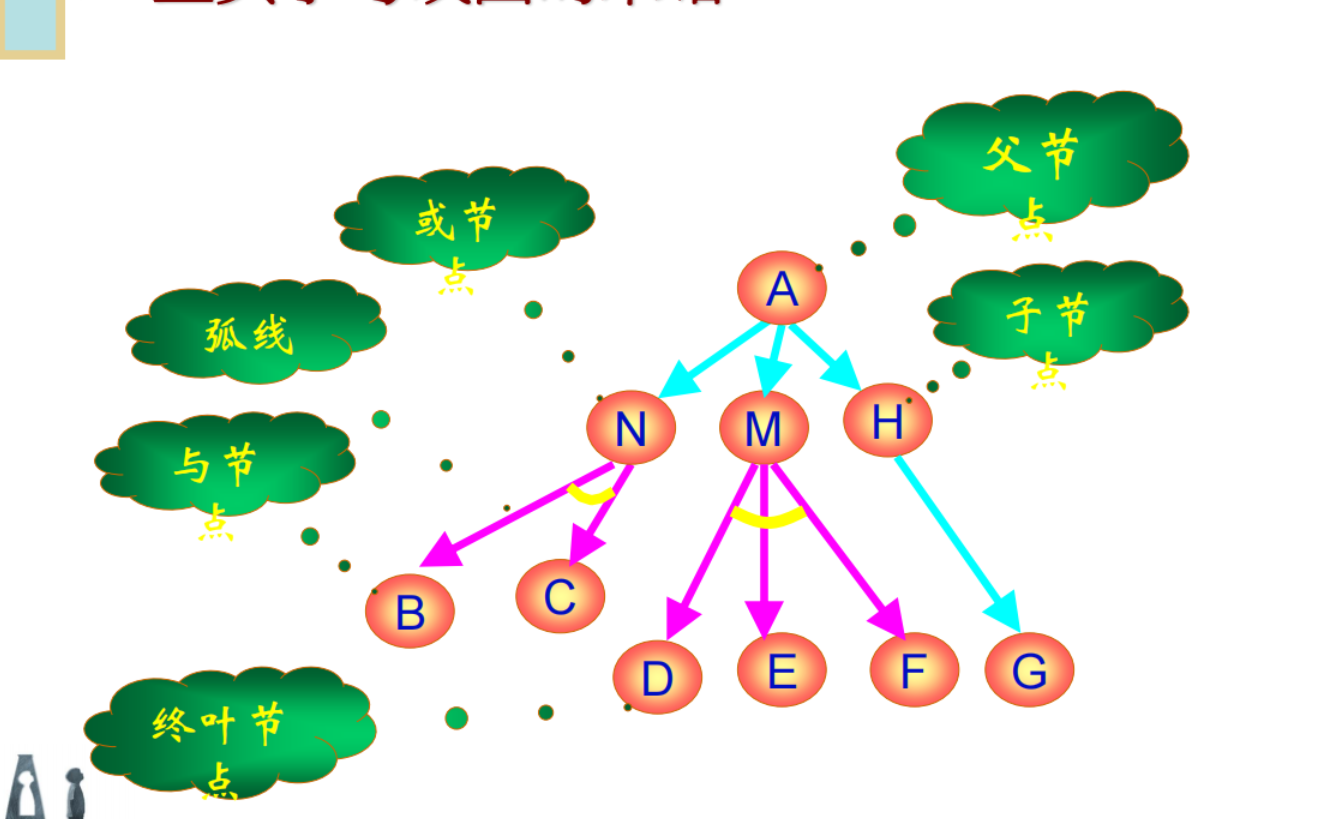
不可解节点的一般定义
- 没有后裔的非终叶节点为不可解节点。
- 全部后裔为不可解的非终叶节点且含有或后继节点,
- 此非终叶节点才是不可解的。
- 后裔至少有一个为不可解的非终叶节点且含有与后继节点,此非终叶节点才是不可解的。
与或图构成规则
- 每个节点对应一个问题或一个问题集合
- 终叶节点对应一个本原问题
- 通过算子将问题转化为子问题集合
- 通过连接线将同一个子问题的“与”节点连接起来
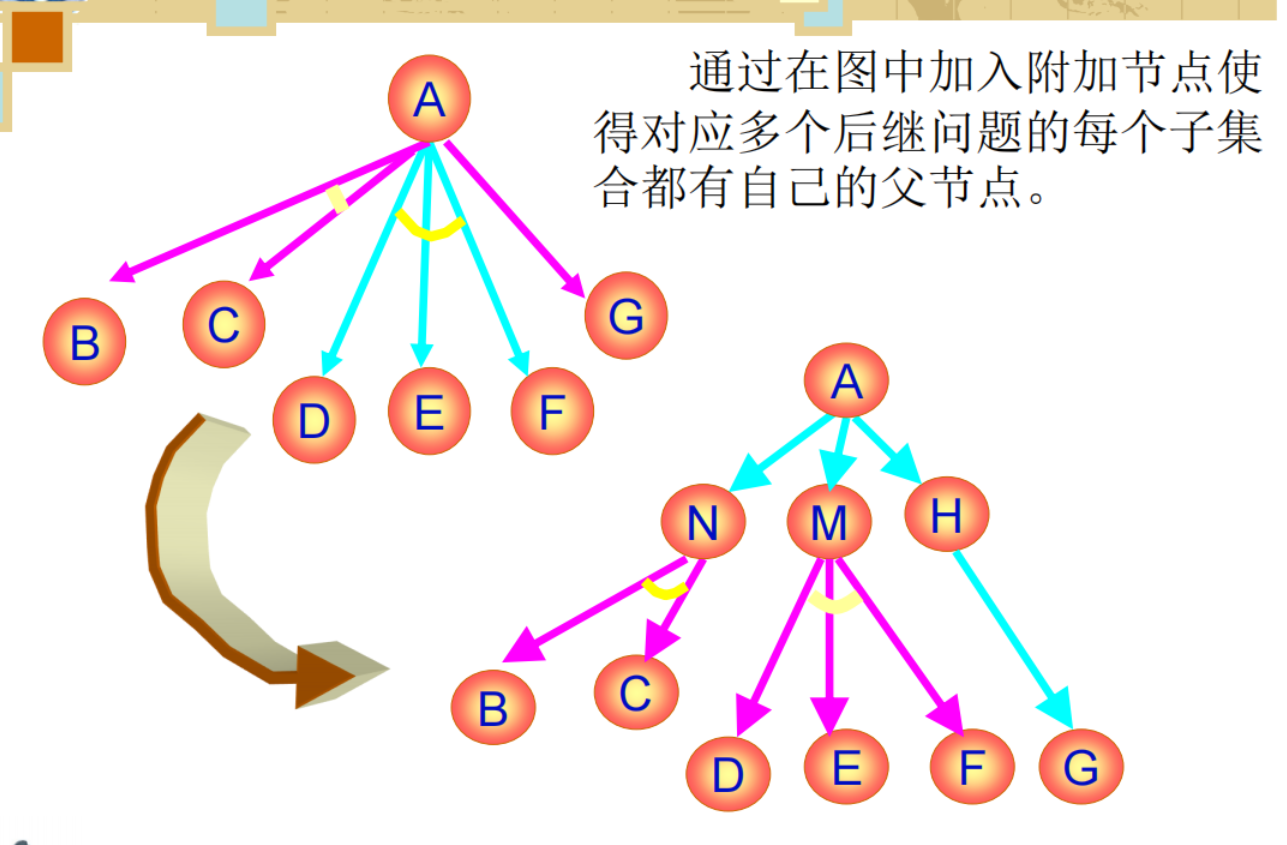
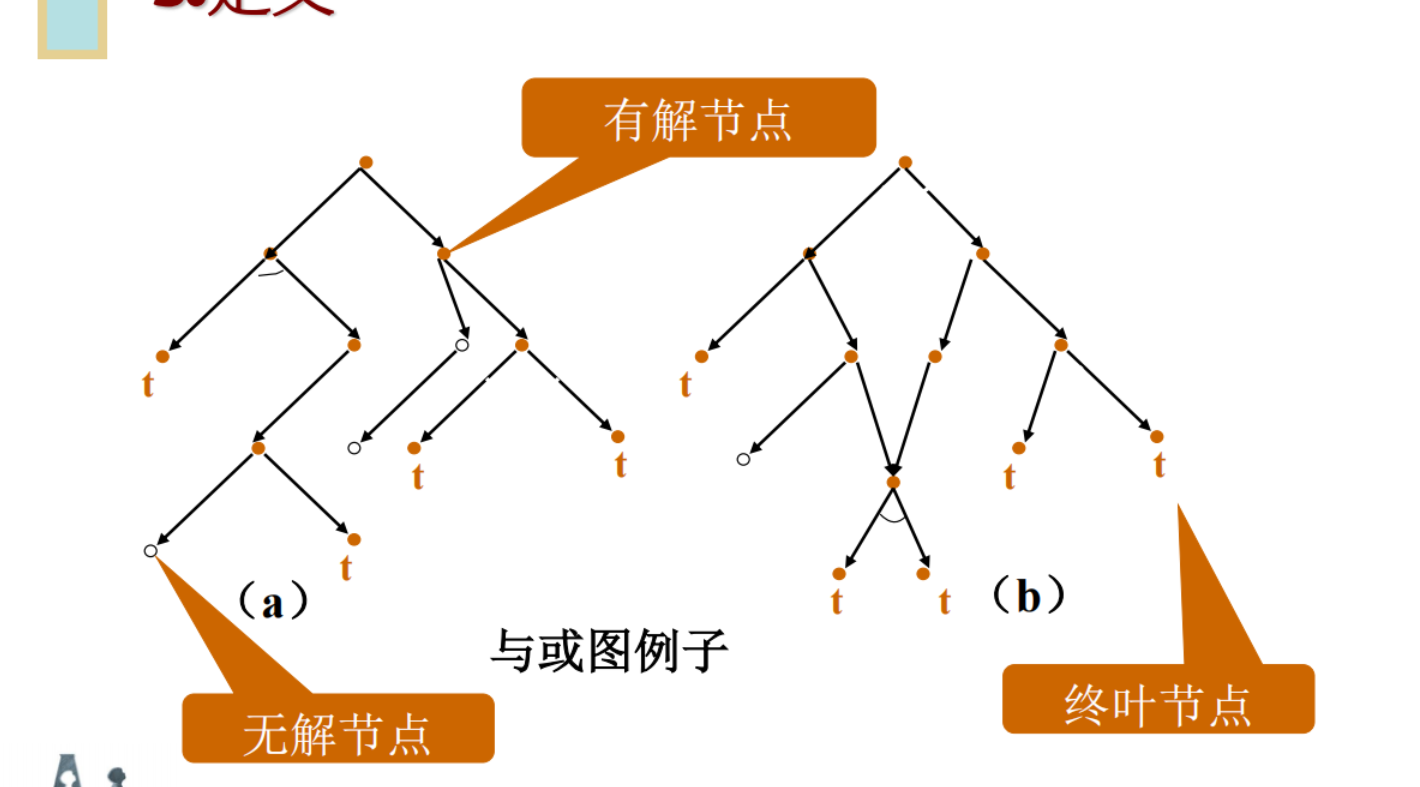
2.3 步骤:
- 与或图中的每个节点代表一个要解决的单一问题或问题集合,起始节点对应原始问题;
- 对应于本原问题的节点,叫做终叶节点,它没有后裔;
- 把问题变换为一个子问题集合,用有向弧线指向后续节点;
- 把据有共同父节点的与节点后裔的所有弧线用小弧线连接起来;
- 当只有一个算符应用于问题,代表子问题集合的中间或节点可以省。
答案:
三、谓词逻辑法
什么是谓词?
原子命题中刻画个体的性质或个体间关系的成分
- 谓词逻辑是一种形式语言
- 是目前为止能够表达人类思维活动规律的一种最精确的语言
- 接近自然语言,又方便存入计算机处理
- 最早应用于人工智能中表示知识
- 适合于表示事物的状态、属性、概念等,也可用来表示事物间确定的因果关系
3.1 谓词公式
Terms(项)
a. 一个常量是项
b. 一个变量是项
c. 如果f是一个n元函数符号,t1,t2,…,tn是项,则f(t1,t2,…,tn)也是项
d. 所有项都是由规则(a)(b)©产生的
Atoms(原子公式 )
如果P是一个n元谓词符号,t1,t2,…,tn是项,则P(t1,t2,…,tn) 是一个原子公式或原子谓词公式,其他任何表达式都不是原子公式.
当对应的语句在定义域内为真时值为真T,否则为假F.



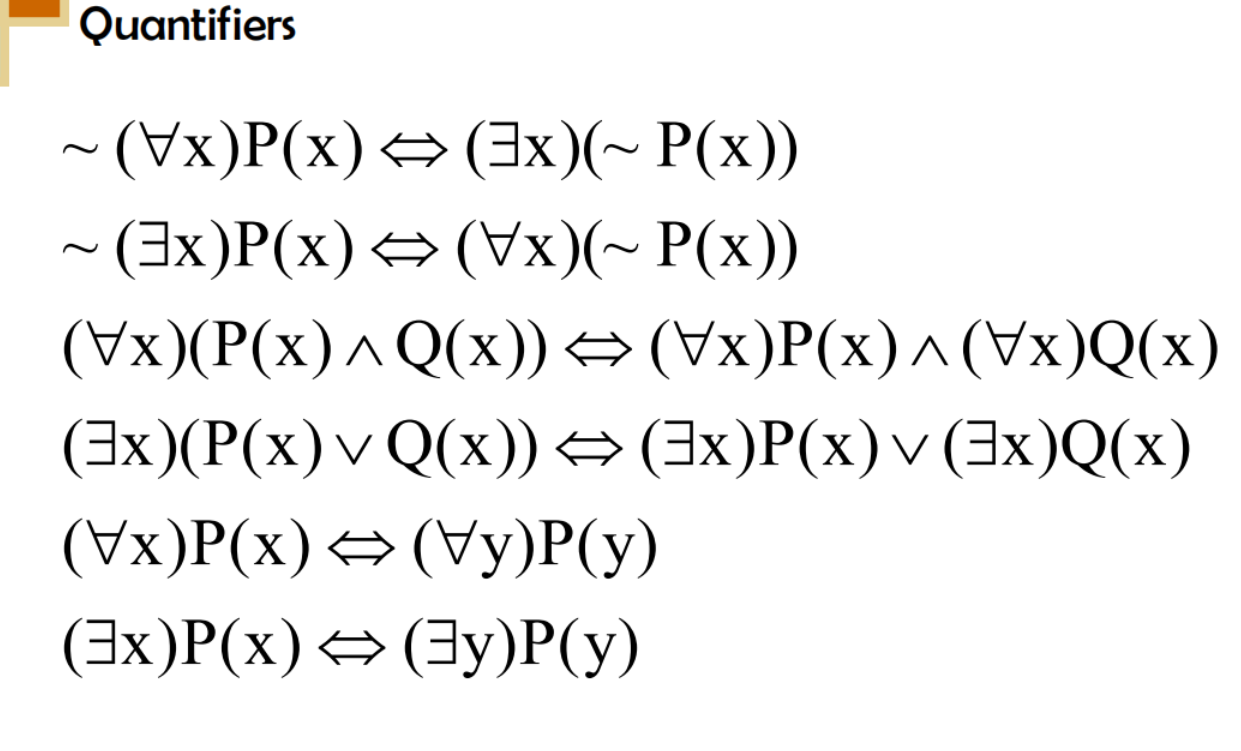




例题