一、最大类间方差遗传算法

最大类间方差的求解过程，就是在解空间中查找到一个最优的解，使得其方差最大，而遗传算法能非线性快速查找最优解k*及最大的方差，其步骤如下：
①为了使用遗传算法，首先必须对实现解空间的数值编码，产生染色体单元。由于所采集到的道路图像的灰度图由0~255个灰度值组成，正好对应着一个8位二进制即一个字节，因此使用一个字节作为一个染色体。对于染色体的解码正好是编码的逆过程，就是这个字节的十进制数。
②初使化种群，产生一个规模的染色体种群，并随机初始化每一染色体，得到多个不同的染色体，这个过程实际上决定了解的起始值，如果其选取过偏，则会造成最优解收敛慢、计算时间长的缺点。
③对每个染色体进行解码。由最大类方差的分割阈值方法，可以设定其方差作为每一个染色体的评价函数，染色体的方差越大，就越有可能逼近最优解。求出每一个染色体的适应值，对于所求得的适应值，求出每一个染色体的选择概率及累计概率并产生多个随机数。选择出随机概率对应的染色体作为遗传运算的一组种子，其中适应值大的被选取的可能性大，而适应值小的被选取的机会少，其值对染色体进行优胜劣汰的自然选择，又称为竞争。被选中的染色体作为遗传种子，进行遗传运算，这样一代一代地进行，每一代所得到的适应值都不相同，新一代中的染色体得到的适应值较高，因此，其解也更逼近于最大的值。
④接下来进行遗传运算。首先进行杂交运算，杂交运算就是对染色体中的某些基因进行交换，此过程中为了控制交换的位数，必须给定一个杂交率。杂交率越大，其交换的基因越多，其值变化就越快，解的收敛速度就越快；但杂交率太大，不利于求得最优解。

二、代码示例

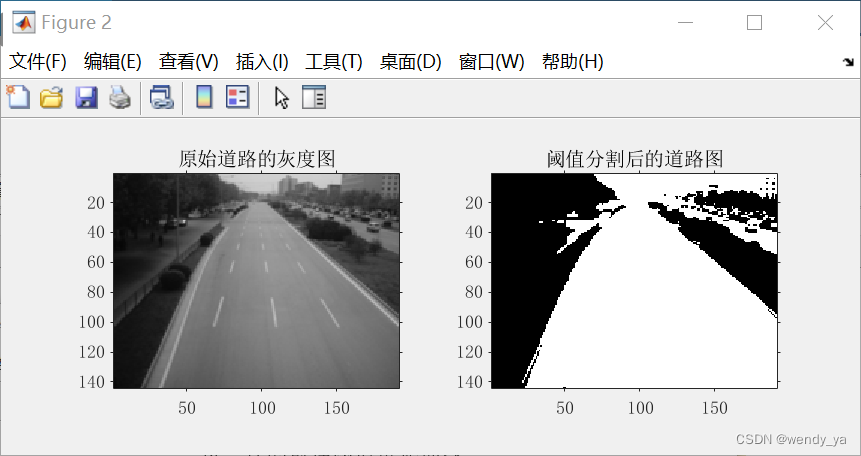
运用最大类间方差遗传算法进行道路分割的MATLAB代码和效果如下：
原始道路和分割后的道路图像如下：

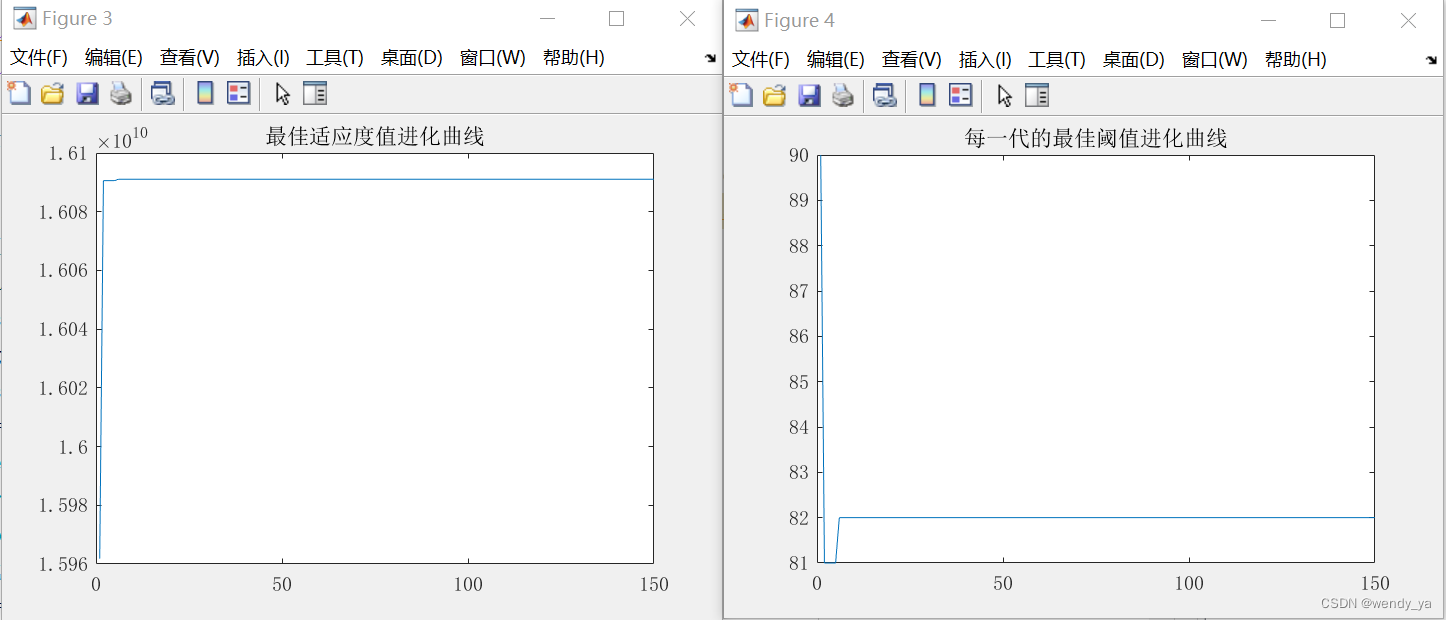
最佳适应度值进化曲线和每一代的最佳阈值进化曲线如下：

【注】：将传统的图像分割技术与现代智能理论——遗传算法相结合，不但提高了算法的分割性能，还大大提高了算法的运算速度。
完整代码参考链接：https://download.csdn.net/download/didi_ya/87691646