作者:小迅
链接:https://leetcode.cn/problems/steps-to-make-array-non-decreasing/solutions/2213056/dan-diao-zhan-zhu-shi-chao-ji-xiang-xi-b-rvv0/来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
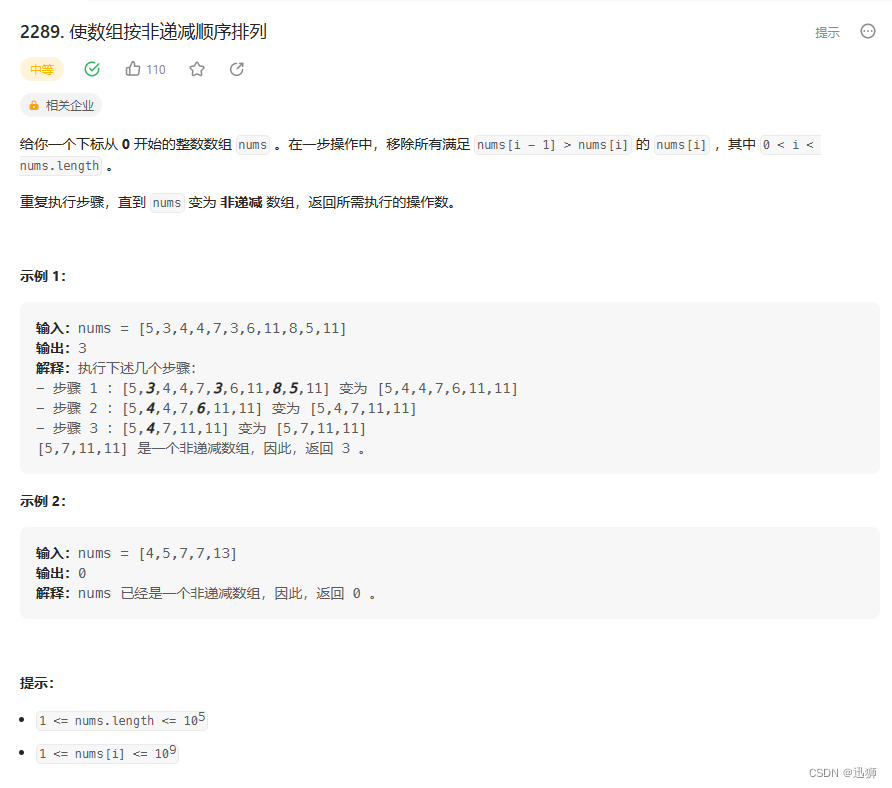
题目
思路
题意 -> 给定一个数组返回使得数组单独递增的最少操作数
- 一次有效操作为:移除所有满足 nums[i - 1] > nums[i] 的 nums[i]
对于数组单调性题目,单调栈都是一个不错的辅助数据结构。
单调栈
- 思路:
- 每个元素一定时被左侧第一个更大的元素消除的
- 设 x 消除 y,也就是 [x] .... [y],那么 中间的 .... 一定先被消除,再 +1 次消除(x 消除 y)
- 那么,x 被消除所需轮数就是 [....] 中的最大消除轮数 + 1
- 具体实现:
- 对应两个数组,一个用作 栈 - 保存左边第一个最大值下班,一个用于保存第 i 个数在第几次被移除。枚举所有元素,记录每一个元素的移除顺序,返回最大移除数。
代码注释超级详细
代码
int totalSteps(int* nums, int numsSize){int res = 0;int s[100001] = { 0 }; // 用单调栈存下标,用来找左边第一个大值int dp[100001] = { 0 }; // dp[i]: 第 i 个数在第dp[i]次被移除int top = 0;for (int i = 0; i < numsSize; ++i) { //枚举每一个元素 int cur = 0;while (top > 0 && nums[s[top - 1]] <= nums[i]) {//选择最近最大值cur = fmax(cur, dp[s[top - 1]]);//记录最大消除数top--;}if (top > 0) {//如果单调栈中有数据,那肯定比自己大,当前元素肯定会被移除,+1表示自己移除dp[i] = cur + 1;res = fmax(res, dp[i]);//保存最大数}s[top++] = i;}return res;
}作者:小迅
链接:https://leetcode.cn/problems/steps-to-make-array-non-decreasing/solutions/2213056/dan-diao-zhan-zhu-shi-chao-ji-xiang-xi-b-rvv0/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。