搜索二叉树
- 搜索二叉树的定义
- 插入
- 查找
- 遍历
- 删除(重点)
- 总结
前言:文章中的代码大多以截图的形式呈现,文章的结尾处有二叉搜索树的代码链接。
搜索二叉树的定义
搜素二叉树:
若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。
如下图所示:
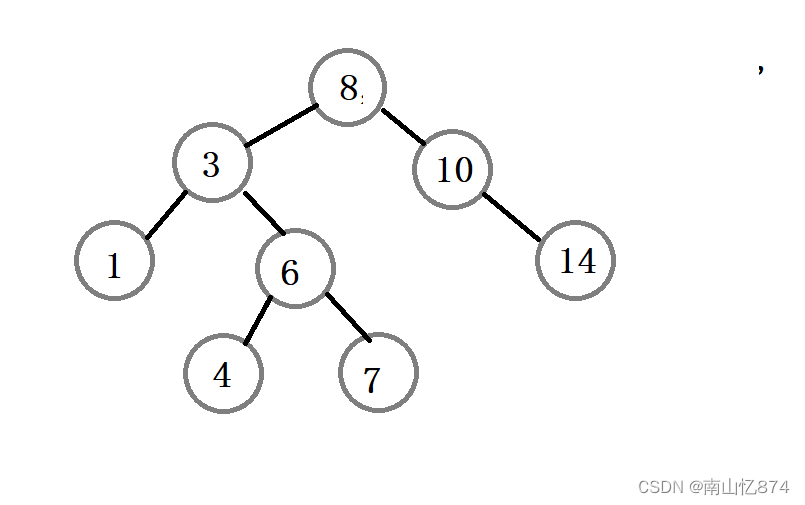
所以在写代码的时候我们需要一个结点的结构体,结构体的内部要有两个指针(left和right)和一个值。
那么我们先将基本的准备工作做好之后就开始实现有关二叉树搜素树的各种接口。
准备:
template<class K>struct TreeNode{TreeNode<K>* _left = nullptr;TreeNode<K>* _right = nullptr;K _key;TreeNode(K val):_key(val){}};template<class K>class BSTree{typedef TreeNode<K> node;public://接口。。。node* _root = nullptr;};
插入
根据二叉树的特点,比根大的在右边,比根小的在左边。那么我们在插入的时候只需要用if语句进行简单的判断就可以确定插入结点的位置,额外需要我们考虑的之有,当我们插入的是第一个结点时,这个结点就是根结点。
现在以上图为例,假设我们要插入的是16。那么16的位置应该在下图所示的位置。
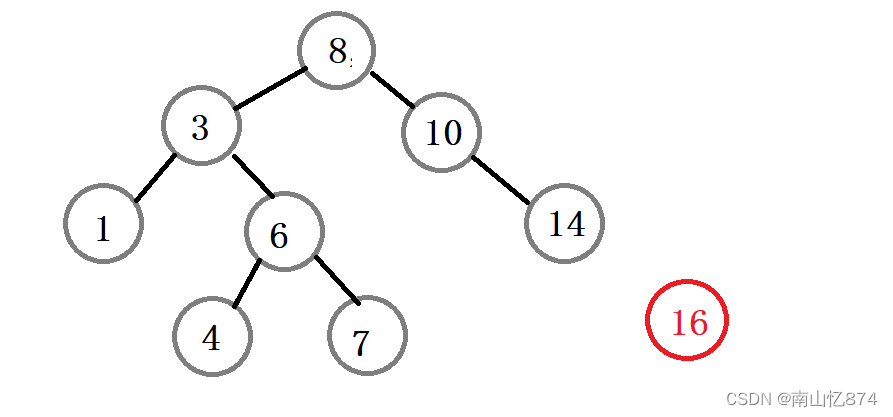
我们找到了16的正确插入位置之后,下一步该考虑的就是如果让14和16建立链接?
如果我们只许使用一个结点去找插入的位置,就无法将插入的结点和它的”父节点“建立链接,因此我们还需要一个结点来帮助我们找到插入位置的父结点是谁!
所以我们的代码相当于需要两个指针,一个指针用来找插入结点的正确位置,一个指针用来记录上个指针的前一个结点,我们分别用cur 和parent命名两个指针。
那么插入的代码就如下所示:

最后需要注意的就是代码的最后一部分,当我们的parent和cur都来到了正确的位置之后,我们还需要判断一下cur是parent的左节点还是右节点。
这一点在下面最复杂的删除的时候,也会用到,之后便不再解释,望熟知!!!
查找
插入的代码看懂了之后,查找应该就不用我说了。
遍历
根据搜索二叉树的特点,我们结合中序遍历,出来的结果就是有序的了,并且在STL中的set底层二叉搜索树的遍历方式也是中序遍历。
遍历我们使用递归实现。
需要一提的是我们是使用的private修饰的根节点,所示对象是无法直接进行调用的,这个时候我们的递归就无法进行下去,那么解决办法有两个(通常不会去修改private):
一:在类中在定义一个getroot函数,帮助我们拿到对象的根节点,我们在进行递归的时候,调用这个函数即可。
二:
再封装一层函数:如下图所示:


我们使用InOrder去调用_InOrder就能解决。
关于中序遍历的思路这里就不再进行过多的介绍了。
后续我们在实现各种接口的递归版本的时候,也是查用此方式解决,望熟知!!
删除(重点)
搜索二叉树最难的部分就是删除,特别是在用循环实现的时候,特别的情况需要大家有一定的清晰的认识。
要删除某个结点,第一件事肯定还是要找到该结点,如果该结点就返回false,在我们找到之后就要开始删除。查找的思路和find是一样的。
第一种情况:
现在还是以上图为例,假设我们要删除的是结点14。
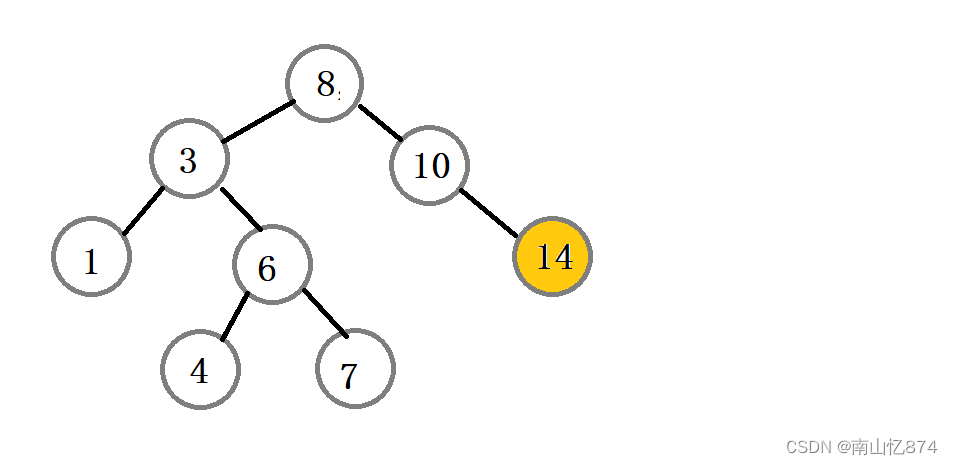
14的左右子树都为空,这时我们只需要将10的右指向改为空,再释放掉14结点即可。
所以不难看出,我们还是需要俩个指针,作用和插入的时候一样。!!!
第二种情况:
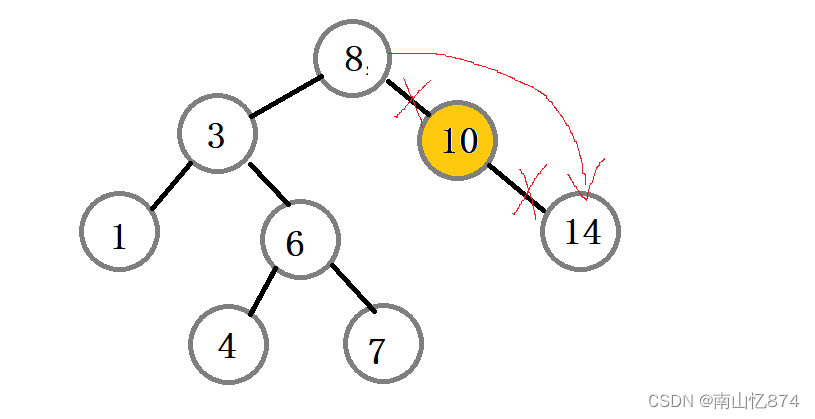
假设我们要删除的结点是10,此时10的左子树为空,右子树不为空。
我们只需要将8的左指向改为10的右子树,再释放掉10结点即可。
示意图如下:
再来看第三种情况:
为了构造出第三种情况,我们将图改一下,然后我们要删除的是6这个结点:
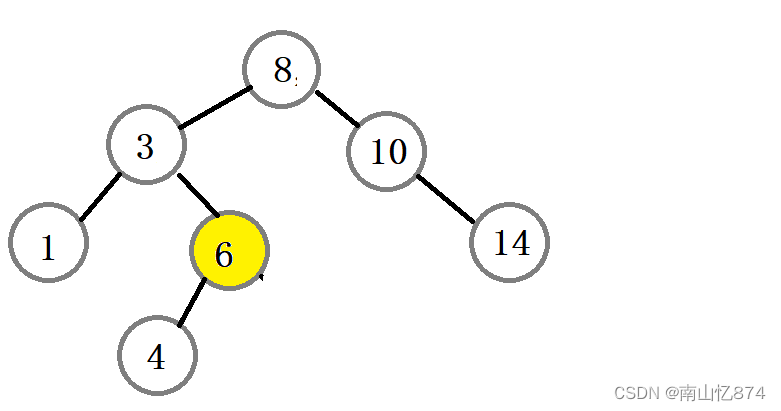
此时的6结点的右子树为空,我们只需要将它的父节点3的左指向改为6的左指向,再释放掉6结点即可。
以上的三种情况都是比较简单的场景,接下来还有一种最为复杂的情况我们等会再看,现在将上述的三种情况进行一下总结:
我们仔细一点便会发现,其实可以将第一种情况省略或者说归到第二或第三种情况当中去。
那么也就是我们要先处理一下两种情况
一,要删除的结点的左子树为空
二,要删除的结点的右子树为空
删除的步骤就是,先建立新链接,再释放结点。
代码如下:
bool Erase(const K& key){node* parent = nullptr;node* cur = _root;while (cur){//先找到要删除的结点if (cur->_key < key) {parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{//找到了,开始删除//1.该结点的左子树为空//2.该结点的右子树为空//3.左右都不为空--最复杂的情况if (cur->_left == nullptr){//还需要进一步的判断一下cur是父节点的那个字树if (parent->_left == cur)parent->_left = cur->_right;elseparent->_right = cur->_right;delete cur;}else if(cur->_right == nullptr){if (parent->_left == cur)parent->_left = cur->_left;elseparent->_right = cur->_left;delete cur;}else{//左右子树都不为空的情况//替换法删除--找右子树的最小结点(√) / 找左子树的最大结点都是可以的//。。。。。}return true;//删除成功}}//没找到/树为空return false;}
现在关于前两种情况的删除就完成了,再谈第三种删除场景时,我们还需要考虑一种极端的情况。
加入有下图一个搜索二叉树,左子树为空,且我们要删除的结点是8
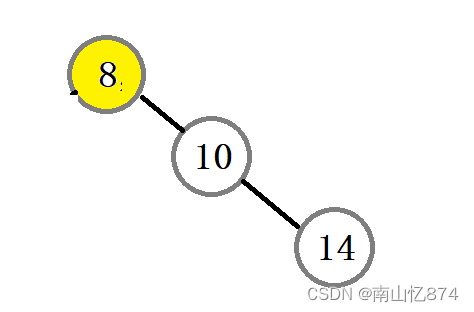
如果按照我们上面所述的代码进行删除的话,不难发现,根本走不通,当cur来到8的位置的时候,parent还是一个空指针,这时上述的代码就会出现崩溃的情况。
面对这种情况的时候我们要进行额外的处理。
处理的方式也很简单,只需要将cur直接走到10,再释放根节点即可。
所以我们就需要在上述的代码中加入一个if判断来处理这种极端情况,代码如下:
//找到了,开始删除//1.该结点的左子树为空//2.该结点的右子树为空//3.左右都不为空--最复杂的情况if (cur->_left == nullptr){//极端情况if (cur == _root){_root = cur->_right;}else{//还需要进一步的判断一下cur是父节点的那个字树if (parent->_left == cur)parent->_left = cur->_right;elseparent->_right = cur->_right;}//断开链接之后还需要释放掉结点delete cur;}else if(cur->_right == nullptr){//右子树为空也一样。if (cur == _root){_root = cur->_left;}else{//与上同理if (parent->_left == cur)parent->_left = cur->_left;elseparent->_right = cur->_left;}delete cur;}else{//左右子树都不为空的情况//替换法删除--找右子树的最小结点(√) / 找左子树的最大结点都是可以的//。。。。。}
这时,除了第三种情况以外,我们的代码就都能进行有效删除了!
如果你理解了上述的两种情况+一种极端例外之后,我们再来看第三种复杂情况:
第三种情况:
要删除的结点的左右子树都不为空!
比方说我们要删除的是下图的3结点:
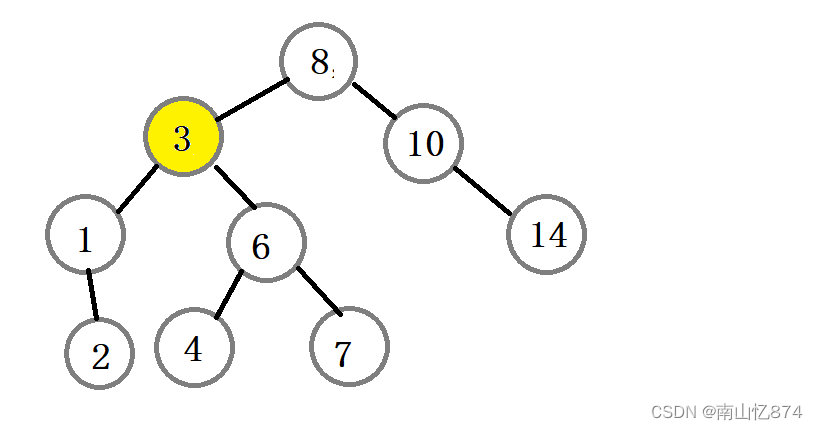
如果想要删除3的话,我们就需要有一个结点来代替3结点的位置,且该结点不破坏掉原树的搜索二叉树的结构!
要想找到这个合适的替换结点其实也很简单,还是根据搜索二叉树特性:
要么找 3 结点的左子树的最大结点或者找 3 结点的右子树的最小结点
也就是上图中的2或者4结点:
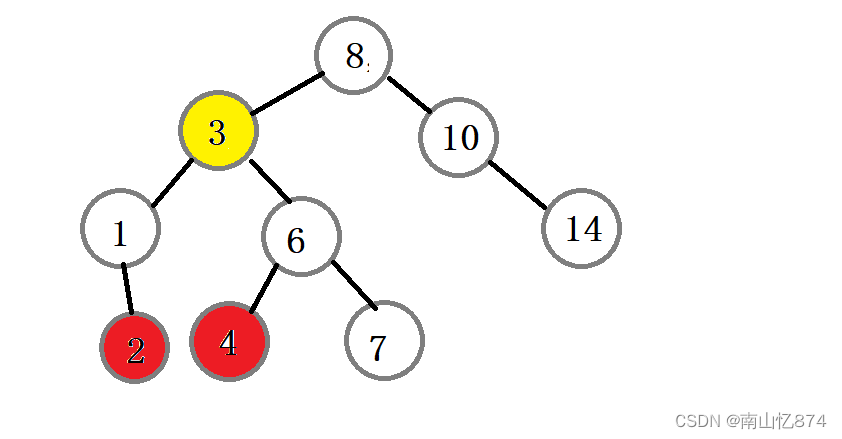
下面的实现是找3的右子树的最小结点。望熟知!
找到了要替换的结点之后,我们就要开始删除的工作:
第一步:交换结点值
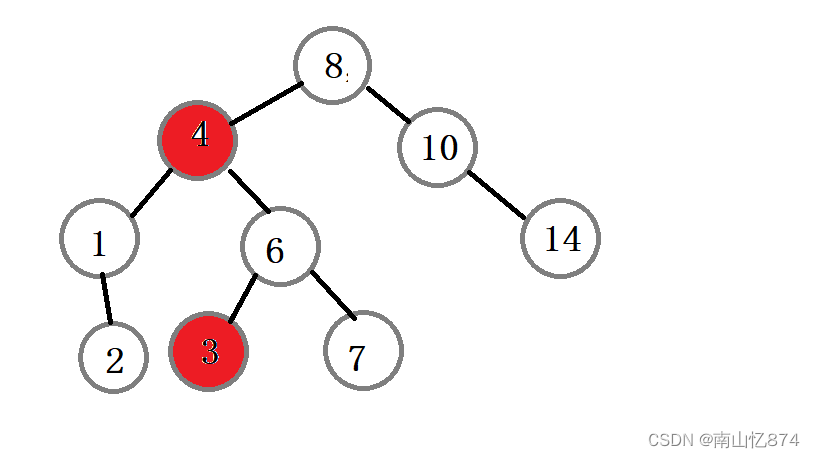
第二步:删除3结点,我们找的是右子树的最小结点,最小结点的左子树一定是为空的,那么我们只需要将6结点的左指向链接到3的右子树即可,不必关心要删除的结点的右子树是否为空示意图如下:
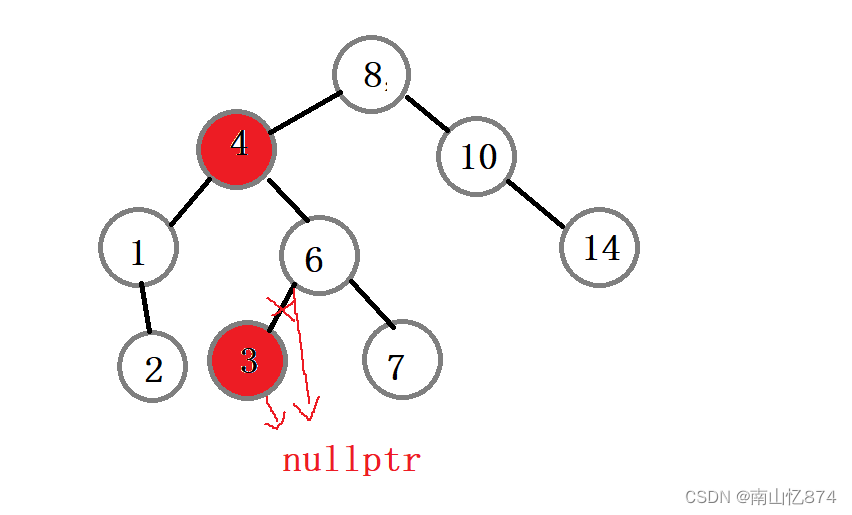
第三步:释放3结点
至此我们第三种情况的删除就完成了,代码如下:
//左右子树都不为空的情况//替换法删除--找右子树的最小结点(√) / 找左子树的最大结点都是可以的node* min = cur->_right;node* minparent = nullptr;//删除根节点while (min->_left){minparent = min;min = min->_left;}swap(cur->_key, min->_key);minparent->_left = min->_right;delete min;
不过删除还没有结束,因为我们上述的代码还是处理不了另外一种极端的情况
假如我们要删除的是根节点8呢???
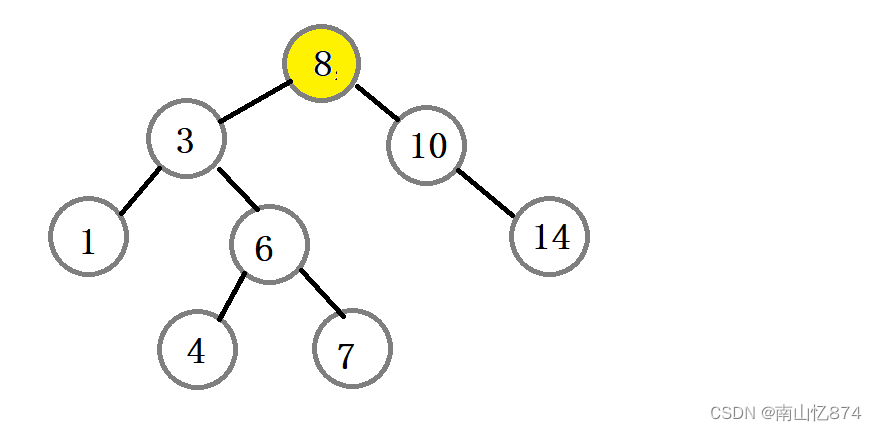
此时8的左右都不为空,属于我们的第三种情况,但是如果我们按照上述的代码进行删除的话,会发现和插入时一样的问题,parent为空!!!
难道我们还要进行一次特殊的处理吗?
并不用,处理这种情况,我们只需要将patent的初始值改为cur即可,如下图:
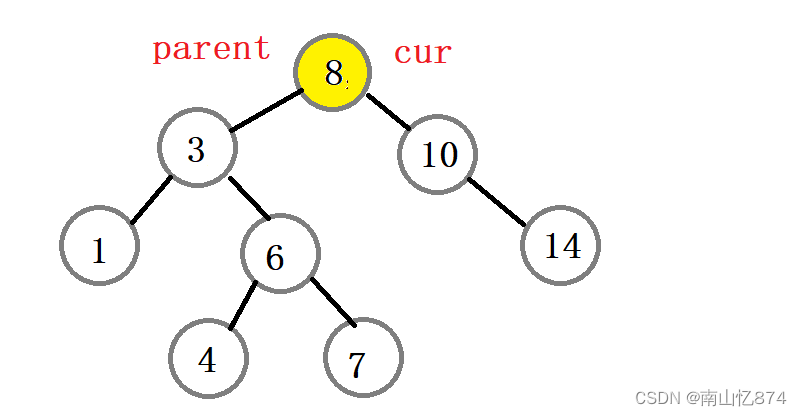
这时我们的min会找到8的右子树的最小结点,也就是10。这时再进行删除的步骤就不会出错了。
修改后的代码如下图:

总结
关于搜索二叉树的各种接口的实现,唯一的难点可能就是删除的实现,我们谈到了有三种情况+两种极端的场景。
把这部分理清晰之后,关于搜索二叉树的实现,你就算掌握的了。
代码的链接如下,其中包含了递归实现各种接口的代码,后期有时间的话我会再出一篇文章来介绍,如果有不理解的地方,欢迎交流。
二叉搜索树代码链接