brief

在生物统计学中有对应的纯理论部分，这里也有部分理论知识可以稍微了解一下。

术语速成部分

单因素组间方差分析

在这里插入图片描述

单因素组内分析

在这里插入图片描述

双因素混合模型

在这里插入图片描述

协方差分析和多元方差分析

在这里插入图片描述

R中的aov函数

在这里插入图片描述

需要注意的是car包的Anova()函数与标准anova()函数有细微区别，Anova()函数提供了类型II和类型III的选项，而anova()函数只提供了类型I的选项。

单因素方差分析

一个分类因子，将因变量分成两组或者多组，分组后的因变量均值之间的差异是否显著呢？

单因素组间方差分析

在这里插入图片描述

library(multcomp)
attach(cholesterol)
head(cholesterol)
table(cholesterol$trt)aggregate(cholesterol$response,by=list(cholesterol$trt),FUN= mean)
aggregate(cholesterol$response,by=list(cholesterol$trt),FUN= sd)fit <- aov(cholesterol$response ~ cholesterol$trt)
summary(fit)detach(cholesterol)

在这里插入图片描述
F value 以及Pr显著性检验值表明不同的治疗方法对治疗效果的作用存在显著差异，其中同一种药物不同的给药方式或者不同的药物具体那个对治疗效果存在显著性影响暂时不知。后面需要用多重比较法进行计算。

均值比较

在这里插入图片描述
两两均值比较，具体是最小显著差值法(LSD)还是最小显著极差法(LSR)好像没法指定。其中p adj 小于α=0.05认为两组均值差异显著。

par(las=2)
par(mar=c(5,8,4,2))
plot(TukeyHSD(fit))

在这里插入图片描述

或者使用multcomp包中的glht函数进行多重比较，glht既适用于线性模型也适用于广义线性模型，而且参数较丰富可以设置单尾双尾比较等。

library(multcomp)
par(mar=c(5,4,6,2))
tuk <- glht(fit, linfct=mcp(trt="Tukey")) # linfct=mcp() 设置了多重比较，即分类变量trt内部分组两两比较
plot(cld(tuk, level=.05),col="lightgrey") # cld函数设置了显著性水平
summary(tuk)

在这里插入图片描述

评估检验的假设条件

如果数据不满足方差分析的假设，结果对你有利却不一定是正确的。
单因素方差分析的因变量服从正态分布，且各组具有方差齐性。
因变量服从正态分布：自变量对应一个正态总体/因变量 = 实际值+误差，而误差呈正态分布

QQ图检验正态性假设：

library(car)
qqPlot(lm(cholesterol$response ~ cholesterol$trt, data=cholesterol),simulate=TRUE, main="Q-Q Plot", labels=FALSE)

在这里插入图片描述
残差值以理论值成45°角分布，基本满足因变量呈正态分布。

还要做分组的方差齐性检验
F检验或者巴特勒检验

bartlett.test(response ~ trt, data=cholesterol)

在这里插入图片描述

离群点检测

library(car)
outlierTest(fit)

在这里插入图片描述

单因素组内方差分析

观测对象在不同的分组下都进行了测量，比如每一个观测在多个时间点都进行了测量，比较不同时间点的均值差异显著性则为单因素组内方差分析，此时仍按照单因素组间方差分析的方法进行计算,仅仅方程式变了一点。

fit <- aov(cholesterol$response ~ cholesterol$trt+Error(cholesterol$response/cholesterol$trt))
summary(fit)

单因素协方差分析

litter数据集，包括四组变量，其中小鼠产仔重量为因变量，四组不同剂量的药物处理为自变量，怀孕时间gesttime为协变量

library(multcomp)
attach(litter)
head(litter)
table(litter$dose)fit <- aov(weight ~ gesttime + dose)
summary(fit)

在这里插入图片描述
ancova的F检验发现：gesttime怀孕时间与幼崽出生体重相关
控制怀孕时间，药物剂量与幼崽出生体重相关。
后续需要多重比较确定哪些药物剂量与幼崽出生体重显著相关。

我么可以获取去除协变量效应之后的组均值

library(effects)
effect("dose",fit)
aggregate(litter$weight,by=list(litter$dose),mean)

在这里插入图片描述

多重比较

tuk <- glht(fit,linfct = mcp(dose="Tukey"))
plot(cld(tuk, level=.05),col="lightgrey")

在这里插入图片描述

多重比较之手动设定contrast

library(multcomp)
contrast <- rbind("no drug vs. drug" = c(3, -1, -1, -1))
summary(glht(fit, linfct=mcp(dose=contrast)))

在这里插入图片描述

评估检验的假设条件

因变量的正态性

library(car)
qqPlot(lm(weight ~ gesttime + dose, data=litter),simulate=TRUE, main="Q-Q Plot", labels=FALSE)

在这里插入图片描述

分组间的方差齐性

bartlett.test(weight ~ gesttime, data=litter)
bartlett.test(weight ~ dose, data=litter[litter$dose !=0,]) #我发现加上0剂量的处理组，不同处理组的方差齐性原则遭到破坏了

离群点检验

library(car)
outlierTest(fit)

在这里插入图片描述

双因素方差分析

根据有没有重复观测值可以分为两种双因素方差分析。
没有重复观测值，则可以认为列变量重复了行变量次。
具有重复观测值，则可以认为列变量重复了对应的重复观测次。
当然了均衡设计和非均衡设计的方差计算方式也有差别。
双因素的互作项的方差不单独估计的话，会被归为误差。

没有重复观测值的双因素方差分析

在这里插入图片描述

attach(ToothGrowth)
table(supp, dose)dose <- factor(dose)#dose转为因子型变量，这样aov函数将其当作分组变量对待，否则会当成数值型协变量对待
fit <- aov(len ~ supp*dose)
summary(fit)

在这里插入图片描述
可以看到主效应和协效应的作用都很显著。

interaction.plot(dose, supp, len, type="b",col=c("red","blue"), pch=c(16, 18),main = "Interaction between Dose and Supplement Type")

在这里插入图片描述

library(HH)
interaction2wt(len~supp*dose)

在这里插入图片描述

均值比较

tuk <- glht(fit,linfct=mcp(supp="Tukey"))
plot(cld(tuk, level=.05),col="lightgrey")
summary(tuk)tuk <- glht(fit,linfct=mcp(dose="Tukey"))
plot(cld(tuk, level=.05),col="lightgrey")
summary(tuk)

评估检验的假设条件

正态性检验
方差齐性检验
离群点检验

library(car)
qqPlot(lm(len~supp*dose, data=ToothGrowth),simulate=TRUE, main="Q-Q Plot", labels=FALSE)bartlett.test(len ~ supp, data=ToothGrowth)
bartlett.test(len ~ dose, data=ToothGrowth)library(car)
outlierTest(fit)

具有重复观测值的双因素方差分析

attach(CO2)
head(CO2)
# 因变量是CO2的吸收量 uptake
# 自变量包括分组变量 Type，以及组内变量 CO2浓度 conc
table(CO2$Type)
table(CO2$conc)table(CO2$Type,CO2$conc)#均衡设计

在这里插入图片描述

拟合模型
这里需要注意的时，aov没有指定模型的参数，好像是默认为固定效应模型，
像随机模型和混合模型好像没法使用aov函数。

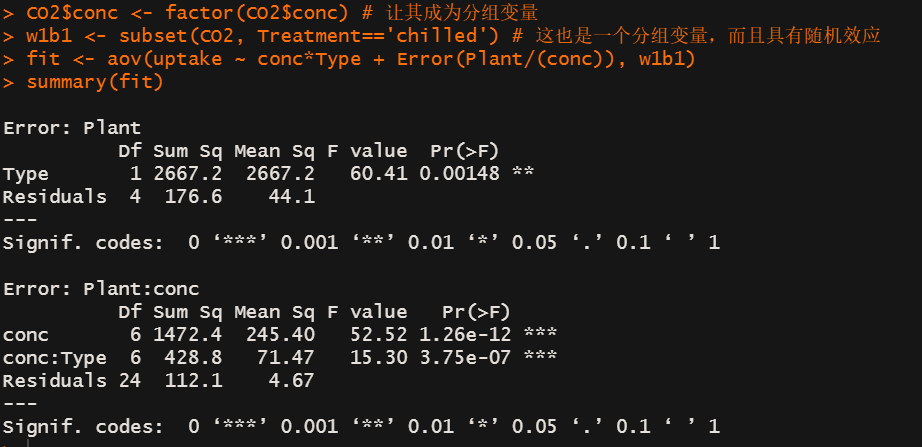
CO2$conc <- factor(CO2$conc) # 让其成为分组变量
w1b1 <- subset(CO2, Treatment=='chilled') # 这也是一个分组变量，而且具有随机效应
fit <- aov(uptake ~ conc*Type + Error(Plant/(conc)), w1b1) #subject是 Plant ；组内变量是conc
summary(fit)

在这里插入图片描述

均值比较

fit <- aov(uptake ~ conc*Type, w1b1)
summary(fit)tuk <- glht(fit,linfct=mcp(conc="Tukey"))
plot(cld(tuk, level=.05),col="lightgrey")
summary(tuk)tuk <- glht(fit,linfct=mcp(Type="Tukey"))
plot(cld(tuk, level=.05),col="lightgrey")
summary(tuk)

评估检验的假设条件

正态性检验
方差齐性检验
离群点检验

library(car)
qqPlot(lm(uptake ~ conc*Type, w1b1),simulate=TRUE, main="Q-Q Plot", labels=FALSE)bartlett.test(uptake ~ conc, data=w1b1)
bartlett.test(uptake ~ Type, data=w1b1)library(car)
outlierTest(fit)