题目

给你两个正整数 a 和 b ，返回 a 和 b 的 公因子的数目。
如果 x 可以同时整除 a 和 b ，则认为 x 是 a 和 b 的一个公因子

解析

这题本身显然是很简单的，只不过这里面有一个很古老的知识点，正好一起回忆一下，这就是辗转相除法。

辗转相除法

辗转相除法用于求两个数的最大公因子。形式化讲，辗转相除法的运行过程如下：

1. 确定两个正整数 a 和 b，其中 a 是大于 b 的。
2. 计算 a 除以 b 的余数 r。
3. 如果 r=0，则 b 就是 a 和 b 的最大公约数，算法结束。
4. 否则，将 b 赋值给 a，将 r 赋值给 b，并回到第二步。

这一套看完，用肯定是会用了，毕竟一步一步来就可以了，代码也很好写。但为啥这样就能求出最大公约数呢？我们用图来解释一下。

图示

1. 我们设要求的两个数分别为15和25

2. 用25除以15，余下10，我们可以看做就好像从25的方块中挖出一个10来

3. 用15除以10，余下5，就好像15中挖出5（这里开始我们不用数字来表示方块，简略的表示他们的大小关系）

4. 10除以5，我们发现余数为0，则25和5的最大公约数就是5
   

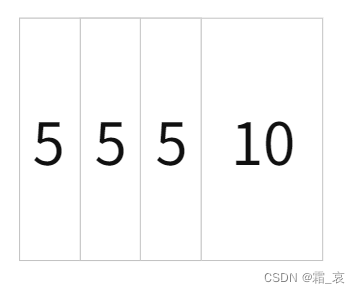
在这个过程中，我们实际上挖掉的是余数，而余数/余数=1，然后我们再用剩下的那一块/余数，相当于每次试图从被除数中挖出尽量多个余数。当余数为0时，我们认定上一轮的余数5可以将当前还没被挖的那一部分挖尽，所以被除数和除数都能整除这个余数，所以辗转相除法成立。

这道题中涉及到的比较重要的知识点大概就这一个，搞明白这一点，这道题也就没什么难的了。
最后，浅浅贴一下官方的代码：

代码

class Solution {
public:int commonFactors(int a, int b) {int c = gcd(a, b), ans = 0;//辗转相除法的函数gcdfor (int x = 1; x * x <= c; ++x) {if (c % x == 0) {++ans;if (x * x != c) {++ans;}}}return ans;}
};

总结

一道水题，可能是官方在清明节网开一面，想让大家休息休息吧。但辗转相除法还是比较重要的，有的时候可以有效优化时间复杂度。

我是霜_哀，在算法之路上努力前行的一位萌新，感谢你的阅读！如果觉得好的话，可以关注一下，我会在将来带来更多更全面的算法讲解！