为什么会使用KMP

在一个串中查找是否出现过另一个串，这是KMP的看家本领。那么寻找重复子串怎么也涉及到KMP算法了呢？

KMP算法中next数组为什么遇到字符不匹配的时候可以找到上一个匹配过的位置继续匹配，靠的是有计算好的前缀表。前缀表里，统计了各个位置为终点字符串的最长相同前后缀的长度。

那么最长相同前后缀和重复子串的关系又有什么关系呢。

可能很多录友又忘了前缀和后缀的定义，再回顾一下：

前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串；
后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串

在由重复子串组成的字符串中，最长相等前后缀不包含的子串就是最小重复子串，这里拿字符串s：abababab 来举例，ab就是最小重复单位，如图所示：

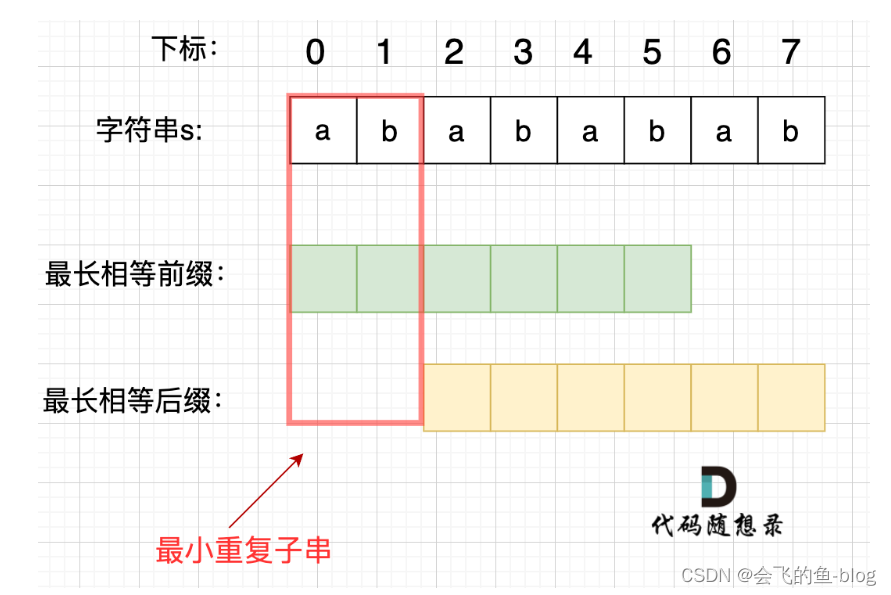
如何找到最小重复子串

步骤一：因为这是相等的前缀和后缀，t[0] 与 k[0]相同， t[1] 与 k[1]相同，所以 s[0] 一定和 s[2]相同，s[1] 一定和 s[3]相同，即：，s[0]s[1]与s[2]s[3]相同。

步骤二：因为在同一个字符串位置，所以 t[2] 与 k[0]相同，t[3] 与 k[1]相同。

步骤三：因为这是相等的前缀和后缀，t[2] 与 k[2]相同，t[3]与k[3] 相同，所以，s[2]一定和s[4]相同，s[3]一定和s[5]相同，即：s[2]s[3] 与 s[4]s[5]相同。

步骤四：循环往复。

所以字符串s，s[0]s[1]与s[2]s[3]相同， s[2]s[3] 与 s[4]s[5]相同，s[4]s[5] 与 s[6]s[7] 相同。

正是因为最长相等前后缀的规则，当一个字符串由重复子串组成的，最长相等前后缀不包含的子串就是最小重复子串。

简单推理

这里再给出一个数学推导，就容易理解很多。

假设字符串s使用多个重复子串构成（这个子串是最小重复单位），重复出现的子字符串长度是x，所以s是由n * x组成。

因为字符串s的最长相同前后缀的长度一定是不包含s本身，所以最长相同前后缀长度必然是m * x，而且 n - m = 1，（这里如果不懂，看上面的推理）

所以如果 nx % (n - m)x = 0，就可以判定有重复出现的子字符串。

next 数组记录的就是最长相同前后缀字符串：KMP算法精讲 (opens new window)这里介绍了什么是前缀，什么是后缀，什么又是最长相同前后缀)，如果 next[len - 1] != -1，则说明字符串有最长相同的前后缀（就是字符串里的前缀子串和后缀子串相同的最长长度）。

最长相等前后缀的长度为：next[len - 1] + 1。(这里的next数组是以统一减一的方式计算的，因此需要+1，两种计算next数组的具体区别看这里：字符串：KMP算法精讲 (opens new window))

数组长度为：len。

如果len % (len - (next[len - 1] + 1)) == 0 ，则说明数组的长度正好可以被 (数组长度-最长相等前后缀的长度) 整除，说明该字符串有重复的子字符串。

数组长度减去最长相同前后缀的长度相当于是第一个周期的长度，也就是一个周期的长度，如果这个周期可以被整除，就说明整个数组就是这个周期的循环。

强烈建议大家把next数组打印出来，看看next数组里的规律，有助于理解KMP算法

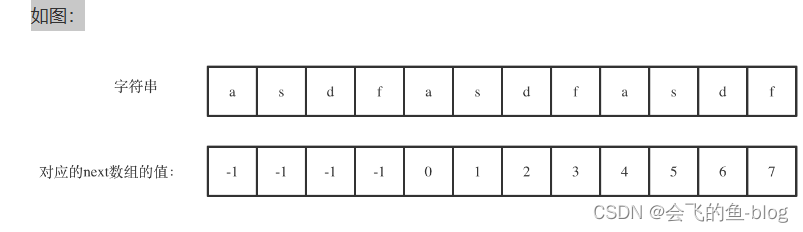
next[len - 1] = 7，next[len - 1] + 1 = 8，8就是此时字符串asdfasdfasdf的最长相同前后缀的长度。

(len - (next[len - 1] + 1)) 也就是： 12(字符串的长度) - 8(最长公共前后缀的长度) = 4， 4正好可以被 12(字符串的长度) 整除，所以说明有重复的子字符串（asdf）。

C++代码如下：（这里使用了前缀表统一的实现方式）

//第一种
// class Solution {
// public:
//     bool repeatedSubstringPattern(string s) {
//         string str = s + s;//         str.erase(str.begin()); 
//         str.erase(str.end() - 1);//         if(str.find(s) != std::string::npos)
//             return true;//         return false;
//     }
// };//第二种
class Solution
{
public:void getNext(int *next,const string &s){next[0] = 0;int j = 0;for(int i = 1; i < s.size(); i++){while(j > 0 && s[i] != s[j]){j = next[j - 1];}if(s[i] == s[j]){j++;}next[i] = j;}}bool repeatedSubstringPattern(string s){if(s.size() == 0){return false;}int next[s.size()];getNext(next,s);int len = s.size();if(next[len - 1] !=0 && len % (len - (next[len - 1])) == 0){return true;}return false;}
};