\qquad 本文以一维核平滑为例，假设有观测数据集 { x i , y i } i = 0 N , x i , y i ∈ R \{x_i,y_i\}_{i=0}^N\ ,x_i,y_i\in R {xi​,yi​}i=0N​ ,xi​,yi​∈R，目标是为了找到一个回归函数 $y=f(x)$ 来拟合观测数据。
\qquad

1. 核平滑方法

\qquad 核平滑$\text{(Kernel Smoothing)}$的基本思想：
$(1)$ 只使用与目标点 $x_i$ 邻近位置 x ∈ N i = { x ∣ ∣ ∣ x − x i ∣ ∣ < δ } x\in\mathcal N_i=\{x\ \big|\ ||x-x_i||<\delta\} x∈Ni​={x ∣ ∣​ ∣∣x−xi​∣∣<δ} 的一些观测点来进行拟合
$(2)$ 这种局部化是通过核函数 $\text{(kernel function)}$ 来刻画
\qquad\qquad 离目标点 $x_i$ 越近的观测点对 $x_i$ 的估计影响更大、具有更大的权值
\qquad\qquad 离目标点 $x_i$ 越远的观测点对 $x_i$ 的估计影响更小、具有更小的权值

\qquad 例如，图 $1$ 中的高斯核函数（其中 $h$ 为标准差，控制邻域宽度）

$K(x,x_i)=K(\parallel x-x_i\parallel )=e^{-\frac{(x-x_i{)}^2}{2h^2}},\forall x\in {\mathcal{N}}_i$

\qquad

图1 对于目标点为 $(x_i,y_i)$ 处的黑色实心点，$x$ 轴上的红色实心点表示与 $x_i$ 相邻的位置 $x\in {\mathcal{N}}_i$，红色空心点为 $x$ 轴上红色实心点对应的高斯权值
另外，图中还画出了一部分代表观测数据的黑色空心点处的高斯权值曲线

\qquad 核平滑，也就是局部加权平均，核回归函数为：

$y=f(x)=\frac{\sum _{i=0}^N{y}_{i}K(x,x_i)}{\sum _{i=0}^{N}K(x,x_i)}$

\qquad

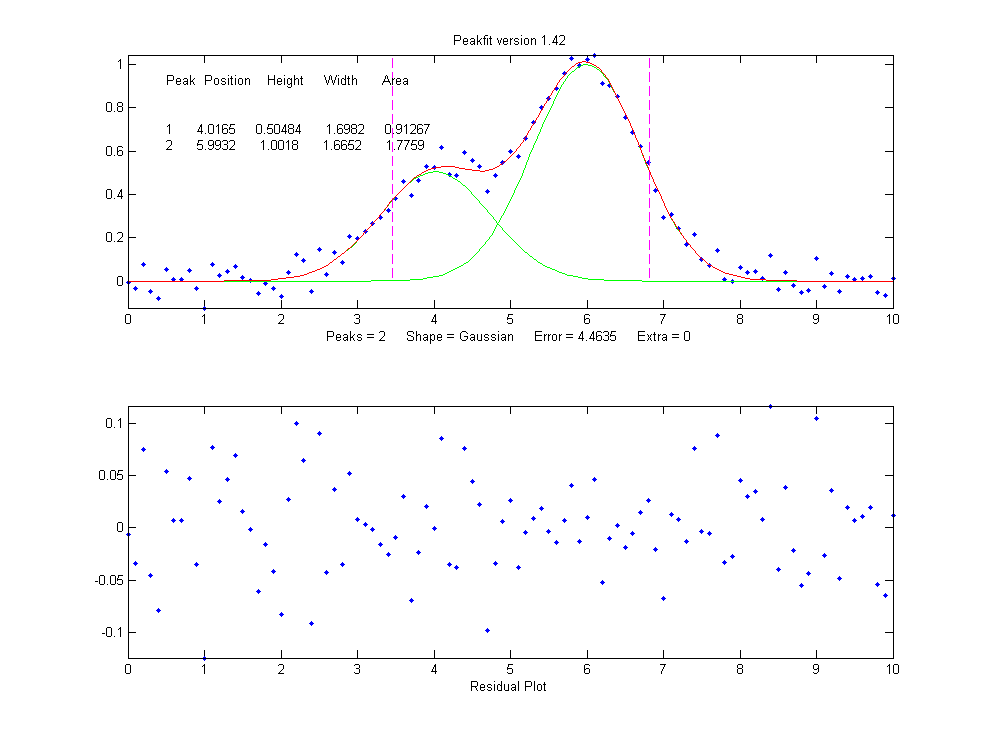
图2 常见的三种核函数：Epanechnikov和Tri-cube是紧支的，而Gaussian是非紧支的。
图片取自于《The Elements of Statistical Learning - Data Mining, Inference, and Prediction》Fig 6.2

$\text{Epanechnikov}$ 二次核：

$K(x,x_i)=D\left(\frac{\parallel x-x_i\parallel }{h}\right)$，其中 $h$ 确定 $x_i$ 的邻域宽度。

$D(t)=\{\begin{array}{cc}\frac{3}{4}(1-t^2)& ,|t|<1\\ & \\ 0& ,其他\end{array}$

$\text{Tri-cube}$ 核：

$D(t)=\{\begin{array}{cc}(1-|t{|}^3{)}^3& ,|t|<1\\ & \\ 0& ,其他\end{array}$

\qquad 显然，$h$ 值越小，相同情况下的 $t=\frac{\parallel x-x_i\parallel }{h}$ 越大，对于紧支撑的核函数 $D(t)$ 而言，用于实现局部加权平均的局部观测数据就越少。
\qquad 反之，$h$ 值越大，相同情况下的 $t=\frac{\parallel x-x_i\parallel }{h}$ 越小，参与局部加权平均的局部观测数据就越多。
\qquad

代码实现

import numpy as np
import matplotlib.pyplot as pltdef kernel_regression(x, h, h0):weight_e = lambda t:  (1-t**2)*3/4 weight_t = lambda t:  (1-t**3)**3 y = np.sin(4*x)y_noise = y + np.random.randn(len(x))/3num = len(x)y_rec_e = np.zeros(num)y_rec_t = np.zeros(num)y_rec_g = np.zeros(num)for i in range(num):dist = np.abs(x-x[i])/h  # epanechnikovw_e = weight_e(dist)*np.where(dist<=1,1,0)              y_rec_e[i] = np.sum(y_noise*w_e)/np.sum(w_e)# tri-cubew_t = weight_t(dist)*np.where(dist<=1,1,0) y_rec_t[i] = np.sum(y_noise*w_t)/np.sum(w_t)# gaussian kernel    gaussian_kernel = lambda d,h: np.exp(-dist**2/(2*(h**2)))/(np.sqrt(2*np.pi)*h)for i in range(num):dist = np.abs(x-x[i])w = gaussian_kernel(dist,h0)y_rec_g[i] = np.sum(y_noise*w)/np.sum(w)        return y_rec_g, y_rec_e, y_rec_t, y_noise, yif __name__ == '__main__':    plt.figuresnum = 100h = 0.3h0 = 0.1x = np.linspace(0,1,snum)y_rec_g, y_rec_e, y_rec_t, y_noise, y = kernel_regression(x,h,h0)plt.plot(x,y)plt.plot(x,y_noise,'yo',markerfacecolor='none')plt.plot(x,y_rec_e,'k')plt.plot(x,y_rec_t,'r')plt.plot(x,y_rec_g,'m')    plt.legend(labels=['original data','noise data','epanechnikov','tri-cube','gaussian'],loc='upper right')plt.title('kernel regression:y=sin(4x),h=0.3') plt.show()

运行结果：
\qquad
\qquad
\qquad

数据集不同时，$h$ 的值也要进行相应调整。

\qquad

2. 局部多项式核回归

\qquad 由于核函数在边界区域上无法满足对称性（例如，图$1$中左侧边界点 $x=-4$ 处只有右侧邻域中的观测点可以用，右侧边界点 $x=4$ 处只有左侧邻域中的观测点可以用），局部加权平均在边界处会出现较大的误差（如上图所示），局部多项式回归可以缓解这一问题。

2.1 加权最小二乘法(Weighted least squares)

\qquad 如下图所示，已知观测样本集 { x i , y i } i = 0 N \{\boldsymbol x_{i},y_{i}\}_{i=0}^{N} {xi​,yi​}i=0N​，采用线性模型：

\qquad\qquad $\begin{array}{rl}\phi (\mathbf{x})& =\sum _{n=0}^M{a}_n{\phi }_n(\mathbf{x})=a_0{\phi }_0(\mathbf{x})+a_1{\phi }_1(\mathbf{x})+\cdots +a_M{\phi }_M(\mathbf{x})\\ & ={\mathbf{\theta }}^T\mathbf{\varphi }(\mathbf{x})={\mathbf{\varphi }}^T(\mathbf{x})\mathbf{\theta }\end{array}$

\qquad 其中，$\mathbf{\theta }=[a_0,a_1,\cdots ,a_M{]}^T$，$\mathbf{\varphi }(\mathbf{x})=[{\phi }_0(\mathbf{x}),{\phi }_1(\mathbf{x}),\cdots ,{\phi }_M(\mathbf{x}){]}^T$

\qquad
\qquad 上图中，线性模型关于每个观测点 $({\mathbf{x}}_i,y_i)$ 的 ${\ell }_2$ 损失（平方误差）为：$[\phi ({\mathbf{x}}_i)-y_i{]}^2$

\qquad 假设每个观测点的对误差的影响各不相同，因此，引入加权系数 { w i } i = 0 N \{w_i\}_{i=0}^{N} {wi​}i=0N​，将“整个数据集的总误差”设为加权损失函数 $\text{(weighted loss function)}$，也就是：

\qquad\qquad $\begin{array}{rl}J(\mathbf{\theta })& =w_0[\phi ({\mathbf{x}}_0)-y_0{]}^2+w_1[\phi ({\mathbf{x}}_1)-y_1{]}^2+\cdots +w_N[\phi ({\mathbf{x}}_N)-y_N{]}^2\\ & =\sum _{i=0}^N{w}_i[\phi ({\mathbf{x}}_i)-y_i{]}^2\\ & =\sum _{i=0}^N{w}_i[{\mathbf{\theta }}^T\mathbf{\varphi }({\mathbf{x}}_i)-y_i{]}^2\\ & =(\Phi \mathbf{\theta }-\mathbf{y}{)}^{T}W(\Phi \mathbf{\theta }-\mathbf{y})\end{array}$

\qquad 其中，$\mathbf{y}=[y_0,y_1,\cdots ,y_N{]}^T$

\qquad 　　　$W=\left[\begin{array}{cccc}{w}_0& & & \\ & w_1& & \\ & & \ddots & \\ & & & w_N\end{array}\right]$

\qquad 　　　$\Phi =\left[\begin{array}{c}\mathbf{\varphi }({\mathbf{x}}_0{)}^T\\ \mathbf{\varphi }({\mathbf{x}}_1{)}^T\\ ⋮\\ \mathbf{\varphi }({\mathbf{x}}_N{)}^T\end{array}\right]=\left[\begin{array}{cccc}{\phi }_0({\mathbf{x}}_0)& {\phi }_1({\mathbf{x}}_0)& \cdots & {\phi }_M({\mathbf{x}}_0)\\ {\phi }_0({\mathbf{x}}_1)& {\phi }_1({\mathbf{x}}_1)& \cdots & {\phi }_M({\mathbf{x}}_1)\\ ⋮& ⋮& & ⋮\\ {\phi }_0({\mathbf{x}}_N)& {\phi }_1({\mathbf{x}}_N)& \cdots & {\phi }_M({\mathbf{x}}_N)\end{array}\right]$
\qquad
\qquad 损失函数 $J(\mathbf{\theta })$ 对系数 $\mathbf{\theta }$ 求偏导：

\qquad\qquad $\begin{array}{rl}\frac{\partial J(\mathbf{\theta })}{\partial \mathbf{\theta }}& =2{\Phi }^{T}W\Phi \theta -2{\Phi }^{T}W\mathbf{y}=0\end{array}$

\qquad 可求得：

\qquad\qquad $\mathbf{\theta }=({\Phi }^{T}W\Phi {)}^{-1}{\Phi }^{T}W\mathbf{y}$
\qquad
\qquad 关于本节内容更详细的解释，请参考《函数的最佳逼近问题：最小二乘法》
\qquad

2.2 局部多项式核回归(Local polynomial kernel regression)

\qquad 局部加权回归，是在每个目标点 $x_i$ 单独求一个加权最小二乘解。

\qquad 若最小二乘逼近采用多项式模型：

\qquad\qquad $\begin{array}{rl}\phi (x)& =\sum _{n=0}^M{a}_n{\phi }_n(x)=a_0{\phi }_0(x)+a_1{\phi }_1(x)+\cdots +a_M{\phi }_M(x)\\ & =a_0+a_{1}x+a_2{x}^2+\cdots +a_M{x}^M\\ & =\sum _{n=0}^M{a}_n{x}^n\end{array}$

\qquad\qquad 也就是：${\phi }_0(x)=1$ 和 ${\phi }_n(x)=x^n,n=1\sim M$

\qquad 特别地，当 $M=1$ 时，多项式模型就变成了线性回归模型。
\qquad 　　　　当 $M=2$ 时，多项式模型就变成了抛物线回归模型。

\qquad 因此，局部加权回归可以描述为：
$(1)$ 采用$M$阶多项式模型来求加权最小二乘解
$(2)$ 采用高斯核函数 $K(x,x_i)=K(\parallel x-x_i\parallel )$ 来刻画目标点 $x_i$ 的邻域位置 x ∈ N i = { x ∣ ∥ x − x i ∥ < δ } x\in \mathcal N_i=\{x\ \big|\parallel x-x_i\parallel\ <\delta\} x∈Ni​={x ∣ ∣​∥x−xi​∥ <δ} 处观测数据的权值，作为加权最小二乘解中的权值

\qquad 也就是求每个观测点 $x_i$ 的加权最小二乘解，此时的目标函数为：

\qquad\qquad $\begin{array}{rl}{J}_i(\mathbf{\theta })& =\sum _{x_j\in {\mathcal{N}}_i}K(x_i,x_j){\left[y_j-\sum _{n=0}^M{a}_n(x_i)x_j^n\right]}^2\\ & =\sum _{x_j\in {\mathcal{N}}_i}K(x_i,x_j)[y_j-{\mathbf{\theta }}_i^T\mathbf{\varphi }(x_j){]}^2\end{array}$

\qquad 其中，${\mathbf{\theta }}_i=[a_0(x_i),a_1(x_i),a_2(x_i),\cdots ,a_M(x_i){]}^T$，$\mathbf{\varphi }(x)=[1,x,x^2,\cdots ,x^M{]}^T$

\qquad 因此，对观测点 $x_i$ 的（关于局部数据集的）目标函数 $J_i(\mathbf{\theta })$ 可求出在观测点 $x_i$ 的加权最小二乘解 ${\mathbf{\theta }}_i$，也就是用与观测点 $x_i$ 邻近的局部观测数据来拟合局部曲线。

\qquad 局部多项式核回归的示意图如图 $3$ 所示：
\qquad

图3 在目标点为 $(x_i,y_i)$ 处的局部多项式核回归示意图（假设蓝色曲线为“局部多项式核回归”的结果）
（1）待求解的黑色实心点目标值 $y_i$ 对应于 $x$ 轴的位置为黑色空心点 $x_i$
（2）在示意图中，使用了 $x_i$ 位置的左边和右边的 $4$ 个邻近位置的观测数据（红色实心点）作为“局部观测数据集” ${\mathcal{N}}_i$，来求加权最小二乘解 $\tilde{f}(x)$
（3）各个局部观测数据 $x\in {\mathcal{N}}_i$ 的权值由高斯核函数求得，即图中的“+”号所表示的
（4）将局部多项式核回归的解 $\tilde{f}(x_i)$ 作为黑色空心点位置 $x_i$ 的目标值，即 $y_i=\tilde{f}(x_i)$

代码实现

import numpy as np
import matplotlib.pyplot as pltdef gen_data(x):y = x ** 2 + 30 * np.sin(x)y_noise = y + np.random.randn(len(x))*5return y, y_noise#基于多项式模型的加权最小二乘法
def weighted_least_squares(y_noise,x,M,W):    design_matrix = np.asmatrix(np.ones(len(x))).Tfor i in range(1,M+1):arr = np.asmatrix(np.power(x,i)).Tdesign_matrix  = np.concatenate((design_matrix ,arr),axis=1)    coef = (design_matrix.T*W*design_matrix).I*(design_matrix.T*W*(np.asmatrix(y_noise).T))    return np.asarray(coef)def local_polynomial_kernel_regression(y_noise,x,M,width,sigma):kernel = lambda x,c,sig: np.exp(-(x-x[c])**2/(2*(sig**2)))/(np.sqrt(2*np.pi)*sig)for i in range(len(x)):local_y = y_noise[max(0,i-width):min(len(x),i+width)] local_x = x[max(0,i-width):min(len(x),i+width)]weight = kernel(x,i,sigma)#计算邻域各位置的权值local_weight = weight[max(0,i-width):min(len(x),i+width)]W = np.diag(local_weight)coef = weighted_least_squares(local_y,local_x,M,W)if M==1:#局部线性回归y[i] = coef[1]*x[i] + coef[0]if M==2:#局部二阶多项式回归y[i] = coef[2]*x[i]*x[i] + coef[1]*x[i] + coef[0]        return y    if __name__ == '__main__':    plt.figurex = np.linspace(-8, 6, 200)y, y_noise = gen_data(x)plt.plot(x,y,'b')plt.plot(x,y_noise,'yx')y_rec = local_polynomial_kernel_regression(y_noise,x,1,20,0.8)#M=1线性plt.plot(x,y_rec,'r')y_rec = local_polynomial_kernel_regression(y_noise,x,2,20,0.8)#M=2二阶多项式plt.plot(x,y_rec,'k')plt.legend(labels=['original data','noise data','local linear','local polynomial'],loc='upper right')plt.title('local polynomial kernel regression')plt.show()

运行结果：
\qquad
\qquad 从上图中可以看出，与第1节核平滑方法中的“局部加权平均”的核回归方法相比，局部多项式回归在左右边界点处的拟合明显更好。