Curve fitting C: Non-linear Iterative Curve Fitting 
(a.k.a. "spectral deconvolution" or "peak deconvolution")

链接参上：http://terpconnect.umd.edu/~toh/spectrum/CurveFittingC.html

support  by 百度翻译 

translate by Xu__Jiayu  

***********************************

书到用时方恨少，以为最小二乘法是学过的，结果数值计算的那一个章节是叉掉的。

概率论与数理统计、数值计算、数据挖掘、高数（积分微积分）、线性代数、物理（震荡，甚么阻尼啊、波的叠加啊）

学的时候很专业，考的分数很专业，忘的时候更是专业到家。

我的智慧不如众人的智慧，但是众人的智慧终归不是我的智慧。

我想站在巨人的肩膀上，我想简单学着怎么用，结果发现连梯子的路口也没有找到。太尴尬了。---Xu__Jiayu

原文链接很多，我这里只放了小部分。链接里面都是资源啊！！！

**************************************

最小二乘法曲线拟合又名曲线拟合A,是最简单最快速的，但是他依赖于变量可以被建模成线性多项式。

我们了解到在某些情况下，非线性的可以通过坐标系的变换转化为线性的，但是这也是在某些特殊情况下，

他会限制相关数据的取值范围。不管何种情况，数据通过坐标转换后会有一些噪声点会使得用这种方式测得的参数不准确。

数据集拟合任何模型的最一般的方法就是迭代法。在不断“试验与错误”的过程，整体低对参数不断调整，直到拟合达到近似要求。

这是蛮力的方式。在电脑出现以前，这种方法仅能勉强使用。随这计算机计算速率和算法效率提高，迭代法比以前使用更广泛。

迭代法的一般过程

（1）为数据选一种模型

（2）初步估测出所有的非线性参数

（3）计算程序估算模型并对比数据集，估测拟合误差

（4）如果拟合误差大于拟合需求精度，程序会整体改变参数并返回会上一步。而后继续循环拟合直到迭代次数达到最大要求或者拟合精度达到要求。

这样继续直到拟合误差小于指定的误差。在这技术领域有一个很有名的叫做Nelder-Mead单纯形算法。（步骤（4））本质是对参数的组织和优化，

以缩短拟合达到精度要求所消耗的时间。用现在的个人电脑，整个过程可能就一秒或几秒的时间，这主要取决于模型的复杂度以及模型中调整的参数数目。

右边的图片展示了由两个峰由高斯去拟合的一小部分x关于y的数据的迭代过程。为了利于观察，人为的放慢拟合速度，在标准的台式机上通过一步一步的

plot绘出来的图像，初始用了最坏的猜想以及增加pause()停顿大约0.06秒。

迭代方法中主要的问题是有时候不会收敛得到一个最佳结果。解决的方法是重新使用算法，使用另一组初始化猜测。

重复几次，采用那组拟合误差最小的。（在下面介绍的peakfitting峰拟合函数中这个过程是自动进行的）。曲线迭代拟合

比线性回归在个人电脑上需要花费更多的时间。曲线迭代一秒完成的一部分，线性回归可能几毫秒就完成了，但是，

这个速度对某些用途就足够用了。

模型参数精度在拟合过程中的测量，例如最经典的最小二乘法模型的拟合强度，信噪比、拟合成功的数据点的数量，这是需要计算的。

使用代数方法根据预测计算的模型参数的标准差是不实际的，而蒙特卡洛模拟和引导方法都适用。

注：术语‘解谱’或‘带解卷积’在这技术领域经常涉及到，在这边文章里面的另一部分，“解卷积”作为独立概念特指傅立叶解卷积。

在傅立叶解卷积中，峰谷形状是未知的但是宽假定为已知。在最小二乘法的曲线迭代拟合中是相反的，峰的形状已知而宽是未知的，

扩张取决于数据中峰形状和宽度。因此，解谱是不明确的，可能代表从频谱到傅立叶解卷积（频谱的傅立叶变换）或者

可能代表把频谱分解成由多个峰组成。这是个不同的过程，不要混淆。看AppendixH附录H：傅立叶解卷积和曲线拟合。

--------------------------------------------------------------------------------------------

电子制表软件和独立程序

EXCEL和OpenOfficeCalc都有通过改变指定的单元格达到目的的“解”的能力。这个可以在峰拟合中可以用于减少

数据集和计算估测模型之间的拟合误差，例如重叠的高斯带。最新版本有三种不同的解决方法。EXCEL样例截图如下：演示了如何用4个高斯分
量拟合列A和列B分别行数22到101对应x和y数据样本集。【注(A22:A101)(B22：B101)你可以把你的数据带入样例中。原文提供文件链接】

输入数据后，眼睛感觉下大概几个高斯峰能代表这些数据以及他们的位置和宽度，输入这些值到建议模型表中（Proposed model）。电子表格
计算最佳拟合峰值（利用多元线性回归）采用估计振幅表和绘制数据拟合（调整图标的x轴刻度来适应数据）。下一步使用求解函数微调组分
（每个单高斯）的位置和宽度（图红线）从而减少拟合误差，并尽可能使得绘制的残差图（residual plot）尽可能随机分布：点击数据顶部
菜单栏，点击右上角的解决(Solver)打开解决箱（Solver box），在类型处Set Objective键入‘C12’，再点击‘小’（min）。在选择
模型（proposed model）中选择你想要的，在约束框（Subject to the Constrains）中加入约束条件【注：例如迭代次数或精度】，点击
解决按钮（Solve button）。所有组分的位置、宽度、峰值将会自动优化拟合并展示（你可以在模型表（proposed model）看到解的变换
选择初始参数减少拟合误差（单元格C12，红色））并是的残差减少且分布随机。）如果拟合失败，需要更改初始值，并点击解算器，点击
解按钮。你可以使用宏把上面合成一个按钮，使得上述过程自动化。如附录N所述。

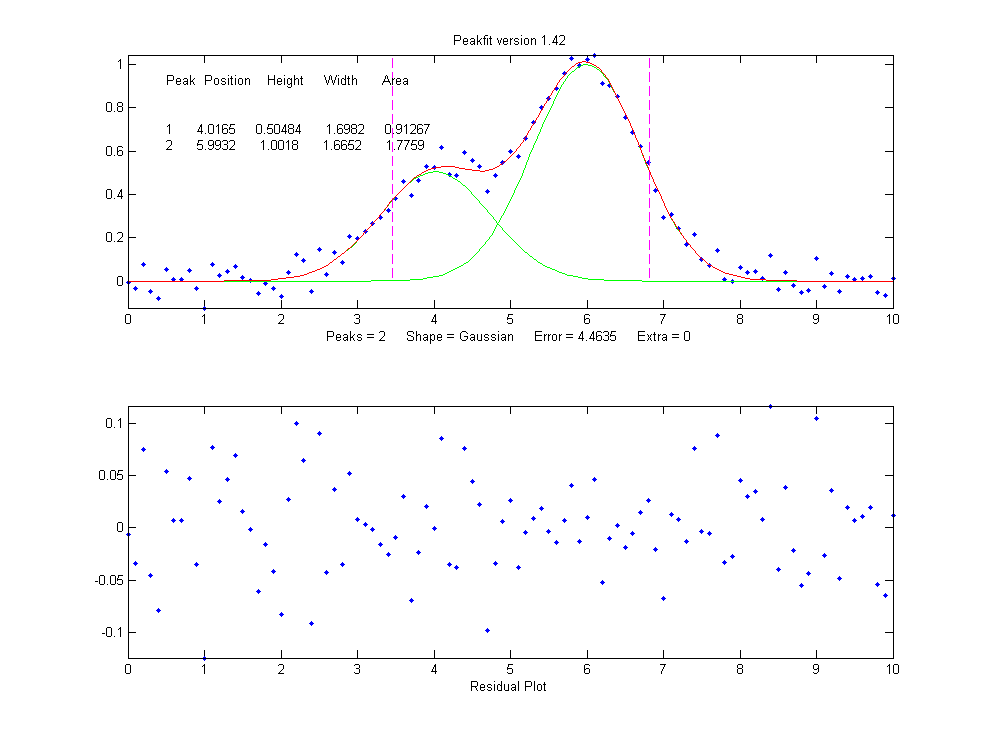
那么，需要多少个高斯分量来拟合数据呢？一个告诉的方法是看残差图（显示数据和拟合模型之间的点对点差异），并添加组分，直到残差是随机的，而不是波浪形的，但只有拟合前当数据是不平滑的才能这样做。这里有一个例子：用两个、三个、四个、五个高斯拟合递增序列的实数的数据集。正如你所看到的这个序列截图，你会看到百分比拟合误差降低，R2值更得接近1，残差变得更小，更随机。（注意在5个组分的配合，第一个和最后一个组分在250-600 x范围没有峰内的数据，而在背景上有）。没有必要去试6个组分的拟合，因5个组件的残差已经随机分布，更多个的组分“拟合噪声”且可能更不稳定，给出一种带有各种噪声的很不一样的结果。

Excel和OpenOffice有许多可下载的非线性迭代拟合曲线的插件和宏，还有一些独立的免费商业程序进行优化。例如，伦敦大学玛丽皇后RogerNix博士开发了一个非常好的EXCEL和VBA的电子制表软件针对X射线光电子能谱（XPS）进行曲线拟合，但也可以用来拟合其他类型的光谱数据。一个4页指令表也提供了。http://www.chem.qmul.ac.uk/software/eXPFit.htm

如果你使用一个电子表格来做曲线拟合，你必须为每个问题指定一个电子表格，正确的数据行数和希望拟合的组分个数。例如CurveFitter.xlsx只有100个信号点和5个高斯，通过简单在22到100行插入行来获得适应更大的数据点，并列向的拖动复制公式到新的单元格。（例如 CurveFitter2.xlsx 是扩展到256个数据点的）。为了处理其他数量的组分或模型形状，你需要在C和G之间、在Q和U之间插入或删除列，并编辑公式，因为当前模版只针对2个、3个、4个、5个、6个的高斯组分设置的。

如果峰在一个基线叠加，你可以包含把基线作为一个组分。例如你在线性斜坡基线上拟合两个高斯峰。为电子表模版选择三个组分，并改变一个原来的高斯组分为直线方程y=mx+b，m是斜率，b是截距。这种情况的模版http://terpconnect.umd.edu/~toh/spectrum/CurveFitter2GaussianBaseline.xlsx
不要点击“使无约束变量为负（Make Unconstrained Variables Non-Negative）”，因为基线模型可能需要负变量。如果你想使用另一种峰的形状或另一种基线形状，你必须在修改行22对应列C到G的方程，并拖动修改列向到最后一行。高斯峰为洛伦兹形状的http://terpconnect.umd.edu/~toh/spectrum/CurveFitter6Lorentzian.xlsx
或者你可以使C到G列包含不同的峰或基线形状的方程。

重点是，实际上你可定制编辑获得一个电子表格模版去拟合你的数据。相比之下，我的MATLAB/OCTAVE peakfit.m函数自动适应任何数量的数据点，并且很简单通过改变输入参数设置40种以上不同模型峰形状和任意峰数量。通过在matlab使用ipf.m，你可以按一个键立即改变峰的形状、峰的数量、基线模型，或重新计算拟合数据子集的不同启动或引导程序。这比电子表格快很多。但是另一方面，这个电子表格应用程序更实用的优势是你可以相对简单的增加你自己制定的形状函数和约束，即使是使用标准的电子表格构造的复杂的公式。如果你在招聘助理，一个经验丰富的电子表格工程师会比matlab的更容易找。所以，如果你不确定要使用哪个，我建议你两种都试一下，再做决定。

------------------------------------------------------------------------------------------

有一个方便快捷的功能叫做“fminsearch”利用的是Nelder-Mead单纯形方法。它最初被设计为求函数的最小值，但它可以通过创建一个匿名函数应用于最小二乘曲线拟合（又名lambda函数）计算模型，比较它的数据，并返回拟合误差。例如写 parameters = fminsearch(@(lambda)(fitfunction(lambda,x,y)),start)用之前创建的fitfunction函数执行向量数据x和y的来迭代拟合一个模型，以第一个猜想作为起始。最佳拟合模型的参数会返回到向量“parameters”，以同样的顺序在“start”里面出现。

注：对于Octave用户，fminsearch函数包含了“Optim”在附加的包里面。（使用最新的版本1.2.2）从OctaveForge下载http://downloads.sourceforge.net/octave/optim-1.2.1.tar.gz?download。
建议把所有的附加包全部下载安装以备所需。按照OctaveForge网页介绍说明。而对于matlab用户，fminsearch是内置函数。虽然有许多其他可选的优化工具箱的优化程序，但这不是本文档中的例子和程序所需要的。

一个简单的例子，针对体白炽的光谱拟合黑体方程，以达到估计色温的目的。在这种情况下，只有一个非线性参数-温度。脚本BlackbodyDataFit.m http://terpconnect.umd.edu/~toh/spectrum/BlackbodyDataFit.m展示了该技术，把实验测得的光谱的向量组“波长”和“光辉”，调用fmisearch搭配拟合函数fitblackbody.m http://terpconnect.umd.edu/~toh/spectrum/fitblackbody.m（如果黑体辐射源热不均匀，它可以建模为两种或以上不同温度的和，样例在fitshape1.m的样例3）http://terpconnect.umd.edu/~toh/spectrum/fitshape1.m

另一个应用通过matlab内置的样例firdemo.m演示。其相应的拟合函数fitfun.m是两个指数衰减模型的和。想要看，只要在matlab命令行窗口键入“fitdemo”就可以。（Octave没有相应的演示功能） 

峰拟合。许多一起对产生的信号的测量方法是以各种形状的峰形式。有一个共同的需求就是要测点峰的位置、高度、宽度或者区域。即使他们是噪声或者重叠。这种不能用线性最小二乘法做，因为信号模型不能建模为线性系数多项式（峰的位置、宽度是不是线性函数），因此采用迭代曲线拟合技术，经常使用高斯、洛伦兹或其他的一些简单峰形状作为模型。

matlab/octave演示脚本Demofitgauss.m  http://terpconnect.umd.edu/~toh/spectrum/Demofitgauss.m
通过拟合函数fitgauss.m http://terpconnect.umd.edu/~toh/spectrum/fitgauss2.m 对一个数据集拟合一个高斯。这种情况下有两个非线性参数：峰的位置和峰的宽度（峰值是线性参数，由拟合函数fitgauss.m第9行的单步回归确定，并返回全局变量‘c’）。和简单的最小二乘法测量峰相比，迭代的方法优势在于使用了所有的数据点穿过整个峰，包括0和负点，可以应用与大量的重叠峰，在Demofitgauss2.m有展示http://terpconnect.umd.edu/~toh/spectrum/Demofitgauss2.m（图为了适应基线改变的可能性。我们在A矩阵中增加了一列1s），就像CLS方法那样。是一个额外峰值的效果模型，只有幅值没有位置和宽度。基线复制会随着峰值高度返回到全局变量向量'c'中。Demofitgaussb.m and fitgauss2b.m 加了这个附加. (Demofitlorentzianb.m and fitlorentzianb.m 是针对洛伦兹峰的)

这个使用相同的拟合函数fitgauss.m的峰拟合技术很容易扩展到任意数目的重叠峰，适应任何数目的峰也是简单的。根据第一次猜想的开始向量lambda随着向量t和y作为为函数的输入。
 function err = fitgauss(lambda,t,y)
 %   Fitting functions for a Gaussian band spectrum.
 %  T. C. O'Haver, 2006   Updated to Matlab 6, March 2006
 global c
 A = zeros(length(t),round(length(lambda)/2));
 for j = 1:length(lambda)/2,
     A(:,j) = gaussian(t,lambda(2*j-1),lambda(2*j))';
 end
 c = A\y';%
 z = A*c;
 err = norm(z-y');%拟合误差

如果在模型中有n个峰，那么lambda的长度是2n，每个迭代变量一个条目（[位置1 宽度1 位置2 宽度2...等]），循环中构建了n*length（t）的矩阵。包含了分离的峰的模型，可以使用用户定义的峰的函数。（使用gaussian.m），然后通过n个峰值向量c对比最小二乘回归，使用matlab的斜切符号‘\’。通过算出来的峰值用来计算z，n个峰值的总和。通过矩阵相乘，得到拟合误差--模型的z和实际的y之间的的平方差。返回到函数fminsearch，并多次调用这个过程，尝试不同的峰位峰宽，直到误差足够小。

这个拟合函数被matlab的fminsearch调用，如params=fminsearch(@(lambda)(fitgauss(lambda,x,y)),[50 20])。

在方括号中包含的每个峰的位置和宽度的第一猜测向量（[位置1 宽度1 位置2 宽度2...等]...等）。输出参数“params”返回最适合的每个峰的位置和宽度值的2×n矩阵，和峰值高度中的全局变量向量n长度的C。 相同的拟合函数可以为其他峰形状简单地调用相应的峰形函数定义，如洛伦兹 lorentzian.m 。（注：为了和其他类似的脚本Demofitgauss.m or Demofitgauss2.m 你的版本的MATLAB上运行，他们所有的调用函数必须加载到MATLAB，在这种情况下 fitgauss.m and gaussian.m的脚本调用的子函数必须在MATLAB的路径有。另一方面，可以有其所需的子函数定义在主函数本身，因此可以是自包含的，如下两个例子）。

fitshape2.m ([Positions,Heights,Widths,FittingError]=fitshape2(x,y,start)) 把这一切简化成了一个通用的MATLAB /Octave函数对数据包含矢量变量x和y拟合多重重叠模型形状。该模型为各个形状的基峰对应数学上定义的x的函数的加权和，程序独立确认两个变量峰值和宽度从而确认每个峰，峰值是加权权重的综合。你需要指定初始猜想（[位置1 宽度1 位置2 宽度2...等]）。函数返回的最佳拟合模型参数向量的位置、峰值、宽度，并计算百分误差数据和模型之间的拟合误差。绘制数据作为一个点，而拟合模型作为一条线。这个函数的有趣之处是，定义模型形状的唯一部分是最后一行。fitshape2.m，在那一行定义了高斯单元峰值的表达，你可以改变为其他报答或算法，计算g作为一个函数，关于x以及两个未知参数‘位置pos’和‘宽度wid’（他们可以代表其他的函数类型，指数脉冲，s型等）同fitshape.m一样。这使得fitshape是一个很好的平台用于试验不同的数学表达式作为模型目标拟合数据。这里还有两个其他变化的函数，一个迭代变量的加峰值fitshape1.m和三个迭代变量的加峰值fitshape3.m，每个都有说明性例子。

可变形状类型，例如沃伊特轮廓(Voigt),皮尔逊（Pearson），BWF线型拟合G峰（斜Lorentzian，也称为Breit-wigner-Fano），混合高斯-洛伦兹（Gauss-Lorentz blend），指数扩大高斯-洛伦兹（exponentially-broadened Gaussian and Lorentzian），不是只定义了 峰位，峰值，宽度，还额外定义了参数对峰的形状进行了调整。如果这参数在一个组的峰中都是等量和已知的，这个参数就可以作为一个额外的输入参数传递给形状函数，例如VoigtFixedAlpha.m中的。如果形状参数根据迭代而变化，且对组中的峰是不同（如位置和宽度）。程序必须修改迭代变量适应这三个，而不是两个，例如VoigtVariableAlpha.m。拟合误差会随着变量阿尔法（alphas）变小，但由于数据中的噪声点、初始的猜测以及大量的峰，程序执行进行中阿尔法的值走向是不稳定（这里有独立的函数）。Matlab/Octave版本7的函数peakfit.m对于皮尔逊、指数加宽高斯、沃伊特、混合高斯洛伦兹以及3个参数的逻辑斯迪克（logistic，虫口模型）或冈珀茨（Gompertz） 函数，三个参数分别是Bo、Kh、L而不是位置宽度和形状因子。


如果你不知道你的峰的形状，你可以采用peakfit.m或者ipf.m尝试一下不同的形状看看哪一个程序中的形状适合去拟合你的数据，试着找到这种峰对你的数据是经典的、分离良好且有比较好的信噪比。例如matlab的函数ShapeTestS.m和ShapeTestA.m 测试输入参数x和y，假设是单一的峰，使用peakfit.m用不同的候选模型峰来拟合，每个拟合分别单独绘制于不同的窗口，并在命令窗口输出拟合误差。我在ShapeTestS.m尝试了7种不同的候选峰，而ShapeTextA.m尝试了6种不同的候选峰。拟合误差最低（R2最接近1）的可以推测是最好的候选峰。每个函数的帮助文件都有尝试范例。但是需要注意，如果你的数据噪声点太多，结果可能是有误的、例如实际峰形可能是其他的而不是高斯。多元高斯模型可能拟合更高因为有更多的自由度来“拟合噪声”。matlab的函数peakfit.m有很多的内置形状可以选择，但是可选的还是有限的。有可能实际的峰在这个里面是没有的或者根本就不能简单的用数据函数来描述。


一个信号的不同形状的峰可以通过拟合函数fitmultiple.m,一个输入参数是峰类型的序列向量，一个是峰的形状参数的序列向量。峰类型和峰形状参数的序列需要视线决定好。怎么使用参照Demofitmultiple.m


你可以根据你的意图创建你自己的拟合函数，并没有限制是一个单一的代数表达式，可以是任意的复杂多步的算法。例如，在定量吸收光谱的TFit法，仪器扩展透射谱模型去拟合观测的投射数据，这种模型的拟合函数是投射谱的傅立叶卷积以及已知的光谱仪的狭缝函数。计算吸收度的方法是可选的，允许优化信噪比、延伸动态范围和线性校准远超正常范围的吸收光谱。


通过自主抽样法利用最小二乘法估测峰的参数是不确定。关于这个的一个简单的证明，Matlab/Octave的"BootstrapIterativeFit.m"函数提供的一个简单噪声高斯峰，可以通过这个提取单一的x，y的简单高斯噪声峰的数据集作为样本，利用迭代去拟合每个样本，利用峰高、峰位、宽度绘制出引导样本的直方图，语法是 BootstrapIterativeFit(真实高度, 真实位置, 真是宽度,样点数 , 噪声, 试验数) 真是高度是高斯峰值，真是位置是高斯峰值位置x轴对应的值，真实宽度是峰的半高宽，样点数是最小二乘法拟合用得数据点数，噪声是标准偏差（正态分布）的随机噪声，试验数是引导样本的数据点数。典型样例BootstrapIterativeFit(100,100,100,20,10,100); 如图所示

********************

略掉一部分样例没有翻译

********************

峰值拟合函数和脚本使用了一个非线性优化算法去把一个复杂的重叠峰的时间序列信号分解成组分峰。目的是确定你的信号可以由许多基峰的和组成。这个函数可接受任意长度，包括非整数和不均匀的x值。可以拟合任何数量的峰--高斯、等宽高斯、固定宽度高斯、指数扩大高斯、指数扩大等宽高斯、高斯岔、洛伦兹、固定宽度洛伦兹、等宽度洛伦兹、指数扩大洛伦兹、洛伦兹岔、罗基斯迪克（logistic ）分布、罗基斯迪克函数、三角、阿尔法函数、皮尔逊函数、皮尔逊7、指数脉冲、增S型生长曲线(up sigmoid),降S型生长曲线、高斯洛伦兹混合、BWF线型拟合G峰、沃伊特(Voigt)轮廓。这里有基本可用的峰的图形
http://terpconnect.umd.edu/~toh/spectrum/ShapeDemo.png


这里有两个版本。一个是命令行版本的peakfit.m 针对matlab或Octave。还有一个按键操作交互版本的交错ipf.m但仅供matlab。作为你自己的程序的一个元素用于自动拟合大量的信号，peakfit.m是比较好的选择。而ipf.m在探索一些信号的最佳拟合范围、峰形、峰的数量、基线校正模式等比较突出。这两个函数都为任何没有指定输入的参数提供了默认值，从而简化了操作。例如，起始值，如果没有指定输入参数，则程序会根据数据的长度和x轴的间隔来估计。相比前面提到的fitshape.m函数，peakfit.m函数有更多内置的峰形，不需要（虽然也可以给）初始为每个组分猜测位置和宽度，他具有背景校正功能以及其他提高质量和可靠性拟合的功能。


这些函数的最新版本可以通过使用引导样本方法估计预测标准差和峰参数的四分位差。看这个独立演示函数DemoPeakfitBootstrap  http://terpconnect.umd.edu/~toh/spectrum/DemoPeakfitBootstrap.m

---------------------------------------------------

peakfit的部分，我觉得应该和我毕设相关。

我目前需要改改我的声韵切分代码，再调整一下看看会不会用peakfit。

原文后面还有一些甚么样例，里面有关于函数调用的一些参数设置，我就给出加黑加粗的标题。

原文里面关于具体参数位置的会加黑加粗。

（峰形选择-峰的数目-峰宽约束-固定宽度形状-背景校正啊-信号中随机噪声啊）。

--原文资源很多，鼠标右键复制链接就可以获得哦。

---宝宝毕设垂死挣扎中RP 涨涨涨--