python中的Mann-Kendall单调趋势检验--及原理说明_liucheng_zimozigreat的博客-CSDN博客_mann-kendall python

前提假设：

当没有趋势时，随时间获得的数据是独立同分布的。独立的假设是说数据随着时间不是连续相关的。
所获得的时间序列上的数据代表了采样时的真实条件。（样本具有代表性）
样本的采集、处理和测量方法提供了总体样本中的无偏且具有代表性的观测值。

pymannkendall的Python项目

什么是mann-kendall检验？

mann-kendall趋势检验（有时称为mk检验）用于分析时间序列数据的一致性增加或减少趋势（单调趋势）。这是一个非参数检验，这意味着它适用于所有分布（即数据不必满足正态性假设），但数据应该没有序列相关性。如果数据具有序列相关性，则可能在显著水平上影响（p值）。这可能会导致误解。为了克服这一问题，研究者提出了几种修正的mann-kendall检验（hamed和rao修正的mk检验、yue和wang修正的mk检验、预白化法修正的mk检验等）。季节性mann-kendall检验也被用来消除季节性的影响。

mann-kendall检验是一种强大的趋势检验，因此针对空间条件，发展了多元mk检验、区域mk检验、相关mk检验、部分mk检验等修正的mann-kendall检验。pymannkendal是非参数mann-kendall趋势分析的纯python实现，它集合了几乎所有类型的mann-kendall测试。目前，该软件包有11个mann-kendall检验和2个sen斜率估计函数。功能简介如下：

原始mann-kendall检验（原始_检验）：原始mann-kendall检验是非参数检验，不考虑序列相关性或季节性影响。
hamed和rao修正的mk检验（hamed和rao修正的mk检验）：这个修正的mk检验由hamed和rao（1998）提出的解决序列自相关问题的方法。他们建议采用方差校正方法来改进趋势分析。用户可以通过在该函数中插入滞后数来考虑前n个显著滞后。默认情况下，它会考虑所有重要的延迟。
Yue和Wang修正的MK检验（Yue-Wang_修正的检验）：这也是Yue，S.，&Wang，C.Y.（2004）提出的考虑序列自相关的方差修正方法。用户还可以为计算设置所需的有效n滞后。
使用预白化方法的修正mk检验（预白化方法的修正）：Yue和Wang（2002）建议在应用趋势检验之前使用预白化时间序列的检验。
使用无趋势预白化方法的修正mk试验（无趋势预白化试验）：Yue和Wang（2002）也提出了在应用趋势试验之前去除趋势成分，然后对时间序列进行预白化的试验。
多变量mk检验（多变量检验）：这是hirsch（1982）提出的多参数mk检验。他用这种方法进行季节性mk检验，把每个月作为一个参数。
季节性MK检验（季节性检验）：对于季节性时间序列数据，Hirsch，R.M.，Slack，J.R.和Smith，R.A.（1982）提出了这个检验来计算季节性趋势。
区域mk检验（regional mk test）：基于Hirsch（1982）提出的季节性mk检验，Helsel，D.R.和Frans，L.M.，（2006）建议采用区域mk检验来计算区域尺度的总体趋势。
相关多变量mk检验（相关多变量检验）：hipel（1994）提出的参数相关的多变量mk检验。
相关季节性MK检验（相关季节性检验）：当时间序列与前一个或多个月/季节显著相关时，使用Hipel（1994）提出的方法。
部分mk检验（部分_检验）：在实际事件中，许多因素都会影响研究的主要响应参数，从而使趋势结果产生偏差。为了克服这个问题，libiseller（2002）提出了部分mk检验。它需要两个参数作为输入，一个是响应参数，另一个是独立参数。
泰尔-森斜率估计器（sen s-slope）：泰尔（1950）和森（1968）提出的估计单调趋势幅度的方法。
季节sen斜率估计量（季节sen斜率）：hipel（1994）提出的当数据具有季节性影响时估计单调趋势大小的方法。

功能详细信息：

所有mann-kendall检验函数的输入参数几乎相同。这些是：

x：向量（列表、numpy数组或pandas系列）数据
α：显著性水平（默认为0.05）
滞后：第一个有效滞后数（仅在hamed_rao_modification_test和yue_wang_modification_test中可用）
周期：季节性周期。月数据为12，周数据为52（仅在季节性测试中可用）

所有mann-kendall测试都返回一个命名元组，其中包含：

趋势：显示趋势（增加、减少或无趋势）
h：真（如果趋势存在）或假（如果趋势不存在）
p：显著性检验的p值
z：标准化测试统计
陶：肯德尔陶
s：Mann Kendal的分数
方差s：方差s
斜率：sen的斜率

sen的斜率函数需要数据向量。季节性sen的斜率也有可选的输入周期，默认值为12。两个sen的slope函数都只返回slope值。

Python pymannkendall包_程序模块 - PyPI - Python中文网

"""
Created on 05 March 2018
Update on 26 July 2019
@author: Md. Manjurul Hussain Shourov
version: 1.1
Approach: Vectorisation
Citation: Hussain et al., (2019). pyMannKendall: a python package for non parametric Mann Kendall family of trend tests.. Journal of Open Source Software, 4(39), 1556, https://doi.org/10.21105/joss.01556
"""from __future__ import division
import numpy as np
from scipy.stats import norm, rankdata
from collections import namedtuple# Supporting Functions
# Data Preprocessing
def __preprocessing(x):x = np.asarray(x)dim = x.ndimif dim == 1:c = 1elif dim == 2:(n, c) = x.shapeif c == 1:dim = 1x = x.flatten()else:print('Please check your dataset.')return x, c# Missing Values Analysis
def __missing_values_analysis(x, method = 'skip'):if method.lower() == 'skip':if x.ndim == 1:x = x[~np.isnan(x)]else:x = x[~np.isnan(x).any(axis=1)]n = len(x)return x, n# ACF Calculation
def __acf(x, nlags):y = x - x.mean()n = len(x)d = n * np.ones(2 * n - 1)acov = (np.correlate(y, y, 'full') / d)[n - 1:]return acov[:nlags+1]/acov[0]# vectorization approach to calculate mk score, S
def __mk_score(x, n):s = 0demo = np.ones(n) for k in range(n-1):s = s + np.sum(demo[k+1:n][x[k+1:n] > x[k]]) - np.sum(demo[k+1:n][x[k+1:n] < x[k]])return s# original Mann-Kendal's variance S calculation
def __variance_s(x, n):# calculate the unique dataunique_x = np.unique(x)g = len(unique_x)# calculate the var(s)if n == g:            # there is no tievar_s = (n*(n-1)*(2*n+5))/18else:                 # there are some ties in datatp = np.zeros(unique_x.shape)demo = np.ones(n)for i in range(g):tp[i] = np.sum(demo[x == unique_x[i]])var_s = (n*(n-1)*(2*n+5) - np.sum(tp*(tp-1)*(2*tp+5)))/18return var_s# standardized test statistic Z
def __z_score(s, var_s):if s > 0:z = (s - 1)/np.sqrt(var_s)elif s == 0:z = 0elif s < 0:z = (s + 1)/np.sqrt(var_s)return z# calculate the p_value
def __p_value(z, alpha):# two tail testp = 2*(1-norm.cdf(abs(z)))  h = abs(z) > norm.ppf(1-alpha/2)if (z < 0) and h:trend = 'decreasing'elif (z > 0) and h:trend = 'increasing'else:trend = 'no trend'return p, h, trenddef __R(x):n = len(x)R = []for j in range(n):i = np.arange(n)s = np.sum(np.sign(x[j] - x[i]))R.extend([(n + 1 + s)/2])return np.asarray(R)def __K(x,z):n = len(x)K = 0for i in range(n-1):j = np.arange(i,n)K = K + np.sum(np.sign((x[j] - x[i]) * (z[j] - z[i])))return K# Original Sens Estimator
def __sens_estimator(x):idx = 0n = len(x)d = np.ones(int(n*(n-1)/2))for i in range(n-1):j = np.arange(i+1,n)d[idx : idx + len(j)] = (x[j] - x[i]) / (j - i)idx = idx + len(j)return ddef sens_slope(x):"""This method proposed by Theil (1950) and Sen (1968) to estimate the magnitude of the monotonic trend.Input:x:   a one dimensional vector (list, numpy array or pandas series) dataOutput:slope: sen's slopeExamples-------->>> x = np.random.rand(120)>>> slope = sens_slope(x)"""x, c = __preprocessing(x)x, n = __missing_values_analysis(x, method = 'skip')return np.median(__sens_estimator(x))def seasonal_sens_slope(x, period=12):"""This method proposed by Hipel (1994) to estimate the magnitude of the monotonic trend, when data has seasonal effects.Input:x:   a vector (list, numpy array or pandas series) dataperiod: seasonal cycle. For monthly data it is 12, weekly data it is 52 (12 is the default)Output:slope: sen's slopeExamples-------->>> x = np.random.rand(120)>>> slope = seasonal_sens_slope(x, 12)"""x, c = __preprocessing(x)n = len(x)if x.ndim == 1:if np.mod(n,period) != 0:x = np.pad(x,(0,period - np.mod(n,period)), 'constant', constant_values=(np.nan,))x = x.reshape(int(len(x)/period),period)x, n = __missing_values_analysis(x, method = 'skip')d = []for i in range(period):d.extend(__sens_estimator(x[:,i]))return np.median(np.asarray(d))def original_test(x, alpha = 0.05):"""This function checks the Mann-Kendall (MK) test (Mann 1945, Kendall 1975, Gilbert 1987).Input:x: a vector (list, numpy array or pandas series) dataalpha: significance level (0.05 default)Output:trend: tells the trend (increasing, decreasing or no trend)h: True (if trend is present) or False (if trend is absence)p: p-value of the significance testz: normalized test statisticsTau: Kendall Taus: Mann-Kendal's scorevar_s: Variance Sslope: sen's slopeExamples-------->>> import pymannkendall as mk>>> x = np.random.rand(1000)>>> trend,h,p,z,tau,s,var_s,slope = mk.original_test(x,0.05)"""res = namedtuple('Mann_Kendall_Test', ['trend', 'h', 'p', 'z', 'Tau', 's', 'var_s', 'slope'])x, c = __preprocessing(x)x, n = __missing_values_analysis(x, method = 'skip')s = __mk_score(x, n)var_s = __variance_s(x, n)Tau = s/(.5*n*(n-1))z = __z_score(s, var_s)p, h, trend = __p_value(z, alpha)slope = sens_slope(x)return res(trend, h, p, z, Tau, s, var_s, slope)def hamed_rao_modification_test(x, alpha = 0.05, lag=None):"""This function checks the Modified Mann-Kendall (MK) test using Hamed and Rao (1998) method.Input:x: a vector (list, numpy array or pandas series) dataalpha: significance level (0.05 default)lag: No. of First Significant Lags (default None, You can use 3 for considering first 3 lags, which also proposed by Hamed and Rao(1998))Output:trend: tells the trend (increasing, decreasing or no trend)h: True (if trend is present) or False (if trend is absence)p: p-value of the significance testz: normalized test statisticsTau: Kendall Taus: Mann-Kendal's scorevar_s: Variance Sslope: sen's slopeExamples-------->>> import pymannkendall as mk>>> x = np.random.rand(1000)>>> trend,h,p,z,tau,s,var_s,slope = mk.hamed_rao_modification_test(x,0.05)"""res = namedtuple('Modified_Mann_Kendall_Test_Hamed_Rao_Approach', ['trend', 'h', 'p', 'z', 'Tau', 's', 'var_s', 'slope'])x, c = __preprocessing(x)x, n = __missing_values_analysis(x, method = 'skip')s = __mk_score(x, n)var_s = __variance_s(x, n)Tau = s/(.5*n*(n-1))# Hamed and Rao (1998) variance correctionif lag is None:lag = nelse:lag = lag + 1# detrending# x_detrend = x - np.multiply(range(1,n+1), np.median(x))slope = sens_slope(x)x_detrend = x - np.arange(1,n+1) * slopeI = rankdata(x_detrend)# account for autocorrelationacf_1 = __acf(I, nlags=lag-1)interval = norm.ppf(1 - alpha / 2) / np.sqrt(n)upper_bound = 0 + intervallower_bound = 0 - intervalsni = 0for i in range(1,lag):if (acf_1[i] <= upper_bound and acf_1[i] >= lower_bound):sni = snielse:sni += (n-i) * (n-i-1) * (n-i-2) * acf_1[i]n_ns = 1 + (2 / (n * (n-1) * (n-2))) * snivar_s = var_s * n_nsz = __z_score(s, var_s)p, h, trend = __p_value(z, alpha)return res(trend, h, p, z, Tau, s, var_s, slope)def yue_wang_modification_test(x, alpha = 0.05, lag=None):"""Input: This function checks the Modified Mann-Kendall (MK) test using Yue and Wang (2004) method.x: a vector (list, numpy array or pandas series) dataalpha: significance level (0.05 default)lag: No. of First Significant Lags (default None, You can use 1 for considering first 1 lags, which also proposed by Yue and Wang (2004))Output:trend: tells the trend (increasing, decreasing or no trend)h: True (if trend is present) or False (if trend is absence)p: p-value of the significance testz: normalized test statisticsTau: Kendall Taus: Mann-Kendal's scorevar_s: Variance Sslope: sen's slopeExamples-------->>> import pymannkendall as mk>>> x = np.random.rand(1000)>>> trend,h,p,z,tau,s,var_s,slope = mk.yue_wang_modification_test(x,0.05)"""res = namedtuple('Modified_Mann_Kendall_Test_Yue_Wang_Approach', ['trend', 'h', 'p', 'z', 'Tau', 's', 'var_s', 'slope'])x, c = __preprocessing(x)x, n = __missing_values_analysis(x, method = 'skip')s = __mk_score(x, n)var_s = __variance_s(x, n)Tau = s/(.5*n*(n-1))# Yue and Wang (2004) variance correctionif lag is None:lag = nelse:lag = lag + 1# detrendingslope = sens_slope(x)x_detrend = x - np.arange(1,n+1) * slope# account for autocorrelationacf_1 = __acf(x_detrend, nlags=lag-1)idx = np.arange(1,lag)sni = np.sum((1 - idx/n) * acf_1[idx])n_ns = 1 + 2 * snivar_s = var_s * n_nsz = __z_score(s, var_s)p, h, trend = __p_value(z, alpha)return res(trend, h, p, z, Tau, s, var_s, slope)def pre_whitening_modification_test(x, alpha = 0.05):"""This function checks the Modified Mann-Kendall (MK) test using Pre-Whitening method proposed by Yue and Wang (2002).Input:x: a vector (list, numpy array or pandas series) dataalpha: significance level (0.05 default)Output:trend: tells the trend (increasing, decreasing or no trend)h: True (if trend is present) or False (if trend is absence)p: p-value of the significance testz: normalized test statisticss: Mann-Kendal's scorevar_s: Variance Sslope: sen's slopeExamples-------->>> import pymannkendall as mk>>> x = np.random.rand(1000)>>> trend,h,p,z,tau,s,var_s,slope = mk.pre_whitening_modification_test(x,0.05)"""res = namedtuple('Modified_Mann_Kendall_Test_PreWhitening_Approach', ['trend', 'h', 'p', 'z', 'Tau', 's', 'var_s', 'slope'])x, c = __preprocessing(x)x, n = __missing_values_analysis(x, method = 'skip')# PreWhiteningacf_1 = __acf(x, nlags=1)[1]a = range(0, n-1)b = range(1, n)x = x[b] - x[a]*acf_1n = len(x)s = __mk_score(x, n)var_s = __variance_s(x, n)Tau = s/(.5*n*(n-1))z = __z_score(s, var_s)p, h, trend = __p_value(z, alpha)slope = sens_slope(x)return res(trend, h, p, z, Tau, s, var_s, slope)def trend_free_pre_whitening_modification_test(x, alpha = 0.05):"""This function checks the Modified Mann-Kendall (MK) test using the trend-free Pre-Whitening method proposed by Yue and Wang (2002).Input:x: a vector (list, numpy array or pandas series) dataalpha: significance level (0.05 default)Output:trend: tells the trend (increasing, decreasing or no trend)h: True (if trend is present) or False (if trend is absence)p: p-value of the significance testz: normalized test statisticss: Mann-Kendal's scorevar_s: Variance Sslope: sen's slopeExamples-------->>> import pymannkendall as mk>>> x = np.random.rand(1000)>>> trend,h,p,z,tau,s,var_s,slope = mk.trend_free_pre_whitening_modification_test(x,0.05)"""res = namedtuple('Modified_Mann_Kendall_Test_Trend_Free_PreWhitening_Approach', ['trend', 'h', 'p', 'z', 'Tau', 's', 'var_s', 'slope'])x, c = __preprocessing(x)x, n = __missing_values_analysis(x, method = 'skip')# detrendingslope = sens_slope(x)x_detrend = x - np.arange(1,n+1) * slope# PreWhiteningacf_1 = __acf(x_detrend, nlags=1)[1]a = range(0, n-1)b = range(1, n)x = x_detrend[b] - x_detrend[a]*acf_1n = len(x)x = x + np.arange(1,n+1) * slopes = __mk_score(x, n)var_s = __variance_s(x, n)Tau = s/(.5*n*(n-1))z = __z_score(s, var_s)p, h, trend = __p_value(z, alpha)slope = sens_slope(x)return res(trend, h, p, z, Tau, s, var_s, slope)def multivariate_test(x, alpha = 0.05):"""This function checks the Multivariate Mann-Kendall (MK) test, which is originally proposed by R. M. Hirsch and J. R. Slack (1984) for the seasonal Mann-Kendall test. Later this method also used Helsel (2006) for Regional Mann-Kendall test.Input:x: a matrix of dataalpha: significance level (0.05 default)Output:trend: tells the trend (increasing, decreasing or no trend)h: True (if trend is present) or False (if trend is absence)p: p-value of the significance testz: normalized test statisticsTau: Kendall Taus: Mann-Kendal's scorevar_s: Variance Sslope: sen's slopeExamples-------->>> import pymannkendall as mk>>> x = np.random.rand(1000)>>> trend,h,p,z,tau,s,var_s,slope = mk.multivariate_test(x,0.05)"""res = namedtuple('Multivariate_Mann_Kendall_Test', ['trend', 'h', 'p', 'z', 'Tau', 's', 'var_s', 'slope'])s = 0var_s = 0denom = 0x, c = __preprocessing(x)
#     x, n = __missing_values_analysis(x, method = 'skip')  # It makes all column at the same sizefor i in range(c):if c == 1:x_new, n = __missing_values_analysis(x, method = 'skip')  # It makes all column at deferent sizeelse:x_new, n = __missing_values_analysis(x[:,i], method = 'skip')  # It makes all column at deferent sizes = s + __mk_score(x_new, n)var_s = var_s + __variance_s(x_new, n)denom = denom + (.5*n*(n-1))Tau = s/denomz = __z_score(s, var_s)p, h, trend = __p_value(z, alpha)slope = seasonal_sens_slope(x, period = c)return res(trend, h, p, z, Tau, s, var_s, slope)def seasonal_test(x, period = 12, alpha = 0.05):"""This function checks the  Seasonal Mann-Kendall (MK) test (Hirsch, R. M., Slack, J. R. 1984).Input:x:   a vector of dataperiod: seasonal cycle. For monthly data it is 12, weekly data it is 52 (12 is the default)alpha: significance level (0.05 is the default)Output:trend: tells the trend (increasing, decreasing or no trend)h: True (if trend is present) or False (if trend is absence)p: p-value of the significance testz: normalized test statisticsTau: Kendall Taus: Mann-Kendal's scorevar_s: Variance Sslope: sen's slopeExamples-------->>> import pymannkendall as mk>>> x = np.random.rand(1000)>>> trend,h,p,z,tau,s,var_s,slope = mk.seasonal_test(x,0.05)"""res = namedtuple('Seasonal_Mann_Kendall_Test', ['trend', 'h', 'p', 'z', 'Tau', 's', 'var_s', 'slope'])x, c = __preprocessing(x)n = len(x)if x.ndim == 1:if np.mod(n,period) != 0:x = np.pad(x,(0,period - np.mod(n,period)), 'constant', constant_values=(np.nan,))x = x.reshape(int(len(x)/period),period)trend, h, p, z, Tau, s, var_s, slope = multivariate_test(x, alpha = alpha)return res(trend, h, p, z, Tau, s, var_s, slope)def regional_test(x, alpha = 0.05):"""This function checks the Regional Mann-Kendall (MK) test (Helsel 2006).Input:x:   a matrix of dataalpha: significance level (0.05 default)Output:trend: tells the trend (increasing, decreasing or no trend)h: True (if trend is present) or False (if trend is absence)p: p-value of the significance testz: normalized test statisticsTau: Kendall Taus: Mann-Kendal's scorevar_s: Variance Sslope: sen's slopeExamples-------->>> import pymannkendall as mk>>> x = np.random.rand(1000)>>> trend,h,p,z,tau,s,var_s,slope = mk.regional_test(x,0.05)"""res = namedtuple('Regional_Mann_Kendall_Test', ['trend', 'h', 'p', 'z', 'Tau', 's', 'var_s', 'slope'])trend, h, p, z, Tau, s, var_s, slope = multivariate_test(x)return res(trend, h, p, z, Tau, s, var_s, slope)def correlated_multivariate_test(x, alpha = 0.05):"""This function checks the Correlated Multivariate Mann-Kendall (MK) test (Libiseller and Grimvall (2002)).Input:x:   a matrix of dataalpha: significance level (0.05 default)Output:trend: tells the trend (increasing, decreasing or no trend)h: True (if trend is present) or False (if trend is absence)p: p-value of the significance testz: normalized test statisticsTau: Kendall Taus: Mann-Kendal's scorevar_s: Variance Sslope: sen's slopeExamples-------->>> import pymannkendall as mk>>> x = np.random.rand(1000)>>> trend,h,p,z,tau,s,var_s,slope = mk.correlated_multivariate_test(x,0.05)"""res = namedtuple('Correlated_Multivariate_Mann_Kendall_Test', ['trend', 'h', 'p', 'z', 'Tau', 's', 'var_s', 'slope'])x, c = __preprocessing(x)x, n = __missing_values_analysis(x, method = 'skip')s = 0denom = 0for i in range(c):s = s + __mk_score(x[:,i], n)denom = denom + (.5*n*(n-1))Tau = s/denomGamma = np.ones([c,c])for i in range(1,c):for j in range(i):k = __K(x[:,i], x[:,j])ri = __R(x[:,i])rj = __R(x[:,j])Gamma[i,j] = (k + 4 * np.sum(ri * rj) - n*(n+1)**2)/3Gamma[j,i] = Gamma[i,j]for i in range(c):k = __K(x[:,i], x[:,i])ri = __R(x[:,i])rj = __R(x[:,i])Gamma[i,i] = (k + 4 * np.sum(ri * rj) - n*(n+1)**2)/3var_s = np.sum(Gamma)z = s / np.sqrt(var_s)p, h, trend = __p_value(z, alpha)slope = seasonal_sens_slope(x, period=c)return res(trend, h, p, z, Tau, s, var_s, slope)def correlated_seasonal_test(x, period = 12 ,alpha = 0.05):"""This function checks the Correlated Seasonal Mann-Kendall (MK) test (Hipel [1994] ).Input:x:   a matrix of dataperiod: seasonal cycle. For monthly data it is 12, weekly data it is 52 (12 is default)alpha: significance level (0.05 default)Output:trend: tells the trend (increasing, decreasing or no trend)h: True (if trend is present) or False (if trend is absence)p: p-value of the significance testz: normalized test statisticsTau: Kendall Taus: Mann-Kendal's scorevar_s: Variance Sslope: sen's slopeExamples-------->>> import pymannkendall as mk>>> x = np.random.rand(1000)>>> trend,h,p,z,tau,s,var_s,slope = mk.correlated_seasonal_test(x,0.05)"""res = namedtuple('Correlated_Seasonal_Mann_Kendall_test', ['trend', 'h', 'p', 'z', 'Tau', 's', 'var_s', 'slope'])x, c = __preprocessing(x)n = len(x)if x.ndim == 1:if np.mod(n,period) != 0:x = np.pad(x,(0,period - np.mod(n,period)), 'constant', constant_values=(np.nan,))x = x.reshape(int(len(x)/period),period)trend, h, p, z, Tau, s, var_s, slope = correlated_multivariate_test(x)return res(trend, h, p, z, Tau, s, var_s, slope)def partial_test(x, alpha = 0.05):"""This function checks the Partial Mann-Kendall (MK) test (Libiseller and Grimvall (2002)).Input:x: a matrix with 2 columnsalpha: significance level (0.05 default)Output:trend: tells the trend (increasing, decreasing or no trend)h: True (if trend is present) or False (if trend is absence)p: p-value of the significance testz: normalized test statisticsTau: Kendall Taus: Mann-Kendal's scorevar_s: Variance Sslope: sen's slopeExamples-------->>> import pymannkendall as mk>>> x = np.random.rand(1000)>>> trend,h,p,z,tau,s,var_s,slope = mk.partial_test(x,0.05)"""res = namedtuple('Partial_Mann_Kendall_Test', ['trend', 'h', 'p', 'z', 'Tau', 's', 'var_s', 'slope'])x_old, c = __preprocessing(x)x_old, n = __missing_values_analysis(x_old, method = 'skip')if c != 2:raise ValueError('Partial Mann Kendall test required two parameters/columns. Here column no ' + str(c) + ' is not equal to 2.')x = x_old[:,0]y = x_old[:,1]x_score = __mk_score(x, n)y_score = __mk_score(y, n)k = __K(x, y)rx = __R(x)ry = __R(y)sigma = (k + 4 * np.sum(rx * ry) - n*(n+1)**2)/3rho = sigma / (n*(n-1)*(2*n+5)/18)s = x_score - rho * y_scorevar_s = (1 - rho**2) * (n*(n-1)*(2*n+5))/18Tau = x_score/(.5*n*(n-1))z = s / np.sqrt(var_s)p, h, trend = __p_value(z, alpha)slope = sens_slope(x)return res(trend, h, p, z, Tau, s, var_s, slope)

批量逐点检验（未处理自相关）

scipy.stats.kendalltau（）函数

Kendall's tau-b（肯德尔）等级相关系数：用于反映分类变量相关性的指标，适用于两个分类变量（时间—水文要素）均为有序分类的情况。对相关的有序变量进行非参数相关检验；取值范围在-1-1之间，此检验适合于正方形表格；

scipy.stats.kendalltau — SciPy v0.19.1 Reference Guide

from scipy import stats
import pandas as pd
import numpy as npdata = pd.read_csv(r"C:\Users\Leon\Desktop\Pre.csv")#print (data)###38行*994列（38年994个cell）
x = range(38)
print (x)
y = np.zeros((0))
for j in range(994):b = stats.kendalltau(x,data.values[:,j]) ##MK检验，结果包含两个参数：tau, p_value y = np.append(y, b, axis=0)print(b)
print(type(y))
#np.savetxt("C:/Users/Leon/Desktop/P.txt",y) ##保存ndarray类型数据

稳健回归（Robustness regression）

最小二乘法的弊端

之前文章里的关于线性回归的模型，都是基于最小二乘法来实现的。但是，当数据样本点出现很多的异常点（outliers），这些异常点对回归模型的影响会非常的大，传统的基于最小二乘的回归方法将不适用。

比如下图中所示，数据中存在一个异常点，如果不剔除改点，适用OLS方法来做回归的话，那么就会得到途中红色的那条线；如果将这个异常点剔除掉的话，那么就可以得到图中蓝色的那条线。显然，蓝色的线比红色的线对数据有更强的解释性，这就是OLS在做回归分析时候的弊端。

当然，可以考虑在做回归分析之前，对数据做预处理，剔除掉那些异常点。但是，在实际的数据中，存在两个问题：

异常点并不能很好的确定，并没有一个很好的标准用于确定哪些点是异常点
即便确定了异常点，但这些被确定为异常的点，真的是错误的数据吗？很有可能这看似异常的点，就是原始模型的数据，如果是这样的话，那么这些异常的点就会带有大量的原始模型的信息，剔除之后就会丢失大量的信息。
再比如下面这幅图，其中红色的都是异常点，但是很难从数据中剔除出去。

稳健回归

稳健回归（Robust regression），就是当最小二乘法遇到上述的，数据样本点存在异常点的时候，用于代替最小二乘法的一个算法。当然，稳健回归还可以用于异常点检测，或者是找出那些对模型影响最大的样本点。

Breakdown point

关于稳健回归，有一个名词需要做解释：Breakdown point，这个名词我并不想翻译，我也没找到一个很好的中文翻译。对于一个估计器而言，原始数据中混入了脏数据，那么，Breakdown point 指的就是在这个估计器给出错误的模型估计之前，脏数据最大的比例 αα，Breakdown point 代表的是一个估计器对脏数据的最大容忍度。

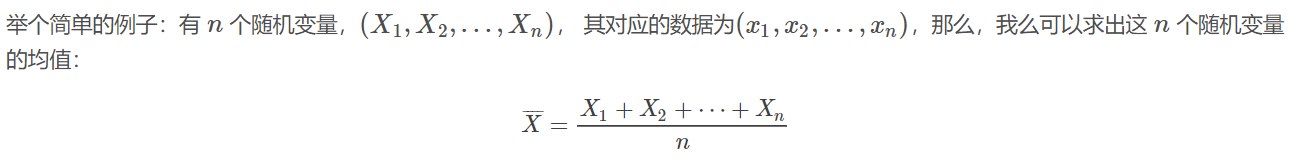
这个均值估计器的Breakdown point 为0，因为使任意一个xixi变成足够大的脏数据之后，上面估计出来的均值，就不再正确了。

毫无疑问，Breakdown point越大，估计器就越稳健。

Breakdown point 是不可能达到 50% 的，因为如果总体样本中超过一半的数据是脏数据了，那么从统计上来说，就无法将样本中的隐藏分布和脏数据的分布给区分开来。

本文主要介绍两种稳健回归模型：RANSAC（RANdom SAmple Consensus 随机采样一致性）和Theil-Sen estimator。

RANSAC随机采样一致性算法

RANSAC算法的输入是一组观测数据（往往含有较大的噪声或无效点），它是一种重采样技术（resampling technique），通过估计模型参数所需的最小的样本点数，来得到备选模型集合，然后在不断的对集合进行扩充，其算法步骤为：

RANSAC算法是从输入样本集合的内点的随机子集中学习模型。

RANSAC算法是一个非确定性算法（non-deterministic algorithm），这个算法只能得以一定的概率得到一个还不错的结果，在基本模型已定的情况下，结果的好坏程度主要取决于算法最大的迭代次数。

RANSAC算法在线性和非线性回归中都得到了广泛的应用，而其最典型也是最成功的应用，莫过于在图像处理中处理图像拼接问题，这部分在Opencv中有相关的实现。

从总体上来讲，RANSAC算法将输入样本分成了两个大的子集：内点（inliers）和外点（outliers）。其中内点的数据分布会受到噪声的影响；而外点主要来自于错误的测量手段或者是对数据错误的假设。而RANSAC算法最终的结果是基于算法所确定的内点集合得到的。

下面这份代码是RANSAC的适用实例：

# -*- coding: utf-8 -*-"""
author : duanxxnj@163.com
time : 2016-07-07-15-36"""import numpy as np
import time
from sklearn import linear_model,datasetsimport matplotlib.pyplot as plt# 产生数据样本点集合
# 样本点的特征X维度为1维，输出y的维度也为1维
# 输出是在输入的基础上加入了高斯噪声N（0,10）
# 产生的样本点数目为1000个n_samples = 1000
X, y, coef = datasets.make_regression(n_samples=n_samples,n_features=1,n_informative=1,noise=10,coef=True,random_state=0)# 将上面产生的样本点中的前50个设为异常点（外点）
# 即：让前50个点偏离原来的位置，模拟错误的测量带来的误差
n_outliers = 50
np.random.seed(int(time.time()) % 100)
X[:n_outliers] = 3 + 0.5 * np.random.normal(size=(n_outliers, 1))
y[:n_outliers] = -3 + 0.5 * np.random.normal(size=n_outliers)# 用普通线性模型拟合X，y
model = linear_model.LinearRegression()
model.fit(X, y)# 使用RANSAC算法拟合X,y
model_ransac = linear_model.RANSACRegressor(linear_model.LinearRegression())
model_ransac.fit(X, y)
inlier_mask = model_ransac.inlier_mask_
outlier_mask = np.logical_not(inlier_mask)# 使用一般回归模型和RANSAC算法分别对测试数据做预测
line_X = np.arange(-5, 5)
line_y = model.predict(line_X[:, np.newaxis])
line_y_ransac = model_ransac.predict(line_X[:, np.newaxis])print "真实数据参数：", coef
print "线性回归模型参数：", model.coef_
print "RANSAC算法参数： ", model_ransac.estimator_.coef_plt.plot(X[inlier_mask], y[inlier_mask], '.g', label='Inliers')
plt.plot(X[outlier_mask], y[outlier_mask], '.r', label='Outliers')
plt.plot(line_X, line_y, '-k', label='Linear Regression')
plt.plot(line_X, line_y_ransac, '-b', label="RANSAC Regression")
plt.legend(loc='upper left')
plt.show()

figure_1-1.png-46.8kB

运行结果为：

真实数据参数： 82.1903908408
线性回归模型参数： [ 55.19291974]
RANSAC算法参数：  [ 82.08533159]

Theil-Sen Regression 泰尔森回归

Theil-Sen回归是一个参数中值估计器，它适用泛化中值，对多维数据进行估计，因此其对多维的异常点（outliers 外点）有很强的稳健性。

在实践中发现，随着数据特征维度的提升，Theil-Sen回归的效果不断的下降，在高维数据中，Theil-Sen回归的效果有时甚至还不如OLS（最小二乘）。

在之间的文章《线性回归》中讨论过，OLS方法是渐进无偏的，Theil-Sen方法在渐进无偏方面和OLS性能相似。和OLS方法不同的是，Theil-Sen方法是一种非参数方法，其对数据的潜在分布不做任何的假设。Theil-Sen方法是一种基于中值的估计其，所以其对异常点有更强的稳健性。

在单变量回归问题中，Theil-Sen方法的Breakdown point为29.3%，也就是说，Theil-Sen方法可以容忍29.3%的数据是outliers。

# -*- coding: utf-8 -*-"""@author : duanxxnj@163.com
@time ；2016-07-08_08-50Theil-Sen 回归本例生成一个数据集，然后在该数据集上测试Theil-Sen回归"""print __doc__import time
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression, TheilSenRegressor,\RANSACRegressorestimators = [('OLS', LinearRegression()),('Theil-Sen', TheilSenRegressor())]# 异常值仅仅出现在y轴
np.random.seed((int)(time.time() % 100))
n_samples = 200# 线性模型的函数形式为： y = 3 * x + N(2, .1 ** 2)
x = np.random.randn(n_samples)
w = 3.
c = 2.
noise = c + 0.1 * np.random.randn(n_samples)
y = w * x + noise# 加入10%的异常值,最后20个值称为异常值
y[-20:] += -20 * x[-20:]X = x[:, np.newaxis]
plt.plot(X, y, 'k+', mew=2, ms=8)
line_x = np.array([-3, 3])for name, estimator in estimators:t0 = time.time()estimator.fit(X, y)elapsed_time = time.time() - t0y_pred = estimator.predict(line_x.reshape(2, 1))plt.plot(line_x, y_pred, label='%s (fit time: %.2fs)'%(name, elapsed_time))plt.axis('tight')
plt.legend(loc='upper left')plt.show()

figure_1-1.png-32.2kB