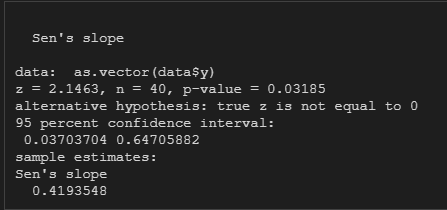
正态分布方法判别,独立样本T检验及Mann-Whitney U 检验操作
- 正态性校验
- 数据整体是否符合正态分布
- SPSS中的操作步骤
- 某分组上是否符合正态分布
- SPSS中的操作步骤
- 独立样本t检验
- SPSS中的操作步骤
- Mann-Whitney U 检验
- SPSS中的操作步骤
- 方法1
- 操作步骤
- 方法2
- 操作步骤
- 计算各分组的中位数
- 结果解读
一个连续型变量数据是否符合正态分布,通常有以下两种情况:一种情况是数据本身整体的分布是否符合正态分布;另一种就是数据在某个分组上是否符合正态分布。
正态性校验
数据整体是否符合正态分布
检验数据本身整体是否符合正态分布
下面是为了分析菌群α多样性指数Chao1,Shannon以及observed_otus指数在正常和模型组之间有无显著性差异,所以需要先分析Shannon这一列数据是否符合正态分布(图1)
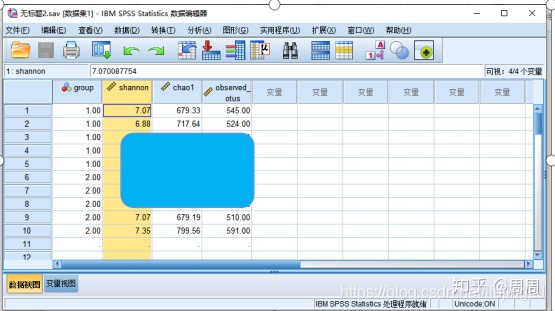
SPSS中的操作步骤
①依次点击:“分析”-“非参数检验”-“旧对话框”-“单样本K-S”(图2),在弹出的对话框中,将“年龄”选入右侧栏中,并在下方“检验分布”中勾选“正态”(图3)选项。然后点击确定。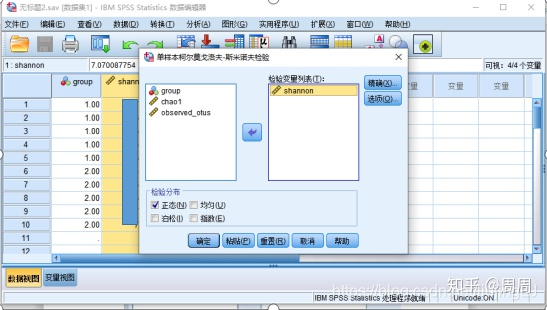
②分析结果
从上方SPSS的输出结果可以看出:渐近显著性(双侧)为0.073大于0.05,意味着Shannon数据整体是符合正态分布的。
检验变量在某个分组上是否符合正态分布

还是用上面的案例,如果要比较不同组别的Shannon是否有差异,这时候就需要检验Shannon在不同组别上是否符合正态分布。
某分组上是否符合正态分布
在SPSS中,正态分布的检验方法有:计算偏度系数(Skewness)和峰度系数(Kurtosis)、Kolmogorov-Smirnov检验(KS检验或D检验)、Shapiro-Wilk(SW检验或W检验)、直方图、QQ图等。
SPSS中的操作步骤
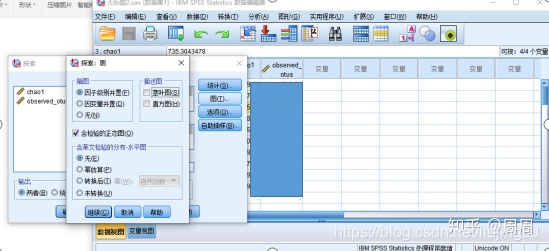
①依次点击:“分析”-“描述统计”-“探索”

②在弹出的窗口中,将“Shannon”选入因变量列表,将“性别”选入“Group”列表

③设置参数,点击右侧的“图”按钮,勾选“含检验的正态图”,点击继续,再点击确定。
④结果分析,在结果界面点击左侧“正态性检验”标签,在右侧的正态性检验表中,看夏皮洛-威尔克那部分的显著性水平
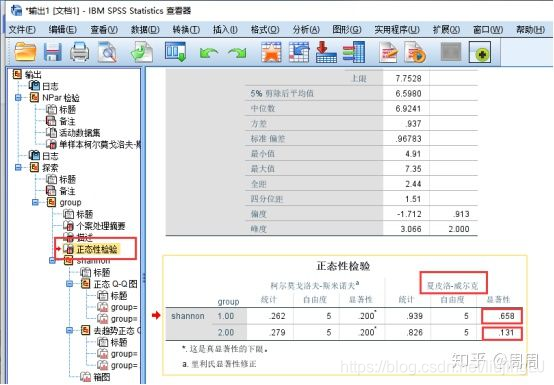
此表,是对数据的统计描述,我们可以关注下偏度(Skewness)和峰度(Kurtosis)。
偏度SK越趋近0,数据越服从正态分布,众数=中位数=平均数;SK>0,为正偏态或左偏,众数<中位数<平均数;SK<0,为负偏态或右偏,众数>中位数>平均数。
峰度KG越趋近3,数据越服从正态分布;KG>3,峰度尖锐;KG<3,峰度扁平。(或exceess_KG=KG-3,exceess_KG越趋近0,数据越服从正态分布)
但是仅根据偏度和峰度还不足以判断数据是否服从正态分布,需要做进一步的检验。
由上图正态性校验可以看出1分组P>0.05,2分组P>0.05,**这里注意了:当所有分组的P都大于0.05,就能说是符合正态分布,只要有一个分组的P小于0.05,就拒绝变量符合正态分布的结论。**Shannon在分组上就符合正态分布了,所以就可以使用参数类的t检验,若不符合就使用非参数Mann-Whitney检验了。
注意:大样本看KS,小样本看SW。
独立样本t检验
SPSS中的操作步骤
①点击“分析”–“比较平均值”–“独立样本t检验”
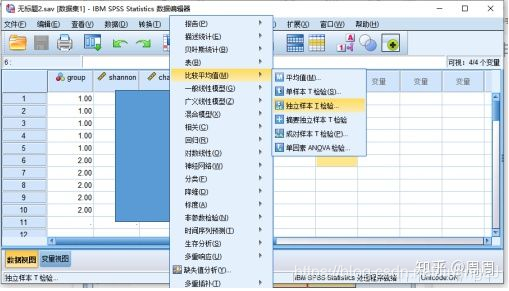
②将Shannon选入右侧检验变量,将Group选入分组变量
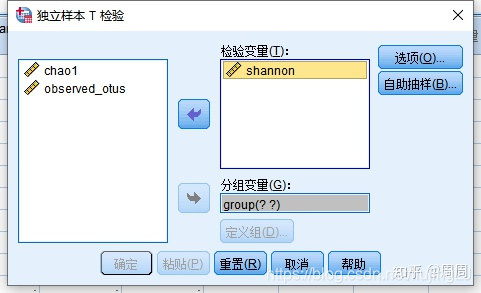
③点击“定义组”,设置性别的分组编码,然后点击确定进行运算
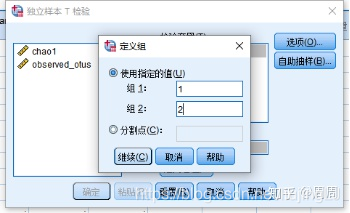
④结果分析

基于来莱文方差等同性检验,如果方差齐,就选择第一行的T检验结果,如果方差不齐则接受第二行的T检验结果。这里判定方差齐性的标准为莱文方差等同性检验的显著性,基于本例为0.107>0.05,意味着原假设方差齐成立,接受假设方差齐。因此这里的T检验结果为:T=0.499,P=0.631>0.05。所以Shannon指数在正常与模型组之间没有显著性差异。
Mann-Whitney U 检验
Mann-Whitney U 检验是用得最广泛的两独立样本秩和检验方法。简单的说,该检验是与独立样本t检验相对应的方法,当正态分布、方差齐性等不能达到t检验的要求时,可以使用该检验。其假设基础是:若两个样本有差异,则他们的中心位置将不同。
为了分析菌群α多样性指数Chao1,Shannon以及observed_otus指数在正常和模型组之间有无显著性差异。
SPSS数据视图:
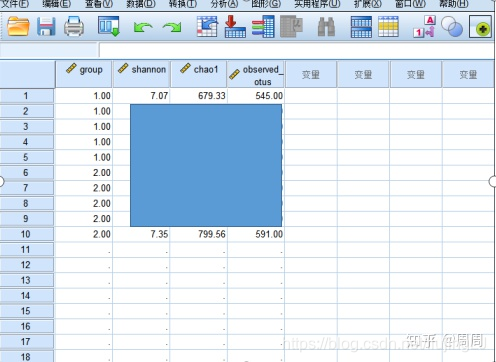
变量视图:

SPSS中的操作步骤
方法1
U值计算公式:U=n1*n2+n1(n1+1)/2-R
R为R1和R2中较小的值
R1、R2分别为两组秩的总和
操作步骤
进入菜单如下图:
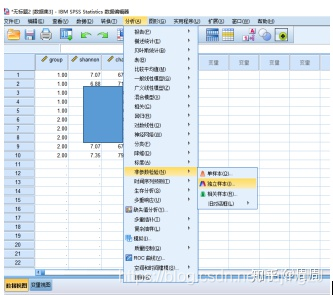
点击进入如下的界面,“目标”选项卡定制分析
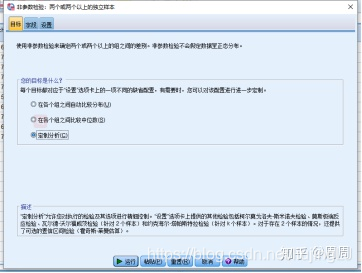
进入“字段”选项卡,将“Group”选入“检验字段”框,将“Chao1,Shannon和Observe-otus”选入“检验字段”框中。

再进入“设置”选项卡,选中“定制检验”单选按钮,选择“Mann-Whitney U(二样本)”检验。点击“运行”即可。
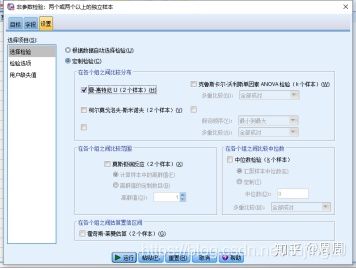
结果解读
这是输出的主要结果,零假设是“在Group类别上,Shannon等分布相同”,其P=0.690,0.548,0.421>0.05,故保留原假设,认为这三个指数在正常组与模型组之间没有统计学差异。
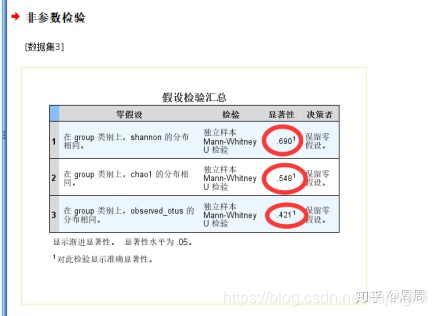
双击该数据集,可以查看详细信息。
方法2
U值计算公式:
U1=n1n2+n1(n1+1)/2-R1
U2=n1n2+n2(n2+1)/2-R2
U为U1和U2中较小的值
操作步骤
- 在SPSS 18及之后版本中,可以点击Analyze — Nonparametric Tests — Legacy Dialogs(旧对话框) — 2 Independent Samples(如下图所示),本文按照此操作步骤为例来展示。[版本18之前的软件点击Analyze——Nonparametric Tests——2 Independent Samples]

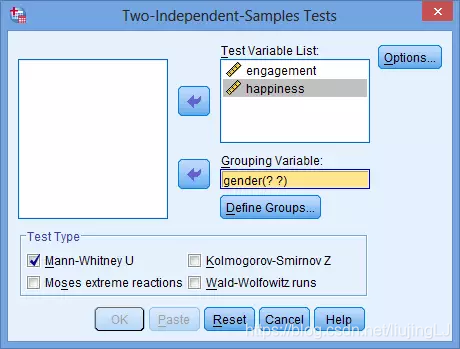
出现如下对话框,勾选检验类型“Test Type”中的“Mann-Whitney U”选项:
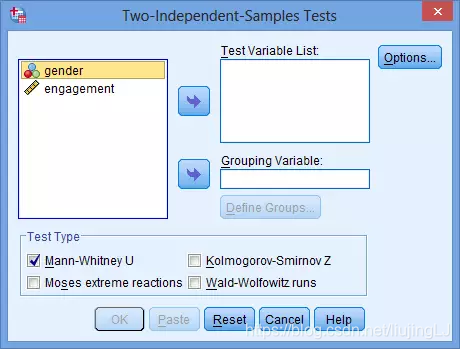
- 将因变量“engagement”放入“Test Variable List”,将自变量“gender”放入“Grouping Variable”
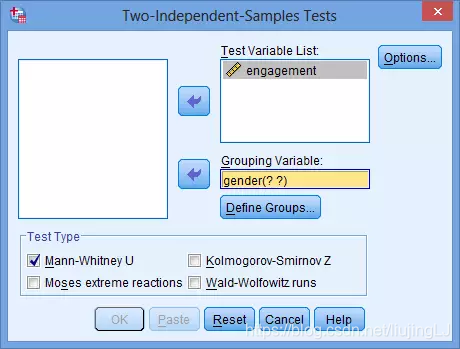
注:如果有多个需要分析的因变量,可以一齐放入“Test Variable List”,在报告结果时可以同时显示多个因变量与性别之间的关系。例如,加入自变量“happiness” (如下图所示):
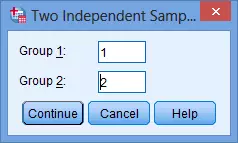
- 点击分组变量中的分组定义“Define Groups”,将性别分组中男性组的赋值1填写至“Group 1”,将女性组的赋值2填写至“Group 2”,点击下方的“Continue”。
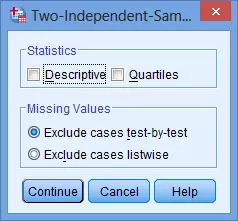
- 返回至主对话框后点击“Option”按钮,如果在处理的数据中有缺失值,在“Missing Values”中选择“Exclude cases test-by-test”,在进行Mann-Whitney U检验时可以自动排除缺失数据。
注:如果选择了多个因变量进入此项分析,例如数据中有两个因变量:
“engagement”与“happiness”,这两个因变量中均有缺失值,第8名调查者的“engagement”数据缺失,第11名调查者的“happiness”数据缺失,处理缺失数据时选择“Exclude cases test-by-test”或者“Exclude cases listwise”是有区别的:
① 选择“Exclude cases test-by-test”
选择“Exclude cases test-by-test”后,只排除缺失的数据,其余数据均保留。如分析“engagement”时,只排除第8名调查者的缺失数据,而第11名调查者的数据保留,而分析“happiness”时只排除第11名调查者的缺失数据,而第8名调查者的数据保留。
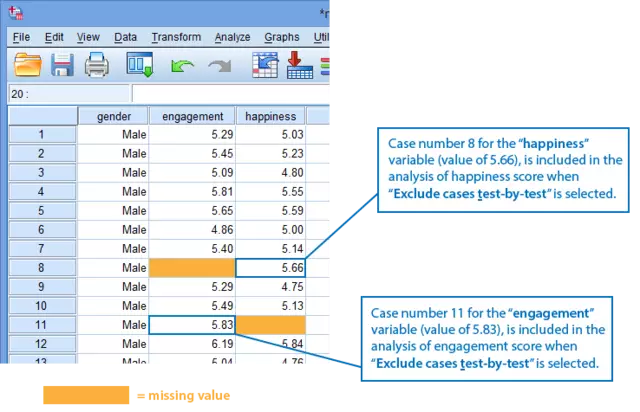
【选择“Exclude cases test-by-test”模式,分析幸福值的性别差异时将包括第8名调查者的“happiness”变量值(5.66);选择“Exclude cases test-by-test”模式,分析接受程度评分的性别差异时将包括第11名调查者的“engagement”变量值(5.83)】
② 选择“Exclude cases listwise”
选择“Exclude cases listwise”意味着,任何一个因变量中有数据缺失,那么该调查者的全部数据都被剔除,例如第8名调查者中“engagement”中数据缺失,第11名调查者“happiness”数据缺失,那么在在进行Mann-Whitney U检验时将第8名与第11名调查者的数据同时剔除。
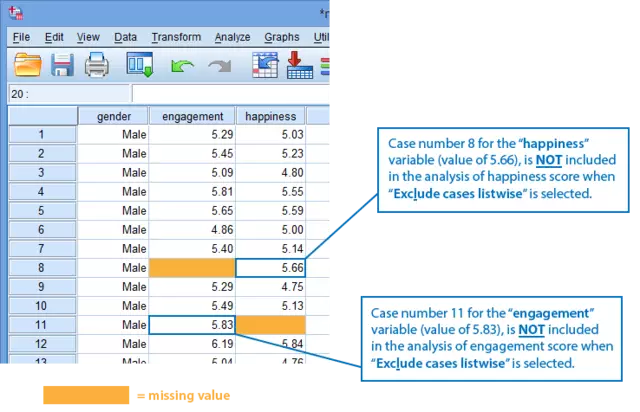
【选择“Exclude cases listwise”模式,分析幸福值的性别差异时将不包括第8名调查者的“happiness”变量值(5.66);选择“Exclude cases listwise”模式,分析接受程度评分的性别差异时将不包括第11名调查者的“engagement”变量值(5.83)】
-
选择对话框中Statistics中的Deive与Quartiles选项后选择Continue。
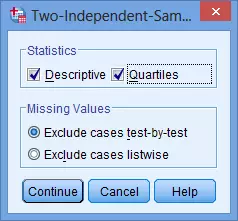
提示:选择Statistics中的Deive与Quartiles选项后,报告出的结果并不一定是有用的,例如我们希望分别得到男性和女性组中广告接受程度的中位数,而结果只会报告广告接受程度及性别变量的中位数。因此,下一步我们介绍两组的中位数如何计算。 -
最后回到Two-Independent-Sample Tests对话框,点击OK,得到输出结果。
计算各分组的中位数
在SPSS软件中进行Mann-Whitney U检验,无法报告各分组的中位数,而中位数是两组比较时的重要参数。因此,我们可以通过以下6步完成中位数的计算。
(1) 点击菜单中Analyze>Compare Means>Means…
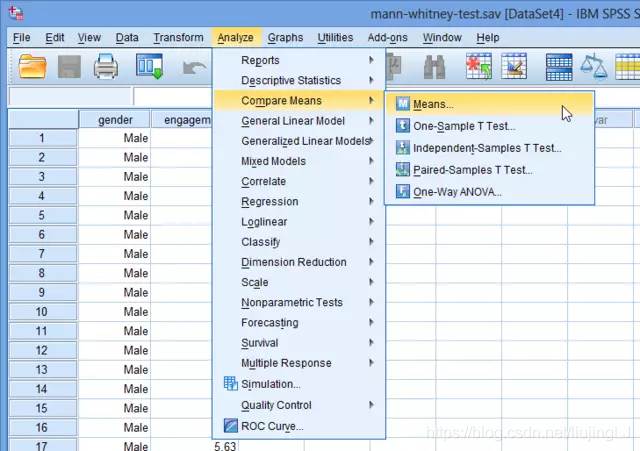
出现中位数计算的对话框,如下图所示:
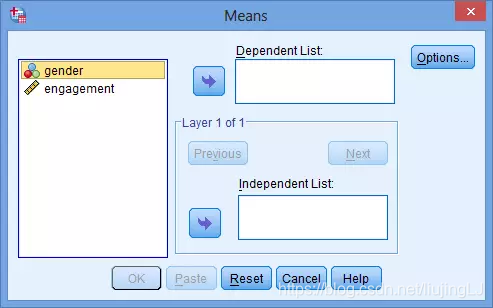
2. 将engagement放入因变量列表中,将gender放入自变量中。
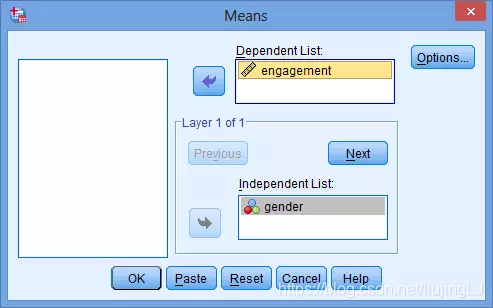
3. 选择Options按钮,选择需要计算的参数:

4. 选择Median,取消预先选择的Mean、Number of Cases、Standard Deviation。
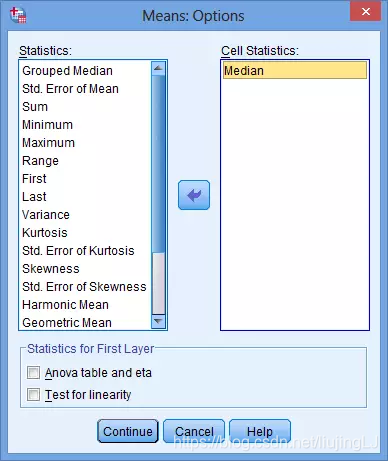
5. 点击Continue,返回Means对话框。
6. 点击OK,得到结果。
结果解读
1. Mann-Whitney U检验结果
本例中男性组和女性组的数据分布相似,因为我们先解读数据分布相似时的结果,使用旧对话框得出的结果如下图所示:
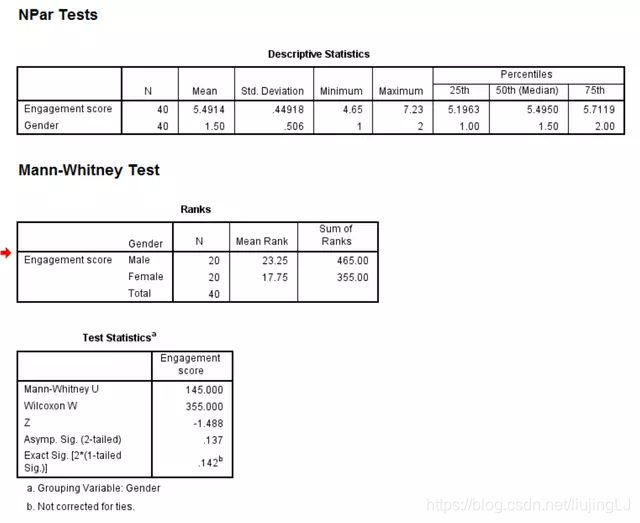
Test Statistics表格中Mann-Whitney U代表检验的U统计量值为145;Z代表Z值;Asymp.Sig(2-tailed)代表渐进P值;Exact Sig[2*(1-tailed Sig.)]代表精确P值。
样本量越大,渐进P值就越接近真实P值。当每个分组的样本量小于20时,SPSS软件会自动计算精确P值,此时选择精确P值来判断检验假设。当样本量大于20时,渐进P值可以很好地代表真正的P值,因此选择渐进P值来判断检验假设。
本例中每组的样本量为20个,结果报告了精确P值为0.142,本例选用精确P值判断检验假设,P值大于界值0.05,因此不能拒绝原假设,即不能认为男性组和女性组的广告接受程度有统计学差异。
提示:如果在SPSS报告的结果中发现渐进P值与精确P值显示为“0.000”,这意味着P值小于0.0005,并不是真的为0。
2. 计算中位数输入结果
在本文的第六步中可以计算出各组的中位数值如下图:

【Median:中位数;gender:性别;engagement:接受度评分;Male:男性;Female:女性;Total:全部;】
3. 计算结果的表达
① 数据分布相同的结果表达——中位数
中文表述:使用Mann-Whitney U检验判断男性与女性对于此药品广告的接受程度是否有差异。通过柱形图可以判断两组接受程度评分的数据分布相似。男性组中接受度评分的中位数为5.58,女性组中接受度评分的中位数为5.38。Mann-Whitney U检验结果显示男性组与女性组的接受度评分差异没有统计学意义,U=145,Z=-1.488,P=0.142。
英文表述:A Mann-Whitney U test was run to determine if there were differences in engagement score between males and females. Distributions of the engagement scores for males and females were similar, as assessed by visual inspection. Median engagement score for males (5.58) and females (5.38) was not statistically significantly different, U = 145, z = -1.488, p = .142, using an exact sampling distribution for U (Dineen & Blakesley, 1973).
② 数据分布不同的结果表达——平均秩次
如果在实际的数据计算中发现各分组中数据的分布形状不同,则不能用中位数进行比较,需要对各组的数据进行编秩,算出平均秩次。
中文表述:使用Mann-Whitney U检验判断男性与女性对于此药品广告的接受程度是否有差异。通过柱形图可以判断两组接受程度评分的数据分布不同。Mann-Whitney U检验结果显示男性组(平均秩次为23.25)与女性组(平均秩次为17.75)对于此药品广告的接受度评分差异没有统计学意义,U=145,Z=-1.488,P=0.142。
英文表述:A Mann-Whitney U test was run to determine if there were differences in engagement score between males and females. Distributions of the engagement scores for males and females were not similar, as assessed by visual inspection. Engagement scores for males (mean rank = 23.25) and females (mean rank = 17.75) were not statistically significantly different, U = 145, z = -1.488, p = .142, using an exact sampling distribution for U (Dineen & Blakesley, 1973).