Move mean滑动平均差法

直接上代码，原理可以看这个文章。

DOI: 10.11821/dlxb201811003

#滑动平均差法
Q <- read.csv("D:/OneDrive/UCAS/stu/2022zdx/zdx_data.csv")
n <- length(Q$Runoff)
p <- 19 #假定时间序列周期Moavse <- function(Q,n,p){MU <- vector(length=n-1)MD <- vector(length=n-1)detaM <- vector(length=n-1)k <- 0for(i in 2:n){if(p>=i-1){k <- i-1}else(k <- p)MU[i] <- 1/k*(sum(Q[c((i-k):(i-1))]))#正向滑动序列if(p>=n-i+1){k <- n-i+1}else(k <- p)MD[i] <- 1/k*(sum(Q[c(i:(i+k-1))]))#逆向滑动序列}detaM <- abs(MU-MD)results <- cbind(MU,MD,detaM)return(results)
}
detaQr <- Moavse(Q$Runoff,n,p)
max3 <- order(detaQr[,3],decreasing=TRUE)[1:3] + 1978plot(x=Q$year,y=detaQr[,3],lty=2,lwd=2,xlab = "time",ylab="deltaM",type="l", col = "blue", ylim = c(-6, 32), main = "Move mean test")
par(new = TRUE)plot(Q$year, Q$Runoff,col="red",lwd=1.5,type="l", xaxt = "n", yaxt = "n", ylim = c(40, 200),ylab = "", xlab = "")
axis(side = 4)
mtext("Runoff", side = 4, line = 1)
legend("topright", c("derltaM", "Runoff"),col = c("blue", "red"), lty = c(1, 2))

由于需要绘制两个轴，设置xaxt和yaxt是为了不显示坐标轴内容，再用mtext手动添加。side是文字的位置（上下左右，4是右面）

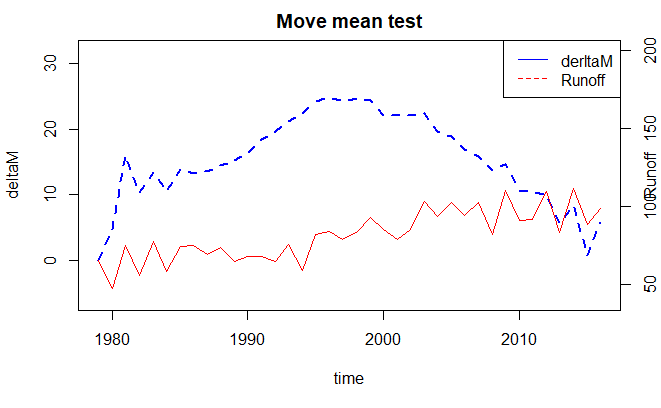
如图所示，derltaM取极值的时候认为发生了突变。我把原理稍微画了个图方便理解，如下。该算法主要考虑了周期性，假定周期性前向和后向差距不大，derltaM是前向减去后向，最大值就是突变点了。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Siuhk4CI-1667644231215)(https://imagecollection.oss-cn-beijing.aliyuncs.com/img/QQ%E5%9B%BE%E7%89%8720221105175144.jpg)]

Mann Kendall突变检验

参考：http://www.r-china.net/forum.php?mod=viewthread&tid=723

Mann_Kendall <- function(timeserial){#Mann Kendall 突变检验，传递参数Mann_Kendall_sub <- function(timeserial){#需要进行两次秩的分析，因此在函数中嵌套了一个函数r <- c()#分析的三个变量，具体含义可以参照魏凤英老师的书s <- c()#秩序列。U <- c()for(i in 2:length(timeserial))#进行大小比较，从第二个开始与以前的数据进行大小比较{r[i] <- 0for(j in 1:i){if(timeserial[i]>timeserial[j]){r[i] <- r[i]+1}#如果后面的数大于前面的数，则秩加1}s[i] <- 0for (ii in 2:i){s[i] <- s[i] + r[ii]#秩序列。Sk是第i时刻数值大于ii时刻数值个数的累计数}U[i] <- 0U[i] <- (s[i] - (i * (i - 1) / 4))/sqrt(i * (i - 1) * (2 * i + 5) / 72)}r[1] <- 0s[1] <- 0U[1] <- 0LST <- list(r = r, s = s, U = U)return (LST)}timeserial_rev <- rev(timeserial)#生成逆序列y1 <- Mann_Kendall_sub(timeserial)#计算正序列y2 <- Mann_Kendall_sub(timeserial_rev)#计算逆序列y2$U <- -(rev(y2$U))#转换符号与顺序LST <- list(UF=y1,UB=y2)return(LST)  
}Q <- read.csv("D:/OneDrive/UCAS/stu/2022zdx/zdx_data.csv")d <- Mann_Kendall(Q$Runoff)#进行突变检验
yUF <- as.data.frame(d$UF[3])$U
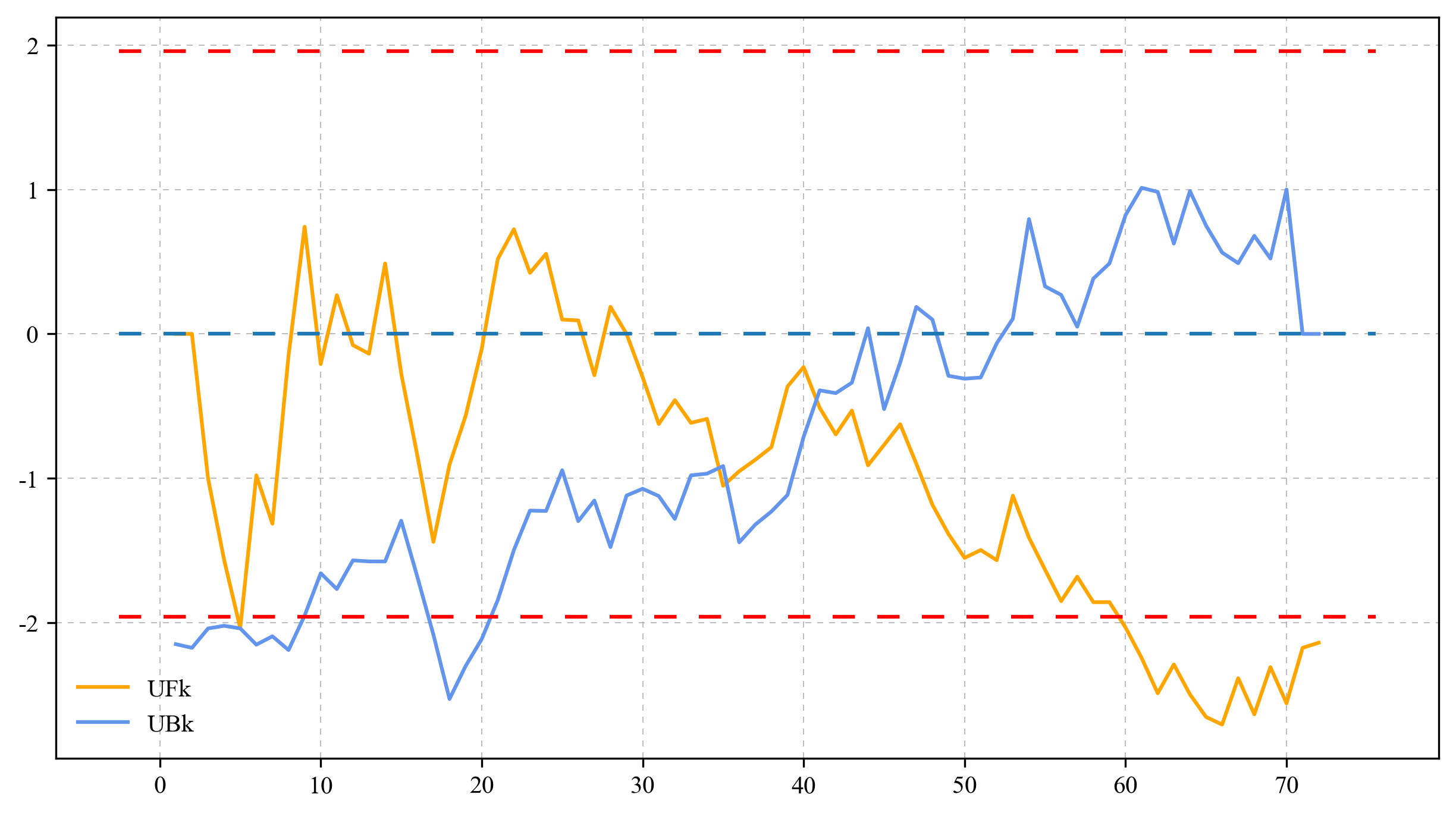
yUB <- as.data.frame(d$UB[3])$Uplot(x=c(1:length(Q$year)),y=yUF, type="l", ylim=c(min(yUF,yUB,-1.96),max(yUF,yUB,1.96)),lwd=1, lty=5, ylab="", cex=0.5,xaxt="n",mgp=c(1,0.1,0),tck=-0.02)
points(x=c(1:length(Q$year)),y=yUB,type="l",lty=3,col=6,lwd=1)
abline(h=1.969,lty=4,lwd=0.5)# 1.969是a=0.05的显著性水平
abline(h=-1.96,lty=4,lwd=0.5)
abline(h=0,col="gray",lwd=0.5)

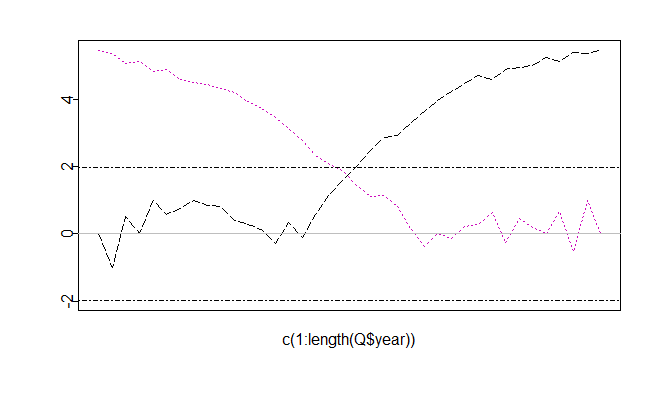
该方法的原理是：

在构建秩序列后，进而计算累积序列值。当没有突变点时，秩的增长将是自然的并且符合某种分布（如正态分布），这时就可以进行假设性检验。（个人理解，若有不对欢迎指出~）

R包cmp做突变点检验

有现成的R包可以做突变检验，可以使用下列参数：

参考：https://zhuanlan.zhihu.com/p/350235881

Arguments	Condition
Student	Gaussian sequence
Bartlett	Gaussian sequence
GLR	Gaussian sequence
Exponential	Exponentially distributed sequence
GLRAdjusted; ExponentialAdjusted	Identical to the GLR and Exponential statistics
FET	Bernoulli sequence
Mann-Whitney	non-Gaussian distribution
Mood	non-Gaussian distribution
Lepage	non-Gaussian distribution
Kolmogorov-Smirnov	non-Gaussian distribution
Cramer-von-Mises	non-Gaussian distribution

# library
library(cpm)
cpm.res = processStream(Q$Runoff, cpmType = "Kolmogorov-Smirnov")
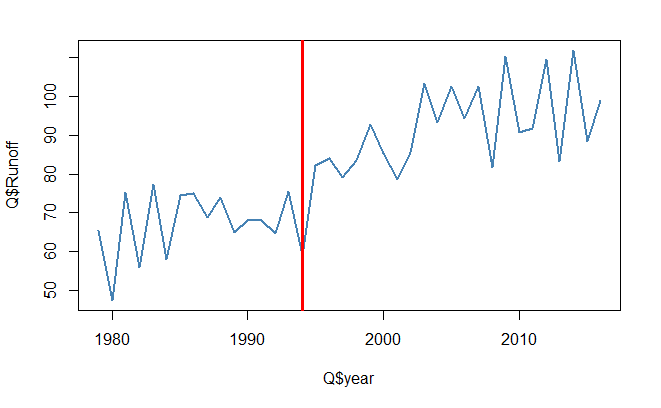
# 可视化变点
plot(Q$year, Q$Runoff, type = "l", col = "steelblue", lwd = 2)
abline(v = cpm.res$changePoints + 1978, lwd = 3.5, col = "red")
# 变点坐标信息提取
print(cpm.res$changePoints)