在点云处理领域，KD-Tree是一种常用的数据结构，用于加速近似最近邻搜索(Nearest Neighbor Search)、点云分割(Segmentation)、物体识别(Object Recognition)、三维重建(3D Reconstruction)等操作。本篇博客将详细介绍KD-Tree的原理、构建和应用。

一、KD-Tree原理

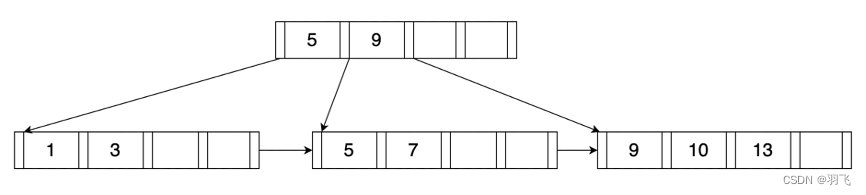
KD-Tree(K-Dimensional Tree)，是一种二叉搜索树(binary search tree)，通常用于解决k维空间中最近邻搜索问题。它的构建过程是通过不断地分割空间，构建一颗二叉树，将每个数据点分配到树的节点中，以实现高效的搜索。

其实现方法为：首先选择一个维度，将所有数据按照这个维度的大小排序，然后选择中位数作为分割点，将数据集分为两个子集，小于等于分割点的放在左子树中，大于分割点的放在右子树中。递归地对子集进行同样的操作，直到数据集中的数据被分到叶子节点为止。

KD-Tree的搜索操作是在树上递归搜索的过程。从根节点开始，根据搜索点的位置，沿着树往下搜索。在每个节点上，先判断该节点对应的点是否比当前最优解更优，如果更优则更新最优解。然后根据搜索点与分割平面的位置关系，选择进入左子树或右子树进行递归搜索。

二、KD-Tree构建

KD-Tree的构建过程通常有两种方法，分别是递归和迭代。递归的方法简单易懂，但是会导致栈溢出的问题；迭代方法需要用到队列或堆栈，相对而言比较麻烦，但是不会产生栈溢出的问题。这里介绍递归构建的方法。

首先确定树的根节点，将所有数据点存储在该节点的数据集中。然后选择一个维度，计算该维度的中位数，并将该中位数作为节点的分割点。接下来将数据集中小于等于分割点的数据分配给左子树，大于分割点的数据分配给右子树。递归地对子树进行同样的操作，直到数据集中的数据被分到叶子节点为止。

三、KD-Tree应用

近似最近邻搜索
在KD-Tree上进行最近邻搜索的复杂度为O(log n)，相对于暴力搜索的O(n)要快很多。最近邻搜索通常用于图像匹配、物体识别、运动控制等领域。例如，在物体识别中，可以将每个物体的特征向量表示为一个点云，然后利用KD-Tree搜索待识别物体的最近邻点云，从而实现物体识别。

点云分割
点云分割是指将一个点云分成若干个部分的过程，每个部分包含一组具有相似特征的点。例如，可以将点云中的每个点的法向量作为特征，然后利用KD-Tree将点云分割成若干个局部区域，从而实现点云分割。

三维重建
在三维重建中，KD-Tree可以用于实现点云的采样和重构。例如，在点云采样中，可以利用KD-Tree选择最具代表性的点，从而减少点云数据的数量；在点云重构中，可以将点云拟合成三角网格，从而实现三维重建。

总结：

KD-Tree是一种用于加速点云处理的数据结构，其原理是通过递归地分割空间，构建一颗二叉树，以实现高效的最近邻搜索、点云分割、三维重建等操作。虽然KD-Tree的构建和应用相对较为复杂，但是在实际应用中可以显著提高点云处理的效率和精度。