x.1 Classification 分类问题理论
x.1.1 Classification和Regression的区别
注意,广义上来讲,Classification/Softmax Regression 和 Linear Regression 都属于线性模型。但人们口语上更习惯用Classification表示Softmax Regression,而用Regression表示Linear Regression。
例如预测房屋出售价格就是一个典型的Linear Regression线性回归问题,而有时我们比起how much更关心category,例如给一些特征判断患者是否患有癌症,由此产生的便是Classification分类问题。
x.1.2 One-hot Encoding
Classification问题的输出往往并不与类别之间的自然顺序有关,因此有时候并不能将问题转化为Regression问题,为此统计学家发明了一种用于表示分类数据的简单方法:one-hot encoding独热编码。one-hot encoding是一个向量,它的长度对应类别总数,类别对应的分量的位置设置为1,其余位置设置为0,例如 y ∈ { ( 1 , 0 , 0 ) , ( 0 , 1 , 0 ) , ( 0 , 0 , 1 ) } y \in \{(1, 0, 0), (0, 1, 0), (0, 0, 1)\} y∈{(1,0,0),(0,1,0),(0,0,1)}
x.1.3 Model Architecture
Classification和Regression 模型的区别在于Classification是多输出,因此我们也需要和输出具有同样数量的bias偏置。例如我们具有4个输入,3个输出,则需要12个weight scalars权重标量,和3个bias scalars偏置标量,共计15个可学习参数,如下:
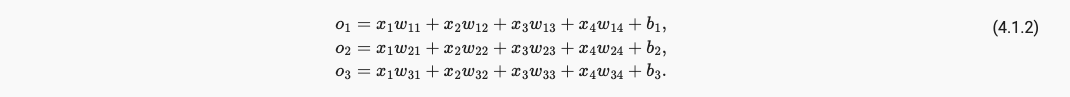

为了简化模型,我们通过矩阵形式来表达运算,其中W是一个3x4的矩阵,而b是一个长度为3的向量。
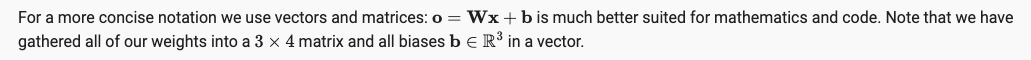
可见,由层数为2,全连接层产生的网络模型,它的参数量一直都是 O ( d p ) , d = 输入 , p = 输出 O(dp), d=输入, p=输出 O(dp),d=输入,p=输出。
x.1.4 Softmax
存在问题:
- 输出数值总和不一定为1
- 输出可能为负数甚至大于1
上面这些都不符合概率论基本公理,为了解决问题引入Softmax,
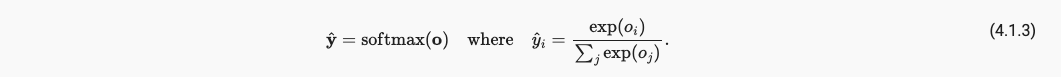
softmax具备的好处,
- 将预测变换为非负数且总和为1。
- 让模型保持可导的性质,即导数易求。
- softmax不会改变未规范化的预测间的次序,所以下式仍然成立,
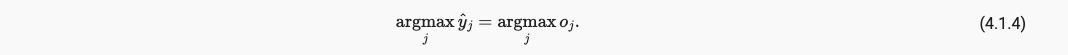
最终,我们的引入softmax的网络模型如下:
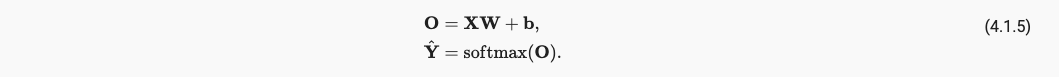
x.1.5 Mini-batch Gradient Descent
batch size = 1, stochastic gradient descent (SGD)
batch size = n, 1 < n < 256, stochastic gradient descent (MBSGD)
batch size = 256, mini-batch gradient descent (MBGD/BGD) , 因为使用了全部数据集
在这里使用了mini-batch SGD小批量随机梯度下降(后称MBSGD)算法,因为相较于一次处理一个样本,MBSGD加快了XW的矩阵-向量乘法。
例如我们读取了一个批量的样本X,其中输入的特征维度为d,批量大小为n,输出类别数为q。则立即推小样本的特征为 X ∈ R n × d , 权重为 W ∈ R d × q , 偏置为 b ∈ R 1 × q X \in R^{n\times d}, 权重为W \in R^{d \times q}, 偏置为 b \in R^{1 \times q} X∈Rn×d,权重为W∈Rd×q,偏置为b∈R1×q,如下,
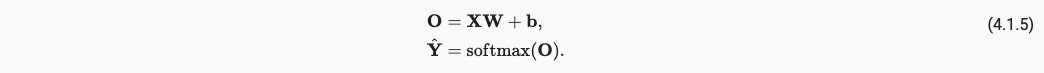
batch_size也不一定越大越好,考虑到BN层的存在,一般需要大于8,batch_size大小要和learning rate匹配。所以可学习参数的数量和batch_size无关。
关于梯度下降算法这里有一篇很不错的文章:深度学习——优化器算法Optimizer详解(BGD、SGD、MBGD、Momentum、NAG、Adagrad、Adadelta、RMSprop、Adam)https://www.cnblogs.com/guoyaohua/p/8542554.html
建议使用Adam优化器,且超参数设置为 β1 = 0.9,β2 = 0.999,ϵ = 10e−8
x.1.5 Cross-entropy Loss
由于MLE极大似然估计我们得到损失函数为cross-entropy loss交叉熵损失。假设我们有q个类别,最终我们得到的target - y和predict - y_hat的损失函数为,

请注意,式中的yi是一个one-hot encoding形式。我们将式(4, 1, 8)中引入softmax激活函数,使的output_j也变成一个概率分布的形式,
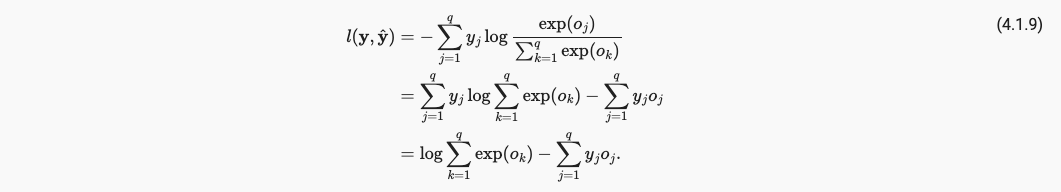
对上面loss针对某一特定输出 o j o_j oj求偏导,得到loss对于某一特定输出的o_j的偏导就是softmax该o_j再减去y_j的one-hot encoding,所以引入softmax激活层的网络模型的导数是方便求解的。
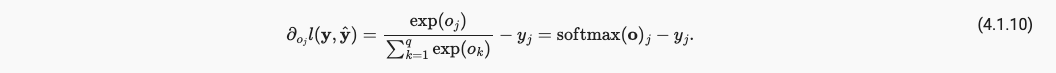
x.2 Classification 分类问题实践
将图片数据展平成一维的再传入全连接层训练。
F.cross_entropy()和nn.CrossEntropyLoss()没有太大区别,但是要注意nn.Dropout和F.dropout()具有很大区别,虽然dropout无可学习参数,但是model.train()和model.eval()无法控制F.dropout只可以控制nn.Dropout。