题意
爱与愁大神后院里种了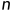 
棵樱花树，每棵都有美学值 
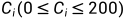。爱与愁大神在每天上学前都会来赏花。爱与愁大神可是生物学霸，他懂得如何欣赏樱花：一种樱花树看一遍过，一种樱花树最多看 
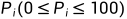遍，一种樱花树可以看无数遍。但是看每棵樱花树都有一定的时间 
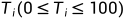。爱与愁大神离去上学的时间只剩下一小会儿了。求解看哪几棵樱花树能使美学值最高且爱与愁大神能准时（或提早）去上学。
思路
首先很明确：这是一道背包问题，空间和价值都非常明确（空间即时间，价值即美学值），“看一遍“”看无数遍”“看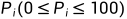遍”对应了三种背包：01背包、完全背包和多重背包，所以我们直接分类处理就好啦！
读入时间可以直接用scanf来处理，十分方便。但是写完提交发现两个TLE后我们发现了问题：朴素的多重背包是经不住毒瘤数据的洗礼的。
我们需要优化！！
这里可以对多重背包使用二进制优化：将n个物品拆成1+2+4+...+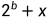
的形式（其中x是余项），此时选择1~n个物品等价于选择1个物品、2个物品、4个物品、......、
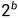个物品和x个物品里的其中若干个，所以直接把n个物品进行拆分是可行的。
这样我们就可以把多重背包转换为01背包了！而完全背包也可以看作数量巨大的多重背包，最后转化为01背包进行处理。
自此，这道题在一通拆分后只剩下对01背包的处理了，这里不多赘述，直接上代码吧。
代码
#include <iostream>
using namespace std;
int shh, smm, ehh, emm, T;
int n;
int p[500000], c[500000], t[500000];
int dp[1005];int main() {scanf("%d:%d %d:%d", &shh, &smm, &ehh, &emm);T = (ehh - shh) * 60 + (emm - smm);cin >> n;int temN = n;for (int i = 1; i <= temN; ++i) {cin >> t[i] >> c[i] >> p[i];if (p[i] == 0)p[i] = 999999;if (p[i] != 1) {int x = 1;int sumX = 0;while (sumX + x < p[i]) { //二进制拆分的方法（以8为例）： 8 = 1 + 2 + 4 + 1t[++n] = t[i] * x;p[n] = 1;c[n] = c[i] * x;sumX += x;x <<= 1;}x = p[i] - sumX;t[i] = t[i] * x;p[i] = 1;c[i] = c[i] * x;}}for (int i = 1; i <= n; ++i) {if (c[i] == 0)continue;for (int j = T; j >= t[i]; --j) {dp[j] = max(dp[j], dp[j - t[i]] + c[i]);//cout << j << " " << dp[j] << endl;}}cout << dp[T];return 0;
}
