[入门必看]数据结构2.3：线性表的链式表示

第二章线性表
2.3 线性表的链式表示
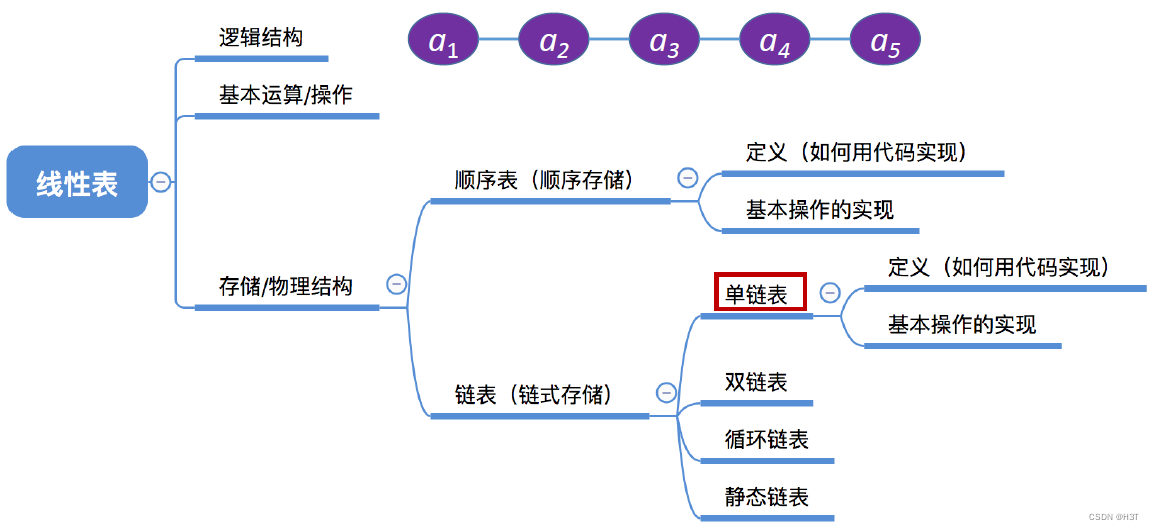
- 知识总览
- - 2.3.1 单链表的定义
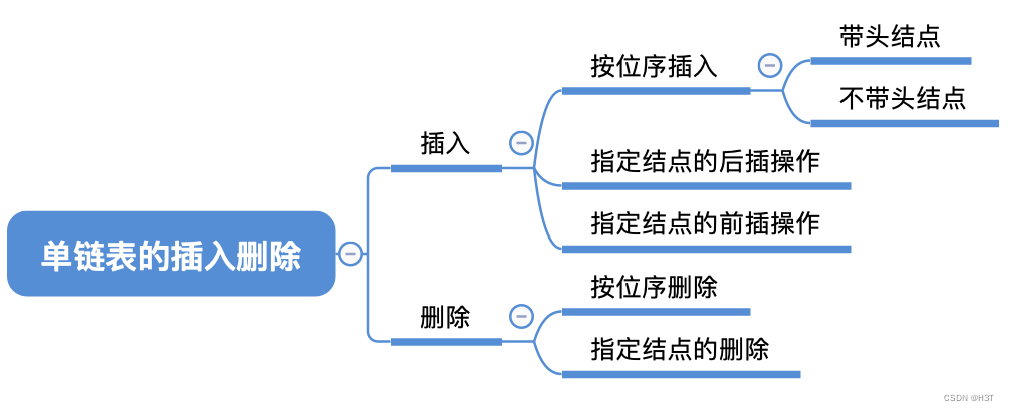
  - 2.3.2_1 单链表的插入删除
  - 2.3.2_2 单链表的查找
  - 2.3.2_3 单链表的建立
  - 2.3.3 双链表
  - 2.3.4 循环链表
  - 2.3.5 静态链表
  - 2.3.6 顺序表和链表的比较
- 2.3.1 单链表的定义
- - 单链表的实现
  - - 使用typedef关键字 —— 数据类型重命名
    - 初始化单链表
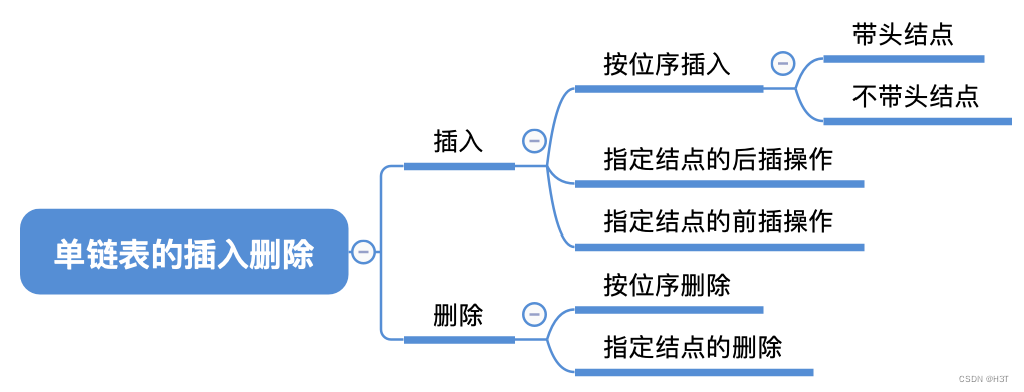
- 2.3.2_1 单链表的插入和删除
- - 按位序的插入（带头结点）
  - 按位序的插入（不带头结点）
  - 指定结点的后插操作
  - 指定结点的前插操作
  - 按位序删除（带头结点）
  - 指定结点的删除
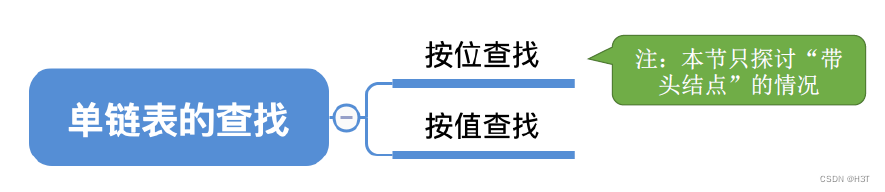
- 2.3.2_2 单链表的查找
- - 按位查找
  - - 封装（基本操作）的好处
  - 按值查找
  - 求表的长度
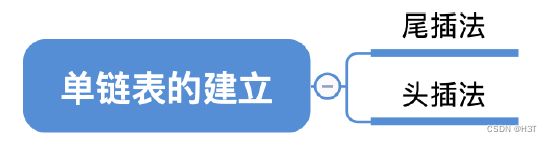
- 2.3.2_3 单链表的建立
- - 尾插法建立单链表
  - 头插法建立单链表
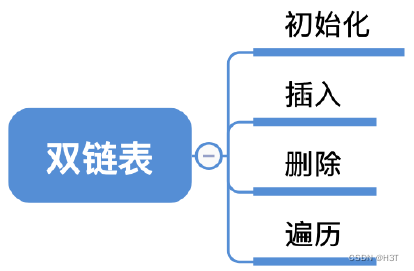
- 2.3.3 双链表
- - 单链表V.S.双链表
  - 初始化双链表（带头结点）
  - 双链表的插入
  - 双链表的删除
  - 双链表的遍历
- 2.3.4 循环链表
- - 循环单链表
  - 循环双链表
- 2.3.5 静态链表
- - 什么是静态链表
  - 静态链表的定义
  - 静态链表的基本操作
- 2.3.6 顺序表和链表的比较
- - 逻辑结构
  - 存储结构
  - 基本操作
  - - a. 创
    - b. 销
    - c. 增删
    - d. 查
  - 如何选择
  - 开放式问题的答题思路
知识回顾与重要考点
- 2.3.1 单链表的定义
- 2.3.2_1 单链表的插入和删除
- 2.3.2_2 单链表的查找
- 2.3.2_3 单链表的建立
- 2.3.3 双链表
- 2.3.4 循环链表
- 2.3.5 静态链表
- 2.3.6 顺序表和链表的比较

第二章线性表

小题考频：5
大题考频：12

2.3 线性表的链式表示

难度：☆☆☆☆

知识总览

在这里插入图片描述

2.3.1 单链表的定义

在这里插入图片描述

2.3.2_1 单链表的插入删除

在这里插入图片描述

2.3.2_2 单链表的查找

在这里插入图片描述

GetElem(L,i)：按位查找操作。获取表L中第i个位置的元素的值。
LocateElem(L,e)：按值查找操作。在表L中查找具有给定关键字值的元素。

2.3.2_3 单链表的建立

在这里插入图片描述

Step 1：初始化一个单链表
Step 2：每次取一个数据元素，插入到表尾/表头
——本节探讨带头结点的情况

2.3.3 双链表

在这里插入图片描述

2.3.4 循环链表

在这里插入图片描述

2.3.5 静态链表

在这里插入图片描述

2.3.6 顺序表和链表的比较

在这里插入图片描述

2.3.1 单链表的定义

在这里插入图片描述

顺序表 - 连续存放，每个结点中只存放数据元素

优点：可随机存储，存储密度高
缺点：要求大片连续空间，改变容量不方便

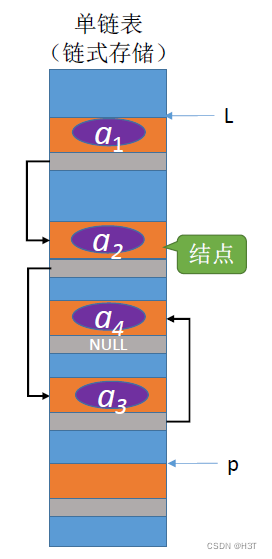
单链表——通过“链”建立元素间的逻辑关系
——每个结点除了存放数据元素外，还要存储指向下一个结点的指针。

优点：不要求大片连续空间，改变容量方便
缺点：不可随机存取，要耗费一定空间存放指针

在这里插入图片描述

单链表的实现

struct LNode{ //定义单链表结点类型 - 结点ElemType data; //每个结点存放一个数据元素 - 数据域struct LNode *next; //指针指向下一个结点 - 指针域
};

增加一个新的结点：在内存中通过malloc申请一个结点所需空间，并用指针p指向这个结点，并设计把p插入到单链表中

struct LNode *p = (struct LNode *) malloc(sizeof(struct LNode));

每次都要写struct LNode *p —— 太麻烦！

使用typedef关键字 —— 数据类型重命名

typedef <数据类型> <别名>

Eg1_int型.

typedef int zhengshu;
typedef int *zhengshuzhizhen;
int x = 1;
zhengshu x =1; //和上一句等价
int *p;
zhengshuzhizhen p; //和上一句等价

Eg2_结构体struct.

typedef struct LNode LNode;
LNode *p = (LNode*) malloc(sizeof(LNode));

定义结构体还有更简洁的写法！
——可以直接将指针重命名*LinkList

typedef struct LNode{ ElemType data; struct LNode *next; 
}LNode, *LinkList;//其等价于
struct LNode{ ElemType data; struct LNode *next; 
};
typedef struct LNode LNode;
typedef struct LNode *LinkList;

要表示一个单链表时，只需声明一个头指针L，指向单链表的第一个结点：

LNode *L; //声明一个指向单链表第一个结点的指针
//等价于
LinkList L; //适当选择写法，代码可读性更强

LNode是一个普通的结构体名，相当于将结构体类型struct LNode重命名为LNode - 指结点;
*LinkList是一个指针类型，相当于将struct LNode* 重命名为LinkList - 指单链表。

Eg.
在这里插入图片描述
强调这是一个单链表——使用LinkList
强调这是一个结点 ——使用LNode *

初始化单链表

不带头结点的单链表

初始化单链表

//定义单链表结点类型
typedef struct LNode{ ElemType data; struct LNode *next; 
}LNode, *LinkList;//初始化一个空的单链表
bool InitList(LinkList &L){ //需要修改L，传入引用“&L”L = NULL; //空表，暂时还没有任何结点 - 防止脏数据return true;
}void test(){LinkList L; //声明一个指向单链表的指针//初始化一个空表InitList(L);//…
}

在这里插入图片描述
判断单链表是否为空

//判断单链表是否为空
bool Empty(LinkList L){if(L == NULL)return true;elsereturn false;
}

判断单链表是否为空的更简洁的写法：

bool Empty(LinkList L){return(L == NULL);	//该条的运算结果就是true或false，直接return即可
}

带头结点的单链表

初始化单链表

//定义单链表结点类型
typedef struct LNode{ ElemType data; struct LNode *next; 
}LNode, *LinkList;//初始化一个单链表（带头结点）
bool InitList(LinkList &L){ //需要修改L，传入引用“&L”L = (LNode *) malloc(sizeof(LNode)); //分配一个头结点 - 头结点不存储数据if(L == NULL) //内存不足，分配失败return false;L->next = NULL; //头结点之后暂时还没有结点return true;
}void test(){LinkList L; //声明一个指向单链表的指针//初始化一个空表InitList(L);//…
}

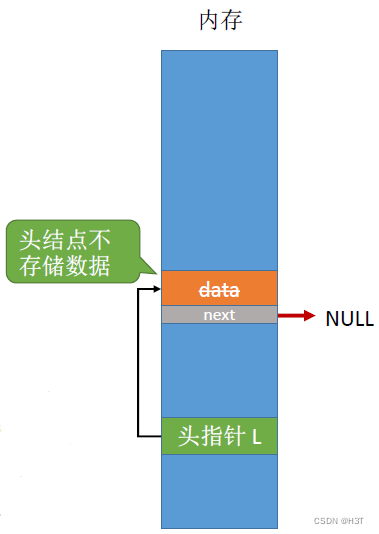
在这里插入图片描述

头结点不存储数据

判断单链表是否为空

//判断单链表是否为空（带头结点）
bool Empty(LinkList L){if(L->next == NULL)return true;elsereturn false;
}

不带头结点 V.S.带头结点——区别

不带头结点，写代码更麻烦
对第一个数据结点和后续数据结点的处理需要用不同的代码逻辑
对空表和非空表的处理需要用不同的代码逻辑

大多数情况下选择使用带头结点的方式实现，更方便。

2.3.2_1 单链表的插入和删除

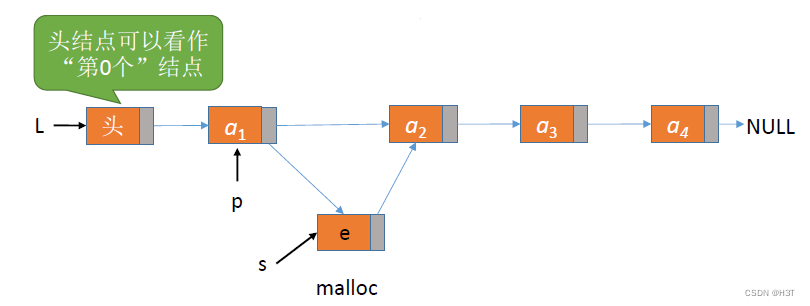
在这里插入图片描述

按位序的插入（带头结点）

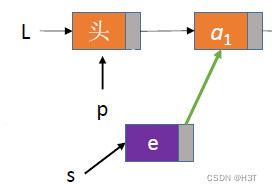
ListInsert(&L,i,e)：插入操作。在表L中的第i个位置上插入指定元素e。

找到第i-1个结点，将新结点插入其后

在这里插入图片描述
代码实现：

typedef struct LNode{ ElemType data; struct LNode *next; 
}LNode, *LinkList;//在第i个位置插入元素e（带头结点）
bool ListInsert(LinkList &L, int i, ElemType e){if (i<1) //不合法return false;LNode *p; //需要指针p指向当前扫描到的i-1结点p = L; //p指向头结点L，头结点是第0个结点（不存数据）int j = 0; //记录当前p指向的是第几个结点 - 此时j为0个结点（头结点）while (p != NULL && j<i-1){ //循环，直到找到第i-1个结点 - 指针p指向p = p->next;j++;}if (p == NULL) //i值不合法return false;LNode *s = (LNode *) malloc(sizeof(LNode)); //为新结点申请一片空间s->data = e; //新结点数据域s->next = p->next; //s结点指向p之后的一个结点p->next = s; //p结点指向s结点 - 将结点s连到p之后//以上两步顺序不可以颠倒！return true; //插入成功
}

分析：

如果i=1（插在表头）

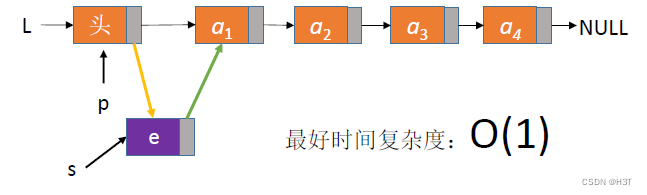
此时为最好时间复杂度： $O (1)$

这两句的顺序不可颠倒。
s->next = p->next; 
p->next = s; //将结点s连到p之后
Step1：

Step2：

若颠倒这两句的顺序！
p->next = s;
s->next = p->next;
Step1：

Step2：

不对！

如果i=3（插在表中）

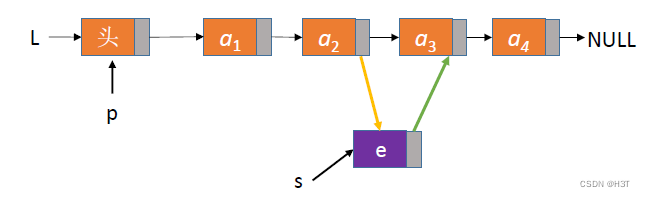
在这里插入图片描述
3. 如果i=5（插在表尾）

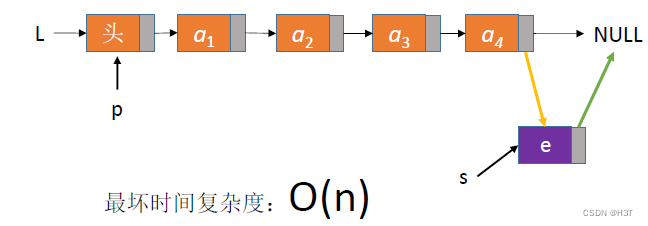
此时为最坏时间复杂度： $O (n)$

如果i=6（i>Length）
此时p不合法，无法插入

按位序插入操作的时间复杂度：
$O (n)$

按位序的插入（不带头结点）

ListInsert(&L,i,e)：插入操作。在表L中的第i个位置上插入指定元素e。
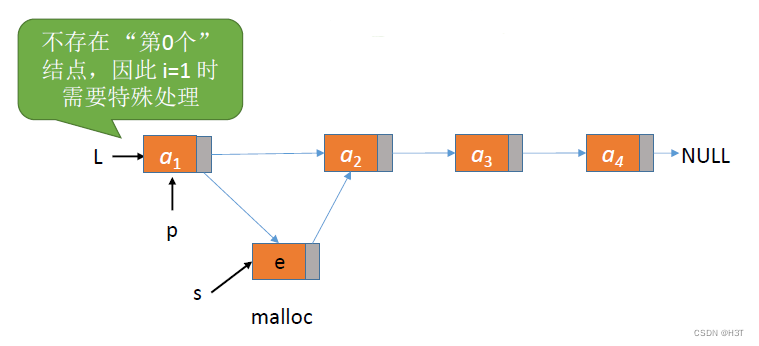
在这里插入图片描述
代码实现：

typedef struct LNode{ElemType data;struct LNode *next
}LNode, *LinkList;bool ListInsert(LinkList &L, int i, ElemType e){if (i < 1)return false;if (i == 1){ //插入第1个结点的操作与其他结点操作不同LNode *s = (LNode *) malloc(sizeof(LNode));s->data = e;s->next = L;L = s; //头指针指向新结点return true;}LNode *p; //指针p指向当前扫描到的结点int j = 1; //当前p指向的是第几个结点p = L; //p指向第1个结点（注意：不是头结点）while (p != NULL && j < i - 1){ //循环找到第i-1个结点p = p->next;j++;}if (p == NULL) //i值不合法return false;LNode *s = (LNode *) malloc(sizeof(LNode));s->data = e;s->next = p->next;p->next = s;return true; //插入成功
}

分析：

如果i=1（插在表头）

如果不带头结点，则插入、删除第1个元素时，需要更改头指针L
如果i>1…
此时后续逻辑和带头结点的一样

结论：不带头结点写代码更不方便，推荐用带头结点的

注意：考试中带头、不带头都有可能考察，注意审题

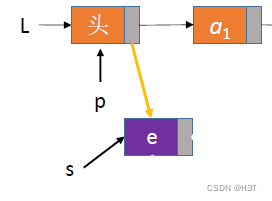
指定结点的后插操作

——给定一个结点，在该结点后插入一个数据元素e

代码实现：

typedef struct LNode{ElemType data;struct LNode *next;
}LNode, *LinkList;//后插操作：在p结点之后插入元素e
bool InsertNextNode(LNode *p, ElemType e){if (p == NULL)return false;LNode *s = (LNode *) malloc(sizeof(LNode));if (s == NULL) //内存分配失败（如内存不足）return false;s->data = e; //用结点s保存数据元素es->next = p->next;p->next = s; //将结点s连到p之后return true;
}

在这里插入图片描述
时间复杂度： $O (1)$

有了后插操作的子函数后，在第i个位置插入元素e就可以调用后查操作的函数来完成：

typedef struct LNode{ElemType data;struct LNode *next;
}LNode, *LinkList;//后插操作：在p结点之后插入元素e
bool InsertNextNode(LNode *p, ElemType e){if (p == NULL)return false;LNode *s = (LNode *) malloc(sizeof(LNode));if (s == NULL) //内存分配失败（如内存不足）return false;s->data = e; //用结点s保存数据元素es->next = p->next;p->next = s; //将结点s连到p之后return true;//在第i个位置插入元素e（带头结点）
bool ListInsert(LinkList &L, int i, ElemType e){if (i<1) //不合法return false;LNode *p; //需要指针p指向当前扫描到的i-1结点p = L; //p指向头结点L，头结点是第0个结点（不存数据）int j = 0; //记录当前p指向的是第几个结点 - 此时j为0个结点（头结点）while (p != NULL && j<i-1){ //循环，直到找到第i-1个结点 - 指针p指向p = p->next;j++;}return InsertNextNode(p, e);
}

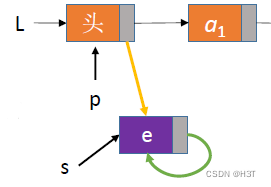
指定结点的前插操作

如果：

//前插操作：在p结点之前插入元素e
bool InsertPriorNode (LNode *p, ElemType e)

出现了问题，p结点前的区域是未知的
——如何找到p结点的前驱结点？
在这里插入图片描述
传入头指针！

//前插操作：在p结点之前插入元素e
bool InsertPriorNode (LinkList L, LNode *p, ElemType e)

在这里插入图片描述
通过循环查找p的前驱结点q，再对q后插。
时间复杂度： $O (n)$

换一个思路 —— 偷天换日：

先在p后插一个新结点s，再讲p结点的数据复制到s中，最后将要插入的元素e传入p结点。

代码实现：

typedef struct LNode{ElemType data;struct LNode *next;
}LNode, *LinkList;//后插操作：在p结点之后插入元素e
bool InsertPriorNode(LNode *p, ElemType e){if (p == NULL)return false;LNode *s = (LNode *) malloc(sizeof(LNode));if (s == NULL) //内存分配失败（如内存不足）return false;s->next = p->next;p->next = s; //将结点s连到p之后s->data = p->data; //将p中元素复制到s中p->data = e; //p中元素覆盖为ereturn true;
}

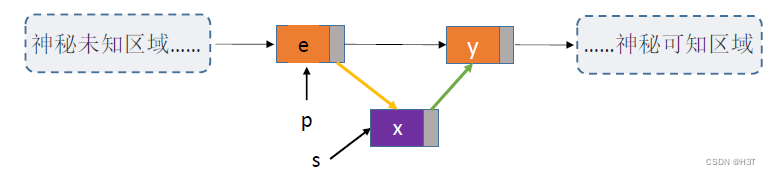
在这里插入图片描述
时间复杂度： $O (1)$

另一版本：
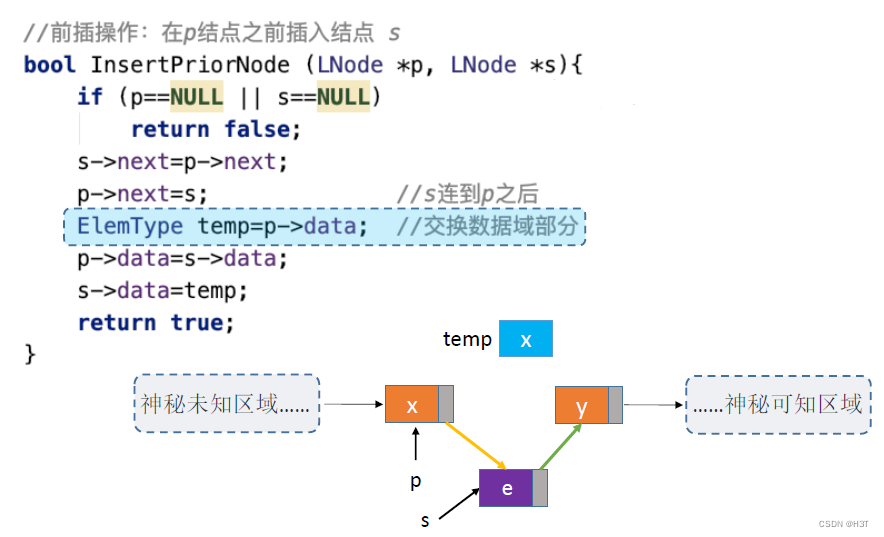
在这里插入图片描述

借助辅助变量temp保存p结点内容，再将s结点内容复制到p结点，最后将辅助变量temp复制到s，完成交换。

按位序删除（带头结点）

ListDelete(&L,i,&e)：删除操作。删除表L中第i个位置的元素，并用e返回删除元素的值。

找到第i-1个结点，将其指针指向第i+1个结点，并释放第i个结点

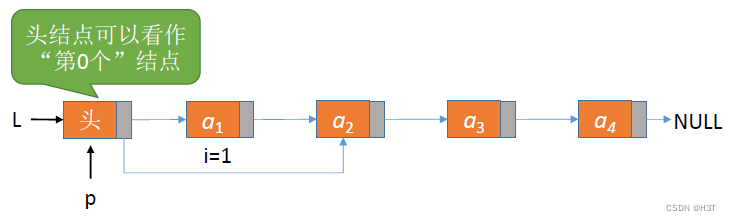
在这里插入图片描述
代码实现

typedef struct LNode{ElemType data;struct LNode *next;
}LNode, *LinkList;bool ListDelete(LinkList &L, int i, ElemType &e){if (i < 1)return false;LNode *p; //指针p指向当前扫描到的结点int j = 0; //当前p指向的是第几个结点p = L; //L指向头结点，头结点是第0个结点（不存数据）while (p != NULL && j < i - 1){ //循环找到第i-1个结点p = p->next;j++;}if (p == NULL); //i值不合法return false;if (p->next == NULL) //第i-1个结点之后已无其他结点return false;LNode *q = p->next; //令q指向被删除结点e = q->data; //用e返回元素的值p->next = q->next; //将*q结点从链中“断开”free(q); //释放结点的存储空间return true; //删除成功
}

分析
如果i = 4…
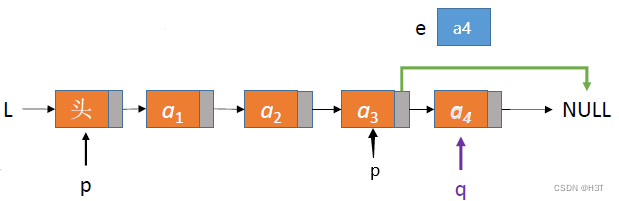
在这里插入图片描述

注意：此处变量e需要把此次删除的这个结点值代回函数的调用者处 —— 参数e是引用类型的

最坏、平均时间复杂度： $O (n)$
最好时间复杂度： $O (1)$

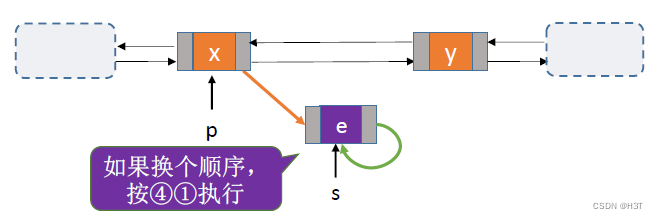
指定结点的删除

//删除指定结点p
bool DeleteNode (LNode *p)

在这里插入图片描述

删除结点p，需要修改其前驱结点的next指针
——没办法直接找到其前驱结点！

方法：

传入头指针，循环寻找p的前驱结点
偷天换日 - 交换数据（类似于结点前插的实现）

//删除指定结点p
bool DeleteNode (LNode *p){if (p == NULL)return false;LNode *q = p->next; //令q指向*p的后继结点p->data = p->next->data; //和后继结点交换数据域p->next = q->next; //将*q结点从链中“断开”free(q); //释放后继结点的存储空间return true;
}

在这里插入图片描述
时间复杂度： $O (1)$

Question：考虑一种极限情况，如果此次要删除的这个p结点刚好是单链表的最后一个结点：
——执行该代码时，会出现q指向NULL的情况

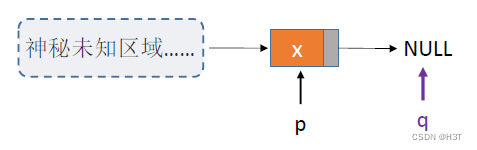
在这里插入图片描述
此时，执行(p->data = p->next->data)，取q结点的data域，会出现空指针的错误。

所以，针对要删除结点刚好是单链表最后一个结点时，只能从表头开始依次寻找p的前驱，时间复杂度为 $O (n)$

单链表的局限性：无法逆向检索，有时候不太方便。
——可以使用双链表

2.3.2_2 单链表的查找

按位查找

在这里插入图片描述
上一节中，按位插入和按位删除这两个基本操作中已经实现了，按位查找的代码逻辑。

代码实现：

//按位查找，返回第i个元素（带头结点 - 第0个结点）
LNode *GetElem(LinkList L, int i){if (i < 0)return NULL;LNode *p; //指针p指向当前扫描到的结点int j = 0; //当前p指向的是第几个结点p = L; //L指向头结点，头结点是第0个结点(不存数据)while (p != NULL && j < i) //循环找到第i个结点p = p->next;j++;}return p;
}

边界情况：

如果i = 0

跳过循环，返回头结点
如果i = 8

循环(p != NULL)不满足，返回NULL

需要考虑边界情况，使代码有健壮性

平均时间复杂度： $O (n)$

另一种版本代码：

首先把j的值设为1，p结点刚开始并不指向第0个结点，而是指向第1个结点。

封装（基本操作）的好处

既然实现了按位查找的基本操作
——那么可以通过调用封装 - 基本操作来实现一些步骤

在这里插入图片描述

封装成函数 - 可以避免重复代码，简洁、易维护

函数健壮性：
InsertNextNode函数中，判断if (p == NULL)是有必要的
——通过上一个子函数，p指针有可能是指向NULL的 - 【第i-1个结点不存在】，再向InsertNextNode函数里传入时，需要判断p结点是否存在(p == NULL)，不存在即返回false

尽可能提高代码的健壮性，多判断条件很有必要，边界情况是程序最容易出bug的地方。

按值查找

//按值查找，找到数据域==e的结点
LNode *LocateElem(LinkList L, ElemType e){LNode *p = L->next; //指向第1个结点//从第1个结点开始查找数据域为e的结点while (p != NULL && p->data != e)p = p->next;return p; //找到后返回该结点指针，否则返回NULL
}

假设本例中ElemType是int
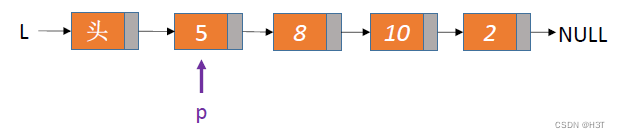
在这里插入图片描述
能找到的情况：

如果e = 8
当循环到第2个结点【8】
此时p->data == e时跳出循环，返回p结点

不能找到的情况：

如果e = 6
循环到NULL时
此时(p != NULL)不满足，跳出循环，返回的p即NULL
Question：如果ElemType是更复杂的结构类型呢？
——比如说对struct类型的相等判断就不能用操作符（==）
该点在之前的小节中做过说明

平均时间复杂度 $O (n)$

求表的长度

//求表的长度
int Length(LinkList L){int len = 0; //统计表长LNode *p = L;while (p->next != NULL){p = p->next;len++;}return len;
}

让p结点依次往后移，用一个变量len依次累加记录表长，最后返回len

时间复杂度 $O (n)$

2.3.2_3 单链表的建立

在这里插入图片描述
如果给你很多个数据元素（ElemType），要把它们存到一个单链表里边，这么做？

Step1：初始化一个单链表
Step2：每次取一个数据元素，插入到表尾/表头
——（本节探讨带头结点的情况）

尾插法建立单链表

将新的数据元素插入到单链表的表尾

思路1：

代码实现：
Step1：初始化一个单链表

typedef struct LNode{ //定义单链表结点类型ElemType data; //每个节点存放一个数据元素struct LNode *next; //指针指向下一个节点
}LNode，*LinkList;//初始化一个单链表（带头结点）
bool InitList(LinkList &L){L = (LNode*) malloc(sizeof(LNode)); /分配一个头结点if (L == NULL) //内存不足，分配失败return false;L->next =NULL; //头结点之后暂时还没有节点return true;
}
void test( ){LinkList L; //声明一个指向单链表的指针//初始化一个空表InitList(L);//…
}

在这里插入图片描述
Step2：接下来用按位序插入这个基本操作，来每次取一个数据元素插到单链表的尾部：

按位序插入代码：

//在第i个位置插入元素e（带头结点）
bool ListInsert(LinkList &L, int i, ElemType e){if(i<1)return false;LNode *p; //指针p指向当前扫描到的结点int j=0; //当前p指向的是第几个结点p = L; //L指向头结点，头结点是第0个结点(不存数据)while (p != NULL && j < i - 1){ //循环找到第i-1个结点p = p->next;j++;}if (p == NULL) //i值不合法return false;LNode *s = (LNode *) malloc(sizeof(LNode));s->data = e;s->next = p->next;p->next = s; //将结点s连到p之后return true; //插入成功
}

由于每一次都要把数据元素插入到单链表的表尾，设置一个变量length用来记录单链表的当前长度

然后再通过while循环，每次取出一个数据元素e，用按位序插入这个基本操作，每次都将数据元素e插入到第length+1个位置

伪代码：

While 循环{每次取一个数据元素e;ListInsert (L, length + 1, e)插到尾部;length++;
}

本例中
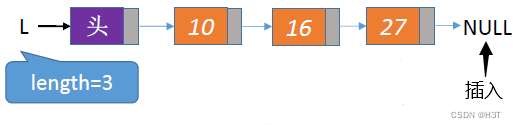
在这里插入图片描述

插入到length + 1 = 4的位置，即表尾的位置。

每次插入一个新的元素之后，都会导致单链表的长度length + 1

使用这种方法实现，每次要在表尾插入元素时，都需要通过循环从表头开始依次往后遍历，直到最后一个结点
——当插入第n个元素的时候，总共需要循环n-1次；
循环总次数为0+1+2+…+(n-1) - 时间复杂度为 $O(n^2)$

思路2：
设置一个指针r，让指针r指向表尾的最后一个数据结点；
那么在尾部插入一个新的数据元素的时候，只需要对r这个结点做一个后插操作即可

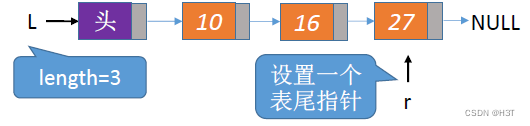
在这里插入图片描述

后插操作代码：

//后插操作：在p结点之后插入元素e
bool InsertNextNode (LNode *p, ElemType e) {
if (p==NULL)
return false;
LNode *s = (LNode *)malloc(sizeof ( LNode) );if (s==NULL)//内存分配失败
return false;
s->data = e;
//用结点s保存数据元素e
s->next=p->next;
p->next=s ;
//将结点s连到p之后
return true;
}

当后插操作完成后，还需要把表尾指针往后移动，始终指向尾结点。

代码实现：

LinkList List_TailInsert(LinkList &L){ //正向建立单链表int x; //设ElemType为整型
//初始化空表L = (LinkList)m alloc(sizeof(LNode)); //建立头结点L->next = NULL; //初始化空链表LNode *s,*r = L; //r为表尾指针scanf("%d", &x); //输入结点的值while (x != 9999){ //输入9999表示结束
//在r结点之后插入元素xs = (LNode *)malloc(sizeof(LNode)); //s指向申请的新结点s->data = x; //s数据域为输入的值r->next = s; //r结点next指针指向s结点
//永远保持r指向最后一个结点r = s; //r指向新的表尾结点scanf("%d",&x);}r->next = NULL; //尾结点指针置空return L;
}

时间复杂度 $O (n)$

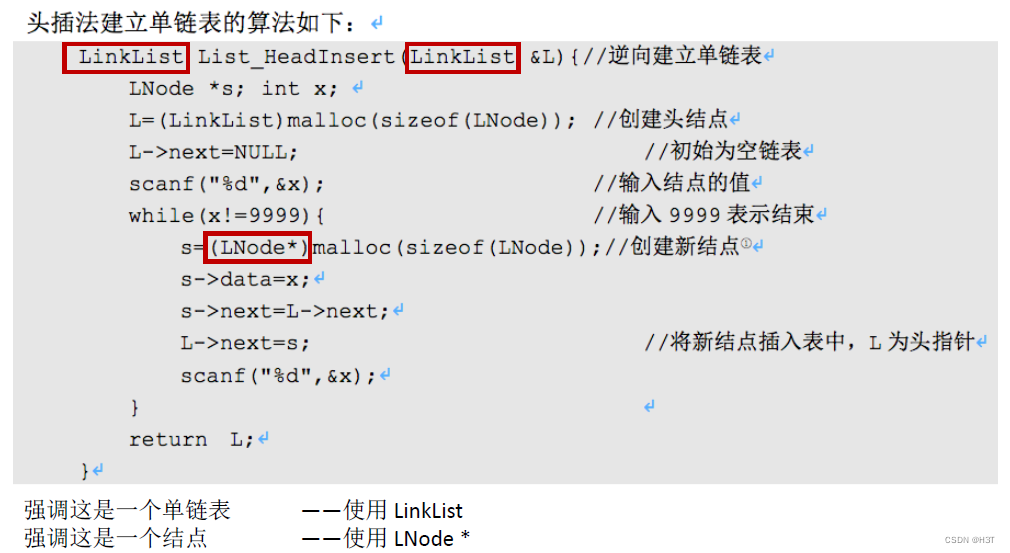
头插法建立单链表

将新的数据元素插入到单链表的表头

核心思想：对头结点进行后插操作

后插操作代码：

//后插操作：在p结点之后插入元素e
bool InsertNextNode (LNode *p, ElemType e) {
if (p==NULL)
return false;
LNode *s = (LNode *)malloc(sizeof ( LNode) );if (s==NULL)//内存分配失败
return false;
s->data = e;
//用结点s保存数据元素e
s->next=p->next;
p->next=s ;
//将结点s连到p之后
return true;
}

Step1：初始化单链表
Step2：

伪代码：

While 循环{每次取一个数据元素e;InsertNextNode (L, e);
}

代码实现：

LinkList List_HeadInsert(LinkList &L){ //逆向建立单链表LNode *s;int x;L = (LinkList) malloc(sizeof(LNode)); //创建头结点
//初始化单链表 - 先把头指针指向NULLL->next = NULL; //初始为空链表scanf("%d",&x); //输入结点的值while(x != 9999){ //输入9999表示结束s = (LNode*) malloc(sizeof(LNode)); //创建新结点s->data = x;s->next = L->next;L->next = s; //将新结点插入表中，L为头指针scanf("%d", &x);}return L;
}

如果去掉（L->next = NULL; //初始为空链表）这一步
那么有可能最后一个结点的next指针指向一个未知的神秘区域（脏数据）
在这里插入图片描述
所以初始化单链表 - 都先把头指针指向NULL

头插法 - 读入数据的顺序与生成的链表中的元素顺序是相反的
——重要应用：链表的逆置 - 尝试用头插法实现

2.3.3 双链表

在这里插入图片描述

单链表V.S.双链表

单链表：

单链表：无法逆向检索（不能找前驱），有时候不太方便
双链表

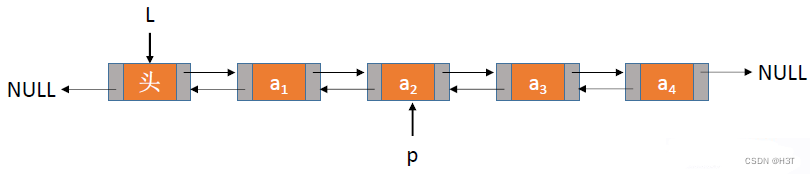
双链表：可进可退，存储密度更低一点

双链表结构体定义：

typedef struct DNode{ //定义双链表结点类型ElemType data; //数据域struct DNode *prior, *next; //前驱和后继指针
}DNode，*DLinklist;
//Double Node

初始化双链表（带头结点）

初始化双链表代码：

typedef struct DNode{ ElemType data; struct DNode *prior, *next; 
}DNode，*DLinklist;//初始化双链表
bool InitDLinkList (DLinklist &L){L = (DNode *) malloc(sizeof(DNode)); //分配一个头结点if (L == NULL) //内存不足，分配失败return false;L->prior = NULL; //头结点的prior永远指向NULLL->next = NULL; //头结点之后暂时还没有结点return true;
}void testDLinkList(){//初始化双链表DLinklist L; //声明一个指向头结点的指针LInitDLinkList(L);//后续…
}

在这里插入图片描述
判断双链表是否为空代码：

//判断双链表是否为空（带头结点）
bool Empty(DLinklist L){if (L->next == NULL)return true;elsereturn false;
}

双链表的插入

初步代码实现：

//在p结点之后插入s结点
bool InsertNextDNode (DNode *p, DNode *s){s->next = p->next; //将结点*s插入到结点*p之后 - Step 1p->next->prior = s; //Step 2s->prior = p; //Step 3p->next = s; //Step 4
}

Step1：将s结点的后向next指针，指向p结点的下一个结点；
Step2：将p结点后继结点的前向prior指针，指向s结点；
Step3：将s结点的前向prior指针，指向p结点；
Step4：将p结点的后向next指针，指向s结点。
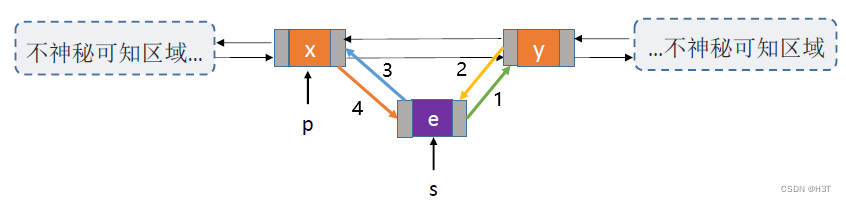
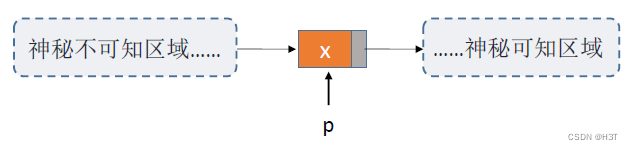
在这里插入图片描述
但是！如果p是最后一个结点：

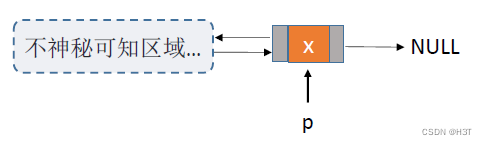
此时Step2：（p->next->prior = s;）中p->next为NULL，存在空指针错误。

严谨的代码实现：

//在p结点之后插入s结点
bool InsertNextDNode(DNode *p, DNode *s){if (p == NULL || s == NULL) //非法参数return false;s->next = p->next;if (p->next != NULL) //如果p结点有后继结点p->next->prior = s;s->prior = p;p->next = s;return true;
}

假设此时p结点是最后一个结点的情况：
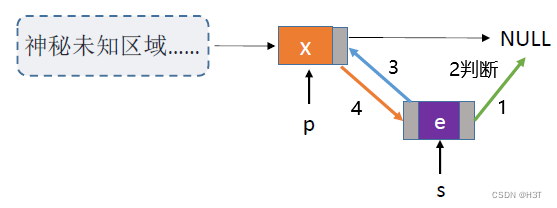
在这里插入图片描述
加入判断p结点有没有后继结点：（if (p->next != NULL)）
如果p结点没有后继结点，即跳过Step2，即可完成后插操作。

注：修改指针的顺序不可以颠倒！
Eg：颠倒Step1：（s->next = p->next;）和Step4：（p->next = s;）

就会出错！

双链表的删除

初步代码实现：

//删除p的后继结点q
p->next = q->next;
q->next->prior = p;
free(q);

在这里插入图片描述
和插入一样，当删除的结点刚好是最后一个结点的话，那么Step2同样会出现空指针错误。

增加条件判断，提升代码的健壮性
严谨代码实现：

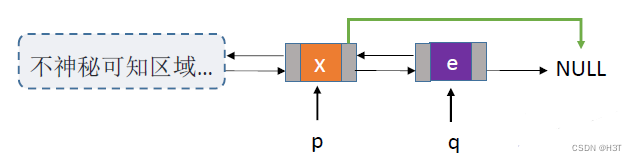
//删除p结点的后继结点
bool DeleteNextDNode(DNode *p){if (p == NULL)return false;DNode *q = p->next; //找到p的后继结点qif (q == NULL)return false; //p没有后继p->next = q->next;if (q->next != NULL) //q结点不是最后一个结点q->next->prior=p;free(q); //释放结点空间
return true;
}

删除p结点的后继结点步骤分析：

Step1：声明指针q，指向p的后继结点；

DNode *q = p->next;

Step2：判断 - 如果此时（q == NULL），那么说明p结点是没有后继结点的，返回false

if (q == NULL)return false; //p没有后继

Step3：p结点的next指针，指向q结点的next指针指向的相同位置

p->next = q->next;

Step4：判断 - 此时q结点还有没有后继结点

if (q->next != NULL) //q结点不是最后一个结点

Step5：q结点有后继结点的话，使q结点后继结点的prior指针指向p

q->next->prior=p;

Step6：释放q结点空间

free(q); //释放结点空间

在这里插入图片描述

销毁链表的代码实现：

void DestoryList(DLinklist &L){//循环释放各个数据结点while (L->next != NULL)DeleteNextDNode(L);free(L); //释放头结点L = NULL; //头指针指向NULL
}

每一次都删除头结点的后继结点，并依次将这些结点占用的空间释放掉，直到只剩下头结点，即这个表变空了；
最后再把头结点所占的空间也释放掉，让头指针指向NULL，就销毁掉一个双链表了。

双链表的遍历

后向遍历：

while (p != NULL){//对结点p做相应处理，如打印p = p->next;
}

前向遍历：

while (p != NULL){//对结点p做相应处理p = p->prior;
}

前向遍历（跳过头结点）

while (p->prior != NULL){//对结点p做相应处理p = p->prior;
}

双链表不可随机存取，按位查找、按值查找操作都只能用遍历的方式实现。

时间复杂度 $O (n)$

2.3.4 循环链表

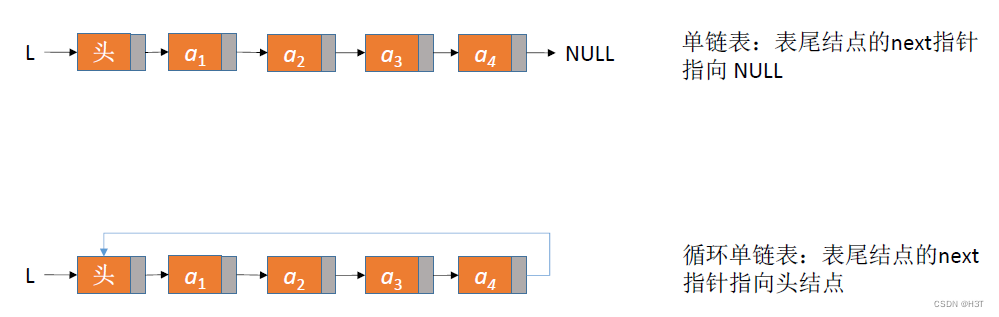
在这里插入图片描述

循环单链表

在这里插入图片描述

单链表：表尾结点的next指针指向NULL
循环单链表：表尾结点的next指针指向头结点

初始化循环单链表：

typedef struct LNode{ //定义单链表结点类型ElemType data; //每个节点存放一个数据元素struct LNode *next; //指针指向下一个节点
}LNode, *LinkList;//初始化一个循环单链表
bool InitList(LinkList &L){L = (LNode *) malloc(sizeof( LNode)); //分配一个头结点if (L == NULL) //内存不足，分配失败return false;L->next = L; //头结点next指向头结点return true;
}

需要把头结点的next指针指向头结点自己【L->next = L;】

判断循环单链表是否为空：

//判断循环单链表是否为空
bool Empty(LinkList L){if (L->next == L)return true;elsereturn false;
}

检查头结点的next指针是否指向它自己【if (L->next == L)】

判断结点p是否为循环单链表的表尾结点：

//判断结点p是否为循环单链表的表尾结点
bool isTail(LinkList L, LNode *p){if (p->next == L)return true;elsereturn false;
}

检查p结点的next指针是否指向头结点【if (p->next == L)】

循环单链表的特点：

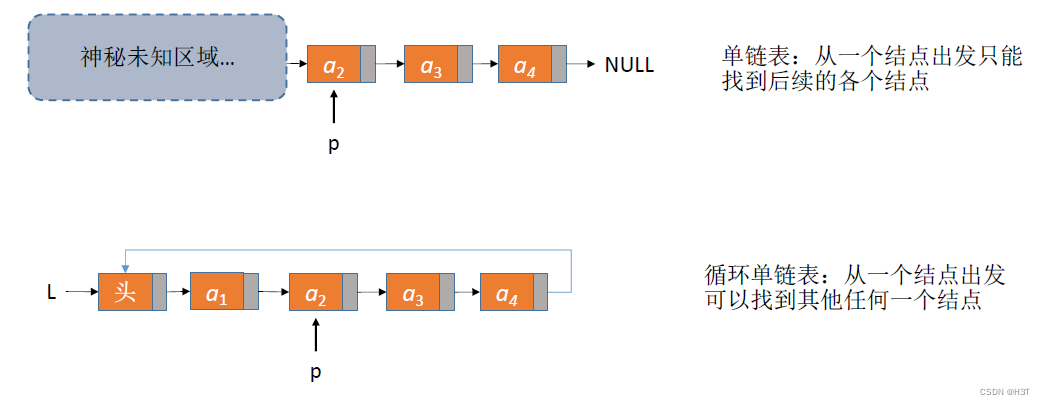
由于很多时候对链表的操作都是在头部或尾部（如头插法、尾插法建立链表）

从头结点找到尾部，时间复杂度为 $O (n)$

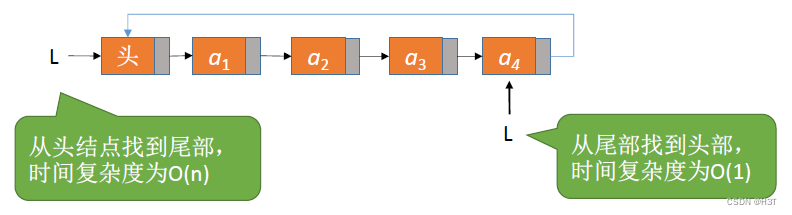
如果让单链表的指针L指向尾部结点，那么
从尾部找到头部，时间复杂度为 $O (1)$

如此，需要对链表尾部进行操作的时候，也可以在 $O (1)$ 的时间复杂度内就找到要操作的位置。【指针L指向尾部结点】

在应用场景中，需要经常对表头或者表尾进行操作的话，使用循环单链表时，可以让单链表的指针L指向表的尾部结点。
注意：在表尾插入、删除时可能需要修改指针L的指向

循环双链表

在这里插入图片描述

双链表：
表头结点的prior指向NULL；
表尾结点的next指向NULL

循环双链表：
表头结点的prior指向表尾结点；
表尾结点的next指向头结点。
所有的next指针形成了一个循环；
所有的prior指针也形成了另一个方向的循环。

初始化循环双链表：

typedef struct DNode{ElemType data;struct DNode *prior, *next;
}DNode, *DLinklist;//初始化空的循环双链表
bool InitDLinkList(DLinklist &L){L = (DNode *) malloc(sizeof(DNode)); //分配一个头结点if (L == NULL) //内存不足，分配失败return false;L->prior = L; //头结点的prior指向头结点L->next = L; //头结点的next指向头结点return true;
}void testDLinkList(){//初始化循环双链表DLinklist L;InitDLinkList(L);//...
}

需要把头结点的prior指针和next指针都指向头结点自己【L->next = L; L->next = L;】

判断循环双链表是否为空：

//判断循环双链表是否为空
bool Empty(DLinklist L){if (L->next == L)return true;elsereturn false;
}

检查头结点的next指针是否指向它自己【if (L->next == L)】

判断结点p是否为循环单链表的表尾结点

//判断结点p是否为循环单链表的表尾结点
bool isTail(DLinklist L, DNode *p){if (p->next == L)return true;elsereturn false;
}

检查p结点的next指针是否指向头结点【if (p->next == L)】

循环双链表的特点：

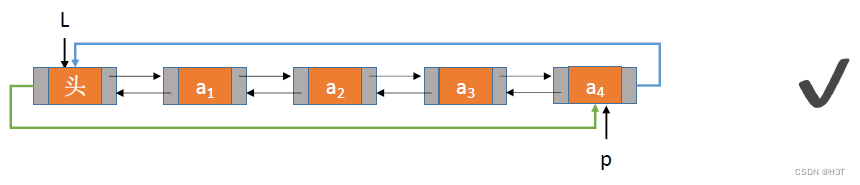
双链表的插入

//在p结点之后插入s结点
bool InsertNextDNode(DNode *p,DNode *s){s->next = p->next; //将结点*s插入到结点*p之后p->next->prior = s; //！s->prior = p;p->next = s;
}

对于普通双链表，当p结点刚好是表尾结点时，代码【p->next->prior = s;】会出现空指针错误，因为最后一个结点p结点并没有后继结点，所以也就无法做到修改p结点后继结点的前项指针。
在这里插入图片描述
使用循环双链表时，p结点为表尾结点时，它的next指针依然是非空的，所以逻辑没有问题。

双链表的删除

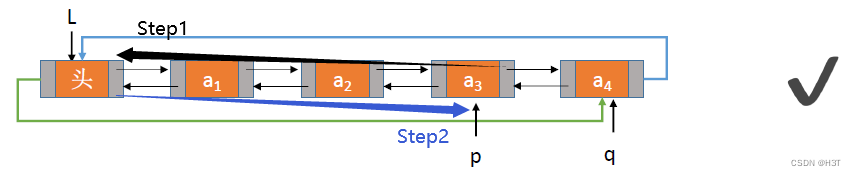
//删除p的后继结点qp->next = q->next;q->next->prior = p;
free(q);

对于普通双链表，当要删除的q结点刚好是表尾结点时，与插入时的情况一样，q结点并没有后继结点，会出现空指针错误。
在这里插入图片描述
使用循环双链表时，【p->next = q->next;】首先把p结点的next指针指向q结点的next位置 —— 即指向头结点的位置；
【q->next->prior = p;】把q结点的next —— 头结点的prior指针指向p结点；最后释放q结点。逻辑没有问题。
在这里插入图片描述

2.3.5 静态链表

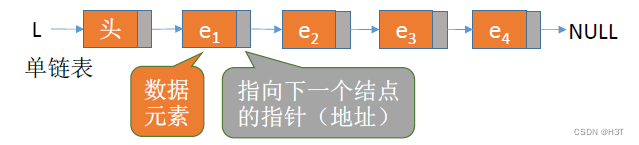
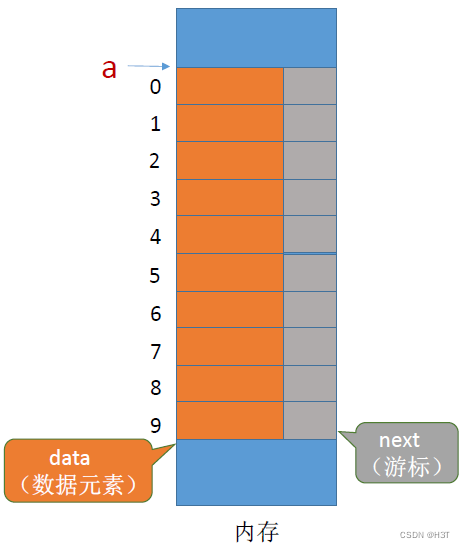
什么是静态链表

在这里插入图片描述

单链表：各个结点在内存中是离散的。
静态链表：分配一整片连续的内存空间，各个结点集中安置。

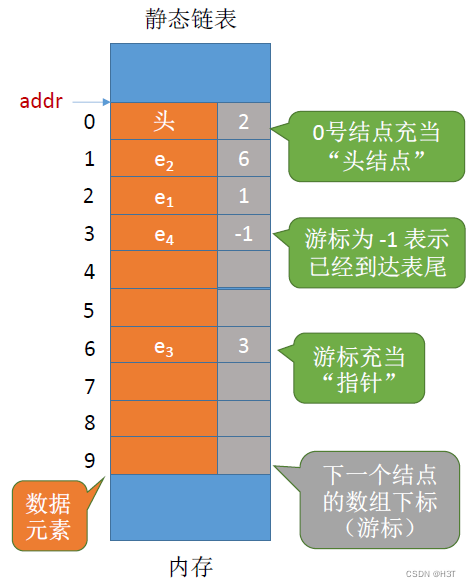
游标充当“指针”
指针指明具体的内存地址；游标指明下一个元素的数组下标

单链表中，表尾元素指向NULL；静态链表最后一个结点的游标值可以设为-1

每个数据元素4B，每个游标4B（每个结点共8B）
设起始地址为addr

数组下标为2的结点e1，其存放地址为：addr + 8*2
——0号结点的存放地址，加上每个结点的大小乘以接下来寻找的结点的数组下标大小

即，把静态数组中的数组下标（游标），映射成某一个数组下标对应结点的实际存放地址。

静态链表的定义

代码实现：

//静态链表的结点
#define MaxSize 10 //静态链表的最大长度
struct Node{ //静态链表结构类型的定义ElemType data; //存储数据元素int next; //下一个元素的数组下标
}；//通过数组声明静态链表
void testSLinkList(){struct Node a [MaxSize]; //数组a作为静态链表//…
}

在这里插入图片描述

另一种定义方法：

#define MaxSize 10 //静态链表的最大长度typedef struct{ //静态链表结构类型的定义ElemType data; //存储数据元素int next; //下一个元素的数组下标
}SLinkList[MaxSize];

这种定义方式等价于：

#define MaxSize 10 //静态链表的最大长度
struct Node{ //静态链表结构类型的定义ElemType data; //存储数据元素int next; //下一个元素的数组下标
};
typedef struct Node SLinkList[MaxSize]; //重命名

可用SLinkList定义“一个长度为MaxSize的Node型数组”
如果用SLinkList去定义一个变量a的话，即声明了一个数组，该数组的元素个数有MaxSize这么多，每一个数组元素为struct Node。

void testSLinkList(){ SLinkList a; //看上去a就是一个静态链表！！//…
}

等价于

void testSLinkList(){struct Node a[MaxSize]; //看上去a是一个Node型的数组//…
}

验证另一种定义方式：
在这里插入图片描述
运行结果为：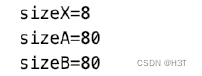

b是一个大小为10的数组，并且数组元素都是一个struct，其中包含了一个data和一个next。
——b和a一样。

结论：SLinkList b ——相当于定义了一个长度为MaxSize的Node型数组

静态链表的基本操作

#define MaxSize 10 //静态链表的最大长度typedef struct{ //静态链表结构类型的定义ElemType data; //存储数据元素int next; //下一个元素的数组下标
}SLinkList[MaxSize];void testSLinkList(){ SLinkList a; //…
}

初始化静态链表：
把a[0]的next设为-1
把其他结点的next设为一个特殊值来表示结点空闲，如-2
查找：
从头结点出发挨个往后遍历结点
时间复杂度为 $O (n)$

位序指的是各个结点在逻辑上的顺序，而数组下标其实只是反映了各个结点在物理上的顺序

插入位序为i的结点：
①找到一个此时空的结点，存入数据元素
②从头结点出发找到位序为i-1的结点
③修改新结点的next
④修改i-1号结点的next

Q：如何判断结点是否为空？
A：可让next为某个特殊值，如-2

删除某个结点
①从头结点出发找到前驱结点
②修改前驱结点的游标
③被删除结点next设为特殊值，如-2

2.3.6 顺序表和链表的比较

在这里插入图片描述

逻辑结构

在这里插入图片描述

存储结构

顺序表：

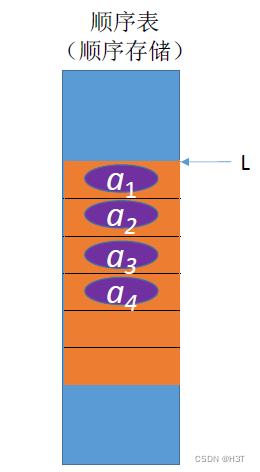
优点：支持随机存取、存储密度高
缺点：大片连续空间分配不方便，改变容量不方便
链表：

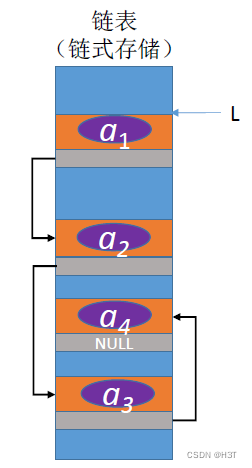
优点：离散的小空间分配方便，改变容量方便
缺点：不可随机存取，存储密度低

基本操作

创销、增删查改

a. 创

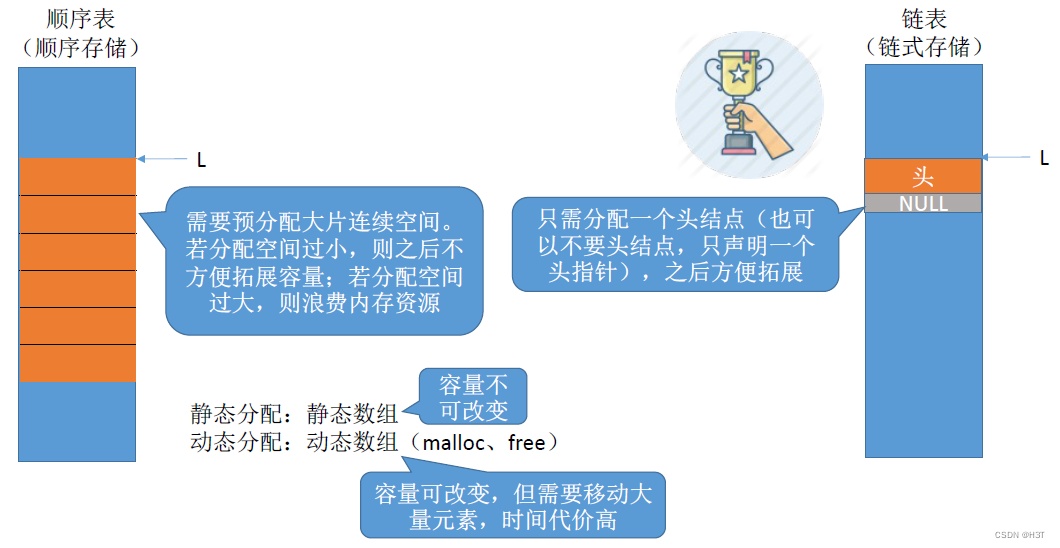
在这里插入图片描述

顺序表：需要预分配连续空间
过小 - 不方便拓展容量；
过大 - 则浪费内存资源
静态分配：静态数组 - 容量不可改变；
动态分配：动态数组（malloc、free） - 容量可更改，但要移动大量元素，时间代价高。
链表：分配一个头结点（也可以没有，只声明头指针）
方便拓展容量；

关于存储空间的灵活性方面，链表更胜一筹

b. 销

在这里插入图片描述

顺序表：
静态数组 - 系统自动回收
动态数组 - 手动释放空间，malloc申请空间和free释放必须成对出现。

c. 增删

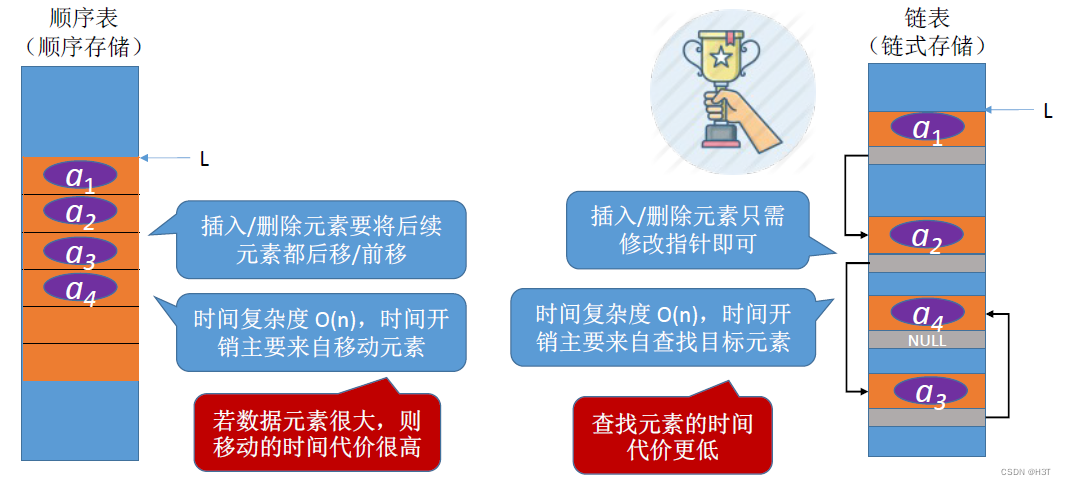
在这里插入图片描述

顺序表：时间开销来自移动元素
链表：时间开销来自查找目标元素

顺序表和链表的插入和删除操作时间复杂度都是 $O (n)$
但是移动元素的代价比查找元素的代价更大，
所以链表的增删效率要比顺序表高得多

d. 查

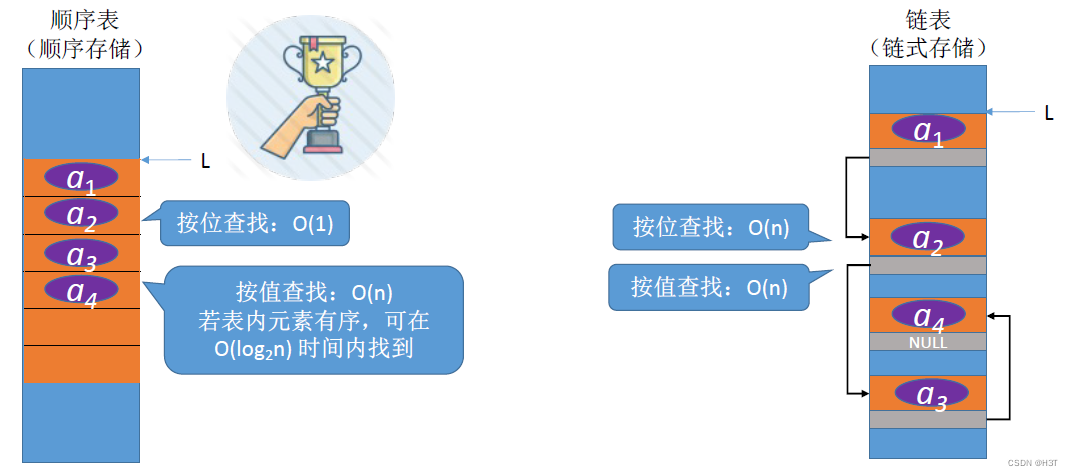
在这里插入图片描述

链表：无论有序还是无序，时间复杂度都是 $O (n)$

顺序表查找元素更方便

如何选择

在这里插入图片描述
表长难以预估、经常要增加/删除元素——链表

Eg. 奶茶店点单

表长可预估、查询（搜索）操作较多——顺序表

Eg. 学生点名

开放式问题的答题思路

Question：
请描述顺序表和链表的bla bla bla…
实现线性表时，用顺序表还是链表好?（6分）

Answer：

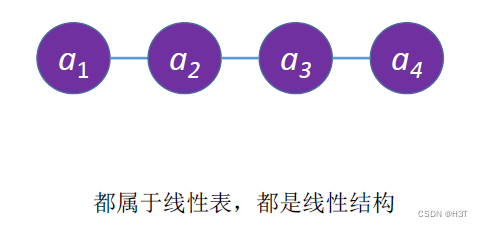
顺序表和链表的逻辑结构都是线性结构，都属于线性表。
但是二者的存储结构不同，顺序表采用顺序存储…(特点，带来的优点缺点)；链表采用链式存储…（特点、导致的优缺点）。
由于采用不同的存储方式实现，因此基本操作的实现效率也不同。当初始化时…；当插入一个数据元素时…；当删除一个数据元素时…；当查找一个数据元素时…

探讨逻辑结构；
探讨存储结构；
重要的基本操作，其实现效率又分别是什么样的；
得出结论，哪一个更好

知识回顾与重要考点

2.3.1 单链表的定义

在这里插入图片描述

存储结构：链式存储，结点间的先后关系用一个指针表示
带头结点的实现方式更方便
使用typedef关键字，重命名
“LinkList”强调这是链表；
“LNode *”强调这是结点

2.3.2_1 单链表的插入和删除

在这里插入图片描述

所有代码都要写，都重要
体会带头结点、不带头结点的代码区别
体会“封装”的好处 - 小功能模块化，代码逻辑清晰
指定结点删除中 - 指定结点是最后一个结点时，需要特殊处理

2.3.2_2 单链表的查找

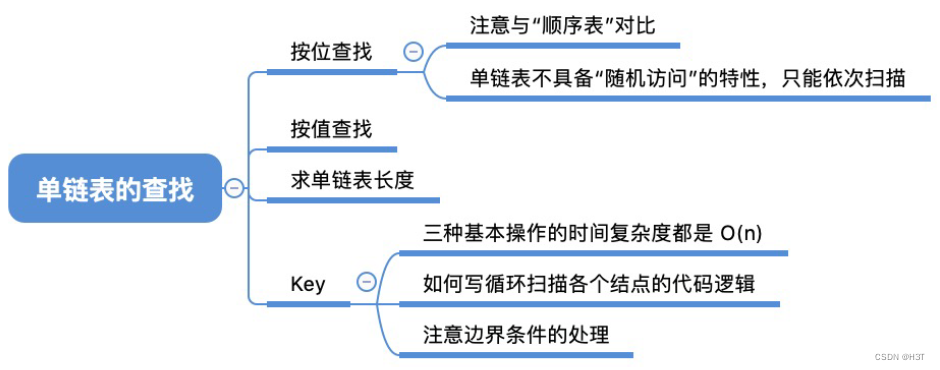
在这里插入图片描述

循环扫描各个结点
单链表不具备随机访问特性
查找都需要依次从头往后扫描
时间复杂度都是 $O (n)$

2.3.2_3 单链表的建立

头插法、尾插法：核心就是初始化操作、指定结点的后插操作
——注意设置一个指向表尾结点的指针
头插法的重要应用：链表的逆置

2.3.3 双链表

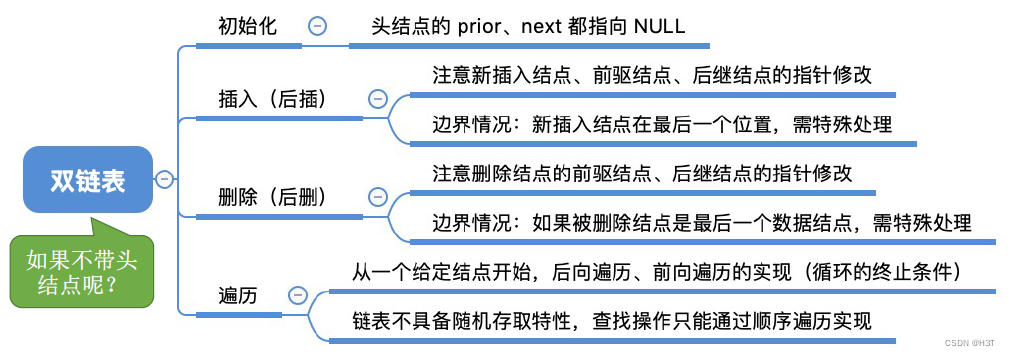
在这里插入图片描述

注意prior指针 - 初始化时prior、next都指向NULL
边界情况：插入/删除结点时最后一个位置/结点，需要特殊处理

2.3.4 循环链表

在这里插入图片描述

所有的链表，都不具备随机访问的特性，所以要寻找其中的某一个结点时，核心都是实现遍历，即循环，循环停止的位置就是表头/表尾。
所以判断结点p是否是表尾/表头结点 —— 后向/前向遍历的实现核心
在尝试插入或删除一个结点的时候，需要考虑该结点，在表头/表尾是否需要特殊处理，在表中如何处理。
考虑这三种情况时，基本覆盖了易错的边界条件。

2.3.5 静态链表

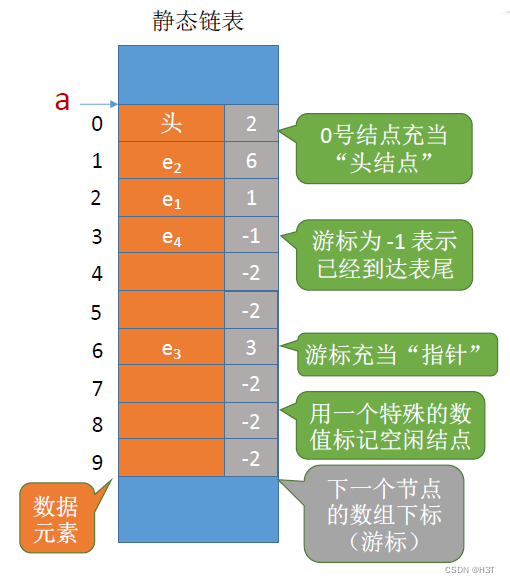
在这里插入图片描述

静态链表：用数组的方式实现的链表

各个逻辑上相邻的数据元素也可以在物理上不相邻；
各个元素之间的逻辑关系通过游标（数组下标）来表示

优点：增、删操作不需要大量移动元素
缺点：不能随机存取，只能从头结点开始依次往后查
找；容量固定不可变
适用场景：
①不支持指针的低级语言；
②数据元素数量固定不变的场景（如操作系统的文件分配表FAT）

2.3.6 顺序表和链表的比较

开放式问题的答题思路：

Question：
请描述顺序表和链表的bla bla bla…
实现线性表时，用顺序表还是链表好?（6分）

Answer：

顺序表和链表的逻辑结构都是线性结构，都属于线性表。
但是二者的存储结构不同，顺序表采用顺序存储…(特点，带来的优点缺点)；链表采用链式存储…（特点、导致的优缺点）。
由于采用不同的存储方式实现，因此基本操作的实现效率也不同。当初始化时…；当插入一个数据元素时…；当删除一个数据元素时…；当查找一个数据元素时…

探讨逻辑结构；
探讨存储结构；
重要的基本操作，其实现效率又分别是什么样的；
得出结论，哪一个更好

[入门必看]数据结构2.3：线性表的链式表示

[入门必看]数据结构2.3：线性表的链式表示

第二章 线性表

2.3 线性表的链式表示

知识总览

2.3.1 单链表的定义

2.3.2_1 单链表的插入删除

2.3.2_2 单链表的查找

2.3.2_3 单链表的建立

2.3.3 双链表

2.3.4 循环链表

2.3.5 静态链表

2.3.6 顺序表和链表的比较

2.3.1 单链表的定义

单链表的实现

使用typedef关键字 —— 数据类型重命名

初始化单链表

2.3.2_1 单链表的插入和删除

按位序的插入（带头结点）

按位序的插入（不带头结点）

指定结点的后插操作

指定结点的前插操作

按位序删除（带头结点）

指定结点的删除

2.3.2_2 单链表的查找

按位查找

封装（基本操作）的好处

按值查找

求表的长度

2.3.2_3 单链表的建立

尾插法建立单链表

头插法建立单链表

2.3.3 双链表

单链表V.S.双链表

初始化双链表（带头结点）

双链表的插入

双链表的删除

双链表的遍历

2.3.4 循环链表

循环单链表

循环双链表

2.3.5 静态链表

什么是静态链表

静态链表的定义

静态链表的基本操作

2.3.6 顺序表和链表的比较

逻辑结构

存储结构

基本操作

a. 创

b. 销

c. 增删

d. 查

如何选择

开放式问题的答题思路

知识回顾与重要考点

2.3.1 单链表的定义

2.3.2_1 单链表的插入和删除

2.3.2_2 单链表的查找

2.3.2_3 单链表的建立

2.3.3 双链表

2.3.4 循环链表

2.3.5 静态链表

2.3.6 顺序表和链表的比较

相关文章

第二章线性表