难度中等2119

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：

输入：grid = [["1","1","1","1","0"],["1","1","0","1","0"],["1","1","0","0","0"],["0","0","0","0","0"]
]
输出：1

示例 2：

输入：grid = [["1","1","0","0","0"],["1","1","0","0","0"],["0","0","1","0","0"],["0","0","0","1","1"]
]
输出：3

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 300
• grid[i][j] 的值为 '0' 或 '1'

题解：https://leetcode.cn/problems/number-of-islands/solution/dfs-bfs-bing-cha-ji-python-dai-ma-java-dai-ma-by-l/

并查集中维护连通分量的个数，在遍历的过程中：

• 相邻的陆地（只需要向右看和向下看）合并，只要发生过合并，岛屿的数量就减少

• 在遍历的过程中，同时记录空地的数量；

• 并查集中连通分量的个数 - 空地的个数，就是岛屿数量。

class Solution {int rows, cols;public int numIslands(char[][] grid) {rows = grid.length;if(rows == 0) return 0;cols = grid[0].length;int space = 0; // 空地的数量UnionFind unionFind = new UnionFind(rows * cols);int[][] directions = {{1, 0}, {0, 1}};for(int i = 0; i < rows; i++){for(int j = 0; j < cols; j++){if(grid[i][j] == '0'){space++;continue;} for(int[] dir : directions){int newx = i + dir[0];int newy = j + dir[1];if(newx < rows && newy < cols && grid[newx][newy] == '1'){unionFind.union(getIndex(i, j), getIndex(newx, newy));}}}}// 并查集中连通分量的个数 - 空地的个数，就是岛屿数量return unionFind.getCount() - space;}private int getIndex(int i, int j) {return i * cols + j;}
}class UnionFind {//par数组用来存储根节点，par[x]=y表示x的根节点为yprivate int[] parent;private int count;public int getCount(){return count;}public UnionFind(int n) {parent = new int[n];this.count = n;//初始化, 每个节点都是一个联通分量for (int i = 0; i < n; i++) {parent[i] = i;}}//查找x所在集合的根（带路径压缩）private int find(int x) {if (x != parent[x]) {//递归返回的同时压缩路径parent[x] = find(parent[x]);}return parent[x];}//合并x与y所在集合public void union(int x, int y) {int xRoot = find(x);int yRoot = find(y);if (xRoot != yRoot) { //不是同一个根，即不在同一个集合，就合并parent[xRoot] = yRoot;count--;}}
}

难度中等428

给定一个列表 accounts，每个元素 accounts[i] 是一个字符串列表，其中第一个元素 accounts[i][0] 是 名称 (name)，其余元素是 emails 表示该账户的邮箱地址。

现在，我们想合并这些账户。如果两个账户都有一些共同的邮箱地址，则两个账户必定属于同一个人。请注意，即使两个账户具有相同的名称，它们也可能属于不同的人，因为人们可能具有相同的名称。一个人最初可以拥有任意数量的账户，但其所有账户都具有相同的名称。

合并账户后，按以下格式返回账户：每个账户的第一个元素是名称，其余元素是 按字符 ASCII 顺序排列 的邮箱地址。账户本身可以以 任意顺序 返回。

示例 1：

输入：accounts = [["John", "johnsmith@mail.com", "john00@mail.com"], ["John", "johnnybravo@mail.com"], ["John", "johnsmith@mail.com", "john_newyork@mail.com"], ["Mary", "mary@mail.com"]]
输出：[["John", 'john00@mail.com', 'john_newyork@mail.com', 'johnsmith@mail.com'],  ["John", "johnnybravo@mail.com"], ["Mary", "mary@mail.com"]]
解释：
第一个和第三个 John 是同一个人，因为他们有共同的邮箱地址 "johnsmith@mail.com"。 
第二个 John 和 Mary 是不同的人，因为他们的邮箱地址没有被其他帐户使用。
可以以任何顺序返回这些列表，例如答案 [['Mary'，'mary@mail.com']，['John'，'johnnybravo@mail.com']，
['John'，'john00@mail.com'，'john_newyork@mail.com'，'johnsmith@mail.com']] 也是正确的。

示例 2：

输入：accounts = [["Gabe","Gabe0@m.co","Gabe3@m.co","Gabe1@m.co"],["Kevin","Kevin3@m.co","Kevin5@m.co","Kevin0@m.co"],["Ethan","Ethan5@m.co","Ethan4@m.co","Ethan0@m.co"],["Hanzo","Hanzo3@m.co","Hanzo1@m.co","Hanzo0@m.co"],["Fern","Fern5@m.co","Fern1@m.co","Fern0@m.co"]]
输出：[["Ethan","Ethan0@m.co","Ethan4@m.co","Ethan5@m.co"],["Gabe","Gabe0@m.co","Gabe1@m.co","Gabe3@m.co"],["Hanzo","Hanzo0@m.co","Hanzo1@m.co","Hanzo3@m.co"],["Kevin","Kevin0@m.co","Kevin3@m.co","Kevin5@m.co"],["Fern","Fern0@m.co","Fern1@m.co","Fern5@m.co"]]

提示：

• 1 <= accounts.length <= 1000
• 2 <= accounts[i].length <= 10
• 1 <= accounts[i][j].length <= 30
• accounts[i][0] 由英文字母组成
• accounts[i][j] (for j > 0) 是有效的邮箱地址

class Solution {// 利用一个字符串的映射存储并查集Map<String, String> map;public List<List<String>> accountsMerge(List<List<String>> accounts) {map = new HashMap<>();// 这个映射存储每个邮箱对应账户的名字Map<String, String> names = new HashMap<>();// 遍历所有账户构建并查集for(List<String> a : accounts){for(int i = 1; i < a.size(); i++){if(!map.containsKey(a.get(i))){// 如果并查集中没有这个邮箱，则添加邮箱，其根元素就是本身map.put(a.get(i), a.get(i));// 添加该邮箱对应的账户名names.put(a.get(i), a.get(0));}if(i > 1){// 并查集的合并操作，合并一个账户中的所有邮箱map.put(find(a.get(i)), find(a.get(i-1)));}}}// 暂时存储答案中的邮箱列表，每个键值对的键就是每个并查集集合的根元素Map<String, List<String>> temp = new HashMap<>();for(String email : map.keySet()){// 获取当前邮箱对应并查集的根元素String root = find(email);// 将当前邮箱放入根元素对应的列表中if(!temp.containsKey(root)) temp.put(root, new ArrayList<>());temp.get(root).add(email);}List<List<String>> res = new ArrayList();// 将答案从映射中放到列表中for(String root : temp.keySet()){// 获取当前根元素对应的列表List<String> layer = temp.get(root);// 题目要求的排序Collections.sort(layer);// 添加姓名layer.add(0, names.get(root));// 将当前列表加入答案res.add(layer);}return res;}// 并查集查找模板函数，这里用字符串替换了之前的整型String find(String x){if(!map.get(x).equals(x)){map.put(x, find(map.get(x)));}return map.get(x);}
}

难度困难163

给你一个 n 个点组成的无向图边集 edgeList ，其中 edgeList[i] = [ui, vi, disi] 表示点 ui 和点 vi 之间有一条长度为 disi 的边。请注意，两个点之间可能有 超过一条边 。

给你一个查询数组queries ，其中 queries[j] = [pj, qj, limitj] ，你的任务是对于每个查询 queries[j] ，判断是否存在从 pj 到 qj 的路径，且这条路径上的每一条边都 严格小于 limitj 。

请你返回一个 布尔数组 answer ，其中 answer.length == queries.length ，当 queries[j] 的查询结果为 true 时， answer 第 j 个值为 true ，否则为 false 。

示例 1：

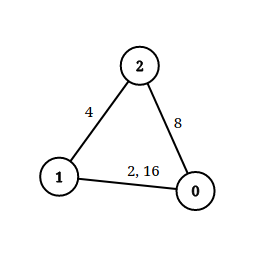
输入：n = 3, edgeList = [[0,1,2],[1,2,4],[2,0,8],[1,0,16]], queries = [[0,1,2],[0,2,5]]
输出：[false,true]
解释：上图为给定的输入数据。注意到 0 和 1 之间有两条重边，分别为 2 和 16 。
对于第一个查询，0 和 1 之间没有小于 2 的边，所以我们返回 false 。
对于第二个查询，有一条路径（0 -> 1 -> 2）两条边都小于 5 ，所以这个查询我们返回 true 。

示例 2：

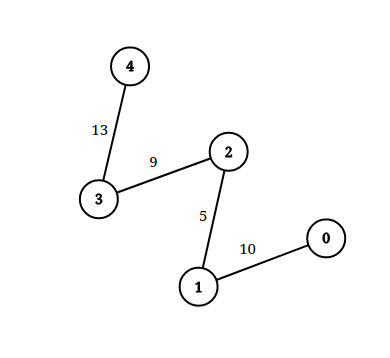
输入：n = 5, edgeList = [[0,1,10],[1,2,5],[2,3,9],[3,4,13]], queries = [[0,4,14],[1,4,13]]
输出：[true,false]
解释：上图为给定数据。

提示：

• 2 <= n <= 105
• 1 <= edgeList.length, queries.length <= 105
• edgeList[i].length == 3
• queries[j].length == 3
• 0 <= ui, vi, pj, qj <= n - 1
• ui != vi
• pj != qj
• 1 <= disi, limitj <= 109
• 两个点之间可能有 多条 边。

class Solution {// 题意：给n个节点m条带权值边的无向图。然后q个问题，每次询问点对的数目，//                              点对需要满足的条件是：1）连通；2）其路径的最大权值不能超过询问值limit。// 分析：如果每次询问一次，dfs一次，很可能超时，因此可以用并查集。// 离线处理，把边按权值排序，把问题按大小排序。然后离线的过程就是不断向图中加边的过程。int[] parent; // 并查集public boolean[] distanceLimitedPathsExist(int n, int[][] edgeList, int[][] queries) {parent = new int[n + 5];int m = queries.length, o = edgeList.length;// 初始化并查集for(int i = 0; i < n; i++) parent[i] = i;for(int i = 0; i < m; i++){// 由于需要将问题按大小排序，最后返回需要按序返回，所以需要将下表zip起来queries[i] = new int[]{i, queries[i][0], queries[i][1], queries[i][2]};}Arrays.sort(edgeList, (a, b) -> a[2] - b[2]);// 边按权值从小到大排序Arrays.sort(queries, (a, b) -> a[3] - b[3]); // 问题按询问从小到大排序boolean[] ans = new boolean[m];for(int i = 0, j = 0; i < m; i++){// 离线，将边长度小于查询limit的边都合并起来while(j < o && edgeList[j][2] < queries[i][3]){union(edgeList[j][0], edgeList[j][1]);j++;}// 查看两个点是否在同一个联通块上int a = find(parent[queries[i][1]]);int b = find(parent[queries[i][2]]);ans[queries[i][0]] = a == b;}return ans;}public void union(int a, int b){int x = find(a);int y = find(b);parent[y] = x;}public int find(int x){if(x != parent[x]) parent[x] = find(parent[x]);return parent[x];}
}

难度困难33

给你一个大小为 m x n 的整数矩阵 grid 和一个大小为 k 的数组 queries 。

找出一个大小为 k 的数组 answer ，且满足对于每个整数 queres[i] ，你从矩阵 左上角 单元格开始，重复以下过程：

• 如果 queries[i] 严格 大于你当前所处位置单元格，如果该单元格是第一次访问，则获得 1 分，并且你可以移动到所有 4 个方向（上、下、左、右）上任一 相邻 单元格。
• 否则，你不能获得任何分，并且结束这一过程。

在过程结束后，answer[i] 是你可以获得的最大分数。注意，对于每个查询，你可以访问同一个单元格 多次 。

返回结果数组 answer 。

示例 1：

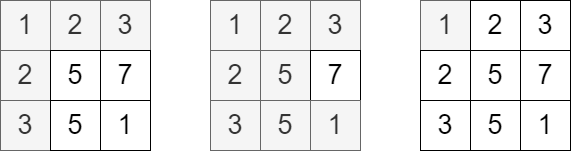
输入：grid = [[1,2,3],[2,5,7],[3,5,1]], queries = [5,6,2]
输出：[5,8,1]
解释：上图展示了每个查询中访问并获得分数的单元格。

示例 2：

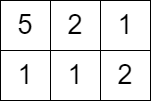
输入：grid = [[5,2,1],[1,1,2]], queries = [3]
输出：[0]
解释：无法获得分数，因为左上角单元格的值大于等于 3 。

提示：

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 1000
• 4 <= m * n <= 105
• k == queries.length
• 1 <= k <= 104
• 1 <= grid[i][j], queries[i] <= 106

题解：https://leetcode.cn/problems/maximum-number-of-points-from-grid-queries/solution/by-endlesscheng-qeei/

把矩阵的元素值从小到大排序，询问也从小到大排序。

用双指针遍历矩阵元素值和询问，如果矩阵元素值小于询问值，就把该格子和周围四个格子中的小于询问值的格子相连。

用并查集可以实现相连的过程，同时维护每个连通块的大小。

答案就是左上角的连通块的大小（前提是左上角小于询问值）。

class Solution {private static final int[][] dirs = {{-1, 0}, {0, 1}, {0, -1}, {1,0}};private int[] parent,size;public int[] maxPoints(int[][] grid, int[] queries) {int m = grid.length, n = grid[0].length, mn = m * n;// 并查集初始化parent = new int[mn];for(int i = 0; i < mn; i++) parent[i] = i;size = new int[mn];Arrays.fill(size, 1);// 矩阵元素从小到大排序，方便离线查询int[][] a = new int[mn][3];for(int i = 0; i < m; i++){for(int j = 0; j < n; j++){a[i*n + j] = new int[]{grid[i][j], i, j};}}Arrays.sort(a, (p, q) -> p[0] - q[0]); // 查询的下标按照查询值从小到大排序，方便离线int k = queries.length;Integer[] id = IntStream.range(0, k).boxed().toArray(Integer[]::new);Arrays.sort(id, (i, j) -> queries[i] - queries[j]);int[] ans = new int[k];int j = 0;for(int i : id){int q = queries[i]; // 限定值limitwhile(j < mn && a[j][0] < q){int x = a[j][1], y = a[j][2]; //将(x,y)点与四个格子连接起来，前提是符合条件for(int[] d : dirs){int nx = x + d[0], ny = y + d[1];if(0 <= nx && nx < m && 0 <= ny && ny < n && grid[nx][ny] < q){union(x*n + y, nx*n + ny);// 把坐标压缩成一维的编号}}j++;}if(grid[0][0] < q){ans[i] = size[find(0)];// 左上角的连通块的大小}}return ans;}private void union(int x, int y){int a = find(x);int b = find(y);if(a != b){parent[b] = a;size[a] += size[b];}}private int find(int x){if(x != parent[x]) parent[x] = find(parent[x]);return parent[x];}
}

难度困难23

给你两个下标从 0 开始的整数数组 nums 和 removeQueries ，两者长度都为 n 。对于第 i 个查询，nums 中位于下标 removeQueries[i] 处的元素被删除，将 nums 分割成更小的子段。

一个 子段 是 nums 中连续 正 整数形成的序列。子段和 是子段中所有元素的和。

请你返回一个长度为 n 的整数数组 answer ，其中 answer[i]是第 i 次删除操作以后的 最大 子段和。

**注意：**一个下标至多只会被删除一次。

示例 1：

输入：nums = [1,2,5,6,1], removeQueries = [0,3,2,4,1]
输出：[14,7,2,2,0]
解释：用 0 表示被删除的元素，答案如下所示：
查询 1 ：删除第 0 个元素，nums 变成 [0,2,5,6,1] ，最大子段和为子段 [2,5,6,1] 的和 14 。
查询 2 ：删除第 3 个元素，nums 变成 [0,2,5,0,1] ，最大子段和为子段 [2,5] 的和 7 。
查询 3 ：删除第 2 个元素，nums 变成 [0,2,0,0,1] ，最大子段和为子段 [2] 的和 2 。
查询 4 ：删除第 4 个元素，nums 变成 [0,2,0,0,0] ，最大子段和为子段 [2] 的和 2 。
查询 5 ：删除第 1 个元素，nums 变成 [0,0,0,0,0] ，最大子段和为 0 ，因为没有任何子段存在。
所以，我们返回 [14,7,2,2,0] 。

示例 2：

输入：nums = [3,2,11,1], removeQueries = [3,2,1,0]
输出：[16,5,3,0]
解释：用 0 表示被删除的元素，答案如下所示：
查询 1 ：删除第 3 个元素，nums 变成 [3,2,11,0] ，最大子段和为子段 [3,2,11] 的和 16 。
查询 2 ：删除第 2 个元素，nums 变成 [3,2,0,0] ，最大子段和为子段 [3,2] 的和 5 。
查询 3 ：删除第 1 个元素，nums 变成 [3,0,0,0] ，最大子段和为子段 [3] 的和 3 。
查询 5 ：删除第 0 个元素，nums 变成 [0,0,0,0] ，最大子段和为 0 ，因为没有任何子段存在。
所以，我们返回 [16,5,3,0] 。

提示：

• n == nums.length == removeQueries.length
• 1 <= n <= 105
• 1 <= nums[i] <= 109
• 0 <= removeQueries[i] < n
• removeQueries 中所有数字 互不相同 。

题解：https://leetcode.cn/problems/maximum-segment-sum-after-removals/solution/by-endlesscheng-p61j/

删除不好做，添加比较好做。不妨倒着思考，删除变成了添加。

添加时可能会合并两个子段。我们需要考虑如何动态维护每个子段的元素和，并高效地合并两个子段。

class Solution {//为什么不需要连接x,x-1?//合并都是往右合并的 x的结果会保留在x+1 就相当于已经合并了左边//ans[i] 要么取上一个ans[i+1] 的最大子段和，要么取合并后的子段和，这两者取最大值。int[] parent;public long[] maximumSegmentSum(int[] nums, int[] removeQueries) {int n = removeQueries.length;parent = new int[n+1]; for(int i = 0; i <= n; i++) parent[i] = i;long[] sum = new long[n+1];long[] ans = new long[n];ans[n-1] = 0;for(int i = n-1; i > 0; i--){int idx = removeQueries[i]; // 添加的下标idxunion(idx, idx+1);int to = parent[idx];sum[to] += nums[idx] + sum[idx];ans[i-1] = Math.max(sum[to], ans[i]);}return ans;}public void union(int a, int b){int x = find(a);int y = find(b);if(x != y){parent[x] = y;}}public int find(int x){if(x != parent[x]) parent[x] = find(parent[x]);return parent[x];}
}

难度困难68

给你一棵 n 个节点的树（连通无向无环的图），节点编号从 0 到 n - 1 且恰好有 n - 1 条边。

给你一个长度为 n 下标从 0 开始的整数数组 vals ，分别表示每个节点的值。同时给你一个二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示节点 ai 和 bi 之间有一条 无向 边。

一条 好路径 需要满足以下条件：

1. 开始节点和结束节点的值 相同 。
2. 开始节点和结束节点中间的所有节点值都 小于等于 开始节点的值（也就是说开始节点的值应该是路径上所有节点的最大值）。

请你返回不同好路径的数目。

注意，一条路径和它反向的路径算作 同一 路径。比方说， 0 -> 1 与 1 -> 0 视为同一条路径。单个节点也视为一条合法路径。

示例 1：

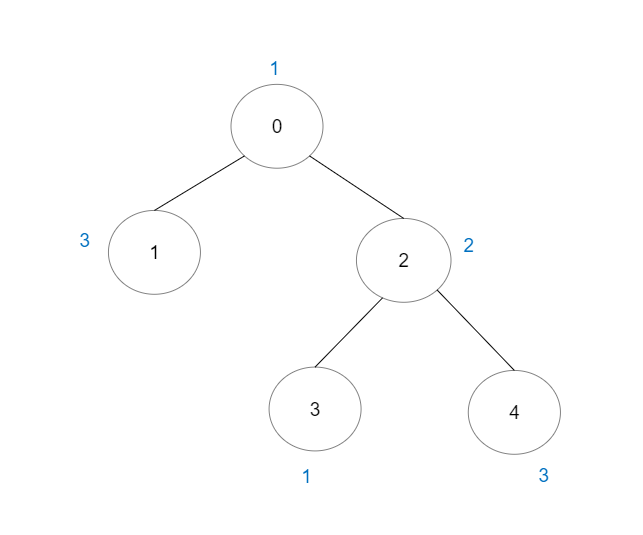
输入：vals = [1,3,2,1,3], edges = [[0,1],[0,2],[2,3],[2,4]]
输出：6
解释：总共有 5 条单个节点的好路径。
还有 1 条好路径：1 -> 0 -> 2 -> 4 。
（反方向的路径 4 -> 2 -> 0 -> 1 视为跟 1 -> 0 -> 2 -> 4 一样的路径）
注意 0 -> 2 -> 3 不是一条好路径，因为 vals[2] > vals[0] 。

示例 2：

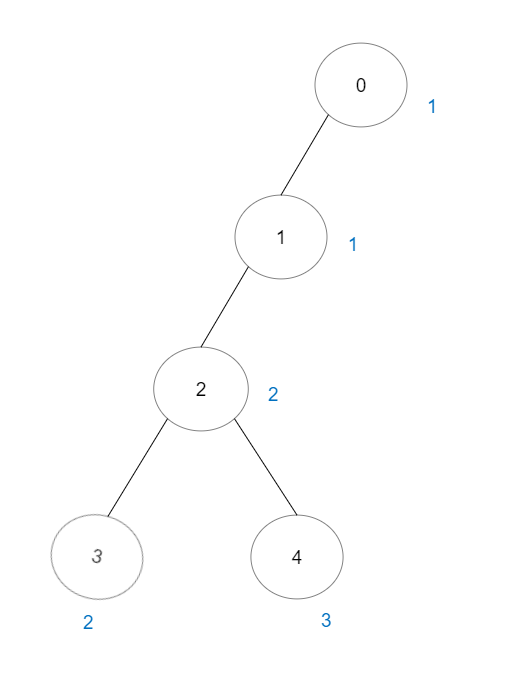
输入：vals = [1,1,2,2,3], edges = [[0,1],[1,2],[2,3],[2,4]]
输出：7
解释：总共有 5 条单个节点的好路径。
还有 2 条好路径：0 -> 1 和 2 -> 3 。

示例 3：

输入：vals = [1], edges = []
输出：1
解释：这棵树只有一个节点，所以只有一条好路径。

提示：

• n == vals.length
• 1 <= n <= 3 * 104
• 0 <= vals[i] <= 105
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• edges 表示一棵合法的树。

题解：https://leetcode.cn/problems/number-of-good-paths/solution/bing-cha-ji-by-endlesscheng-tbz8/

按节点值从小到大考虑，同时用并查集合并时，总是从节点值小的点往节点值大的点合并，这样可以保证连通块的代表元的节点值是最大的。

对于节点 x 及其邻居 y，如果 y 所处的连通分量的最大节点值不超过 vals[x]，那么可以把 y 所处的连通块合并到 x 所处的连通块中。

如果此时这两个连通块的最大节点值相同，那么可以根据乘法原理，把这两个连通块内的等于最大节点值的节点个数相乘，加到答案中。

class Solution {// 开始节点的值应该是路径上所有节点的最大值// 从大到小超时&有删除操作->反着来删除变合并->并查集int[] parent;public int numberOfGoodPaths(int[] vals, int[][] edges) {int n = vals.length;List<Integer>[] g = new ArrayList[n];Arrays.setAll(g, e -> new ArrayList<>());for(int[] e : edges){int x = e[0], y = e[1];g[x].add(y);g[y].add(x); // 建图}parent = new int[n];for(int i = 0; i < n; i++) parent[i] = i;// size[x] 表示节点值等于 vals[x] 的节点个数，// 如果按照节点值从小到大合并，size[x] 也是连通块内的等于最大节点值的节点个数int[] size = new int[n];Arrays.fill(size, 1);// 查询的下标按照查询值从小到大排序var id = IntStream.range(0, n).boxed().toArray(Integer[]::new);Arrays.sort(id, (i, j) -> vals[i] - vals[j]);int ans = n;for(int x : id){int vx = vals[x], fx = find(x);for(int y : g[x]){y = find(y);if(y == fx || vals[y] > vx) continue;// 只考虑最大节点值比 vx 小的连通块if(vals[y] == vx){ // 可以构成好路径ans += size[fx] * size[y]; // 乘法原理size[fx] += size[y]; // 统计连通块内节点值等于 vx 的节点个数}parent[y] = fx; // 把小的节点值合并到大的节点值上} }return ans;}int find(int x){if(parent[x] != x) parent[x] = find(parent[x]);return parent[x];}
}

e(0, n).boxed().toArray(Integer[]::new);
Arrays.sort(id, (i, j) -> vals[i] - vals[j]);

    int ans = n;for(int x : id){int vx = vals[x], fx = find(x);for(int y : g[x]){y = find(y);if(y == fx || vals[y] > vx) continue;// 只考虑最大节点值比 vx 小的连通块if(vals[y] == vx){ // 可以构成好路径ans += size[fx] * size[y]; // 乘法原理size[fx] += size[y]; // 统计连通块内节点值等于 vx 的节点个数}parent[y] = fx; // 把小的节点值合并到大的节点值上} }return ans;
}int find(int x){if(parent[x] != x) parent[x] = find(parent[x]);return parent[x];
}

}