题目描述

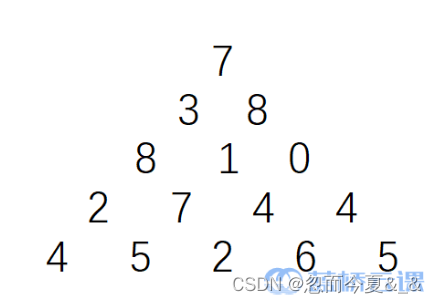
上图给出了一个数字三角形。从三角形的顶部到底部有很多条不同的路径。对于每条路径，把路径上面的数加起来可以得到一个和，你的任务就是找到最大的和（路径上的每一步只可沿左斜线向下或右斜线向下走）。

输入描述

输入的第一行包含一个整数 N (1≤N≤100)，表示三角形的行数。下面的 N 行给出数字三角形。数字三角形上的数都是 0 至 99 之间的整数。

输出描述

输出一个整数，表示答案。

实现代码

#include<bits/stdc++.h>
using namespace std;#define N 101int main()
{int n;cin>>n;int tri[N][N]={0};  // 存输入的三角形int dp[N][N]={0};   // 存动态规划算出来的数，到达每一个点最大的和for(int i=1;i<=n;i++){for(int j=1;j<=i;j++){cin>>tri[i][j];}}// 要算 dp[i][j] ，就得知道 tri[i][j]和 dp[i-1][j] 和 dp[i-1][j-1] 中哪个最大for(int i=1;i<=n;i++){for(int j=1;j<=i;j++){dp[i][j]=max(dp[i-1][j],dp[i-1][j-1])+tri[i][j];}}int ans=dp[n][1];for(int i=1;i<=n;i++){if(dp[n][i]>ans){ans=dp[n][i];}}cout<<ans;return 0;
}

解题思路

这个题是动态规划的题目，首先根据题意发现这个和递归很像，通过子问题堆叠可以推出要求解的问题，同时动态规划通常用于最优解问题，解决这个问题比较方便。

1. 把数字三角形存入二维数组，待后续取用。
2. 把三角形变成直角三角形，如下图，可以发现要求第三行的 “1” 的最大ans，就需要知道第二行 “3” 和 “8” 的最大 ans，取较大的 ans，因此可得到达每一个点的 dp[ i ] [ j ] = dp[ i-1 ] [ j-1 ] + dp[ i-1 ] [ j ] + tri[ i ] [ j ]，
3. 最后比较最后一行的每个数的ans，取最大即可得到答案。
   

注意点

• 注意 tri 和 dp 要开101个，不知道为什么，如果开 n+1 个的话，结果就不对……
• 注意 dp[ i ][ j ] 的算法，加完上面最大的ans之后，还需要加 tri[ i ] [ j ] 的值。

知识点

• 动态规划文章：看一遍就理解：动态规划详解 、 动态规划和递归的区别 。根据下面的代码可以更加直观地理解动态规划和递归的区别与相似之处。