Echarts 常用各类图表模板配置
注意: 这里主要就是基于各类图表,更多的使用 Echarts 的各类配置项;
以下代码都可以复制到 Echarts 官网,直接预览;
图标模板目录
- Echarts 常用各类图表模板配置
- 一、地图
- 二、环形图
- 三、k 线图
- 四、折线图
- 五、横向柱状图
- 六、折线图 + 柱状图
- 七、3D 柱状图
- 八、工程项目可视化
- 九、雷达图
- 十、象形柱图
- 十一、环形占比图
- 十二、圆环动画
- 十三、地图 json 免费下载
一、地图
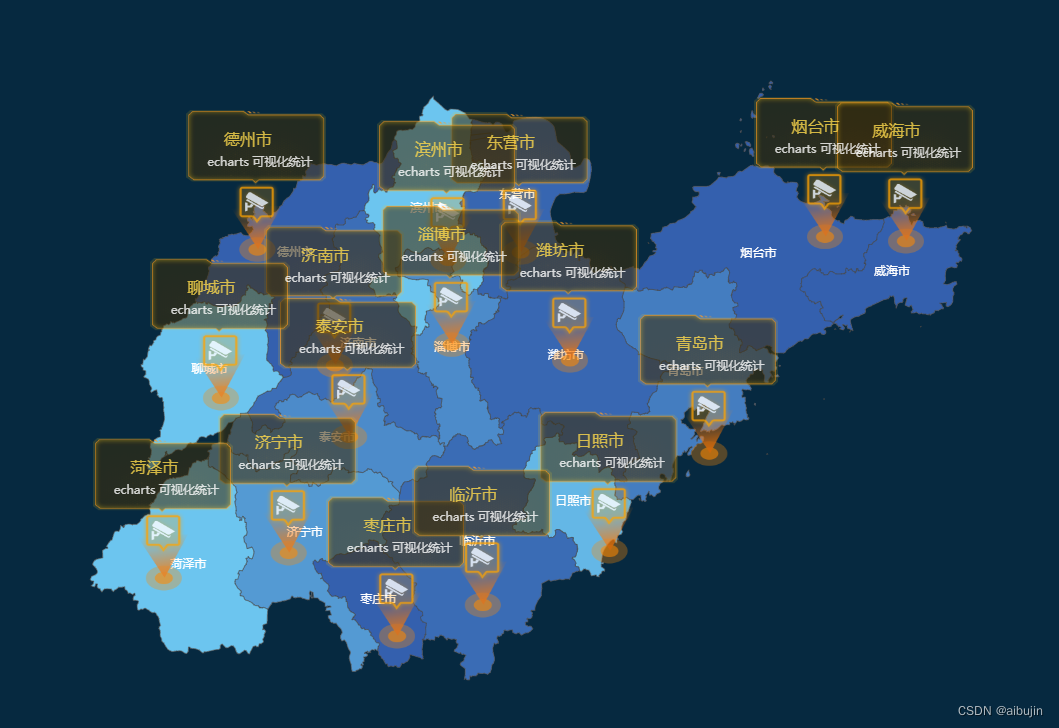
由于地图 json 文件过长,无法直接贴到代码中,大家可以 点击下载( 文章最后提供地图 json 下载方式,可自行选择 ),定义 var map = json文件,然后复制下面的代码,就可以在 echarts 官网直接预览
下面的案例用的是山东地图,拷贝山东地图即可预览
var map = 山东 json 文件
var iconLD ='image://data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAMgAAABwCAYAAABbwT+GAAAgAElEQVR4nO19a6xtWVbWGHOttfc591ZXdXUX3U0BUspDIbw6mGgiqFF8RiMGTEikffxEEkPQRIn/RY1Bo5I2wWBCm2gEY+IPxT8q0URNtIunCg3YNN00TVMWXVX3nrP3XmsOM15zjjX3Wvvsc+6tB1V3VW6dc+bea6655hzPb4w5JhIRtNfhxWffAwBfcPTBk2vtegkAPg0Ax5P55Hos1/DBl8/q5vDis4/0uPY5RwxyePHZ9wLA80+W9dbXFQB84vs/Mu5/k437yRWu7/q+V2d/9/GPI+YgwPHHL7+HdvhtTybxxIXwcnp2+p7uy3f/+Ts/1H/q+z8yfu67vuoDWwD4iwDwRwDgVwDgRwDgP1on/Nl9AHgIANfnPOLv//Svvhlv9o6/CoMsMMfV4b/f++6X9tOf/Dcff/gTr+7hcNhTnjJRBhC9kydastDethciQOqQf0ACwK5D3Gxo+LJnh/f8vv3FP7h3dflP+6+6/vB3fqj/LHz86jPw8uVPAMB3A8A3A8BfAoDvAYC/BQA7APgWAPg9APAAAP4tAPwnmzdmnPfz9Npnn32nE+mbeQmDHF589jkA+PwyDoKHh/9+76+8tJ/+3I987OHPvbLL+zED7XeUMyBNE1GeQDiFKeUdc2UATASpA0yImJCw39H0k7vDZz796vTwj79w79vf/9HLD3ZfvPvrhxce3IMXHvzP4cXnvhwA/qYxx/cCwAeNWZgp2GD+4wDwJTb//9r8mN8OAF9p2uW/AgAz2vQOo823xIX7j757iTn+6q9fT9/+wz//4Oc+d03762vIh5Hy7gB5PABBIsqErEZEf7wTtIioDf3JjAGQEfsBcOgBu4S4Gai7f5Eu/+AL2+e/5j3b1D83/fXuS3dM3L/GrDX872e+EUbW0LilZ3b/fvwtV5/h/oaPPfU7YErP8DTm91//1PTs/iq90m+7ly6ehwk20NF+/PzrX6aLaXyTp+Dtfr3y/R8Zx9YHYQb56vKXM8du+tAPf+zBz/4GM8cOpocPaTpMlA8HJNYkfI2uQd5BF5q27DtAFA0C0DODIKW+R9wOkC62uPnaD/TP/eEvvveFl++CH+i/8uoHoIN32Ez9prwYZPn48MGXZ4JoxiCH/3bvO399N337v/rFhz/38oO8u9rB9OAhTbsDTNc7yONINGWgaULKJKrjnQdrovogfU/yS9eZBukhDQNh32G62EL//Lu7p7/5Sy5feP7p/n/hQD/9Fhj5k6u58F35x7ov2b0YWplJ/u/wwZeLOdsyyE/+4M+++hMvPcjXDx7C9OCKxusDTLs9ZTWzQJx0MrNqmgLuj2/j6Q9ioBPtoSYXEiI77UNP2CXAYTBm2VDqEdP9S7z4hi8cPu+py24AImEs7HSi8O09Y2+JC8MMo1oAiOwhJEB2I7/y3Zt7w7P0F/qvuP7ZQMEzJunbF3ntAAc2o9jnYLPqeod5t4O82ytotd9Dbh2PTG//AFlCncBxZPBb/+iYMYhwmgCYMfYHRNYirGW7DvJ+ogf/9md3VykhMAP1CZAdfDHVCGWh3vw3e/tebhIzdTKgwmvYb1DWYTNg+pWr6d3fBJc/CD958W3911z/sjHJJQD81sOLzwqTHDEIQ7mMVrFDLj7HSCSag4iESViDZJyz5zvgmgkBUjRr2gOlhNj1gD0JdkFTRuR5YxPMzK/MfgrDwqkDSEk1CWsUZpIn1+t7ycQzPM8CitdjT8j+4mbI6WfG8WWCK/qmD1z+c/ipi2/rv/r6ky2THDGIxjmQxgOJQy4+R1bNIcxBKMTyDvQ+yiVkPakGyCNQzkSTM0oiyMYofLH5tT+oBuLF4nvYuacnzPG6XlE7o9mzLLD6jv1ESGwJTFOmn/r0QXJL/hAWJvlUZJIjBuEgIMc5RBySOuQsPMXvyMYcb5dZvONFNoM5swYBzJktWyI4MN8gMaNwDg9rkSmrr6KSTB18V75d94RL3pCLTaxO/T72E4cOxDLKTNtE8NOfObzMa/SHvqAwyadtWJdHDKIRcpA4x8gBQTJ3g/+H+IQ77PJpYCbhn2w5scZl0yuz6YWALFxSb7M2KkPMHMcnob835mLSZQWe2EKCdEhE2y0Hs0jUOfsnP/Nrh5f7gdI34b1/CQDf6OM61iDsbGguicY52FyYnmSprl1Rm4AxCtnfzCy4t3YEdAffryfq4425opCaCKhLzCokcCTu2BzDadgQ/p+Xxpe/6f2S1VCuYw1C77D0kcdwufSIjCLXVJGq7Hbqk+sNvVhIwV7hEBZSDJFs+px3+ySf9R3ilCkxEDWOeLRCRwziV2tKvROg3Ee9liZoMoZ5oi3epGvSmVdfkV0HhkcwMT7PlhFnhDA6y7AvhzbaQa4yyOx6srqPfD2RLm/uVTR7RpxGIOqJxjERm725JxAwamGRnhhTK9eSTMATsmLts1P3PLneuCvSvvmIYiWJ5YsG1S9YSedpkLfJFQm1nQls2mmhnc74/ql7/LObnn3OZ7dtv+s9b6er2Lqk0ApjvGJ2ZRRAigGq9nXfURqEVogWHmP7qb7gls++6bNz+3+U579dL0dmi9exwgm/6TTIkgR+PZ4Bd5Dad7nnrpL+HG3WjuvUPee23+Wet5rGMsCpvJLrjSUf5C3FIOcQ/7mTutbXoxBfnNWWYHCBMG96RtvXbcy1u7YvPee273gu451rdr4p15mO4VvGxDo13rs4xrd9xk3Xufe237sNQTxOZ/43EzDwVgYy3lQNcq4z+7gl51r7KYnaStZz2tf6gjP6OndcS++y1lerVU8BBnd9x1PjbZ9x0/q+Fa43RIPcVkLcVVqf89lNfWPz+10lW3vvo0rJc/s6p/2c30/1tTYOPKP9Nv3f9buP83rdGARXJMhd22+jOVppBytScK19zXe5TV9wQgredVxLfZ7StLdpb8d8qq9TWm6tr1PveC5NxPG8UdfrxiCnbO9zVOpNaru9lqRq2+dNhH9qTC1hLH3/1MKtPeO2fbXjfZRx3WRi3bb9tu8IZ9xzivHeiOuxMchNav+UJGg/u80itQSyZGffdM+5fS21rzHhUl/tdx5HX49zXO11Tl/t828zrrU1WaOVpf4f1XS96XpkJ33NLLlJA5ySgjc5h7BC+O2z7yIFX8++2u+8VfqyLfalzlm8Rz47s/3Uddd59GuNgV5vbfJIGuQcFXrquuvLnTKdzpV2p2znm55bmN0Ja6V96Vq759zxPuq4To2tveJ3FzXAQl9Lz7jLmpxa0/KsM9se5bq1Blnj3nM1QHzh22iNc7TJWp+36QtWJCqFyibg247Js3qMMOq+D1rry3+2fcVxxL7iONck/aOOi85o92fgLe7BMK67rEm8bqKVNRPuUTXMmxIobO1GhGVihzPab3rOW7GvtXE+7r6iJL9tX37vmsa5jSZqxxe1zDnvvkYra98/p/3c6zwNQlZogO6mNZak9No9d2m/YejlnhRNhtauvqVExaYv/2yt/S59PY5x3eUZ/Lf/9M9Ptd92XK4Zo5ajBU26to5rmqalocfhn5ynQXA5kes2dnz7MqeI/Lba5Kbnlufbot1EzFHCnWKk+PPU92+Swmt9xbEtjfcu41p6x6V+lp5/6tk3+SPx+dH0m43J72ufv7Lmral+yoS/67XKIFJLaOHTm1QcNgM9R/W198TrXAf4pkUSKRXHdYMJMRtDQ2ztoi/11RJR23ZuX2uMcNdxQSDOSKCRSKNU93uS3dNq4VN9tWM+OV9xbO14m9+XtEbLJHcRpkvXyT3pJVe+MbHah58r6U8N9tQ9EVK8i/nhi906mq3J0PYP7SKeuCe2FwJr3qUQ1wqR0UpftPLedx2XOOyBSCNxxTGn8J0lU9XbZ8Qd+mrHcWq8eMM6tjQBDa2cMtPb797memxO+k0a4KZrpo4X7l0iuLPHdgNev2RCtBJ1qY+bJr01a9aeeVM/s4V3pn+EcbV9nTNm9xH859L3Z6hfS+yPyeS5K33d9VrVIDMTK/ggrSm15jjFn074EbaEFQ1AZ8CW7T1rfcV2/2xVoobFTmG8OUi5qAHIpPCadF5qzwvaDOyzU5L+VF+nxhUl/am+KMwPF+GWdweajUtMLKmNTmf11Y6rfUcf1ylzbHEdV5z5m+ixEbZnc9btUKymKMrjNLGWvuOmVTSxoP38hPlxk+ZY62/p77XPolkx+3vt+81n/vfs55l9rY1r7Z7Y7iUeEQjDYFbHVfvBek9hjtN9tfPl/UfTrDXDTl23pbv2ebe5bvZBGo9IKpDeYPM9Dkm/NLFrCFR7TytRj3yQFYkKHlALY/R7yDVgqwFW2hclV/g93uNSmx+41tfaeJfGJQS70JfbsFqgvCrzUg+VSD5LZs6mQvh6TzLt4ePVcc0rmWN5leV3gZV3iZr8XFqhE9Dwmjax+8ofS0BUvG5GsRp2PJd7zyHmmd9xS3jyFNTohNlKJTcBouMW+5q1+1jDmJcccEfE2kUuz/eFauzzNLunTtZNz0jNu7d9kRHnUl+OcaNUTsOwVlSeUxgstPP4CoPZeOPnbV+1/fhdcjuPtiZ5gSZW17fxEeEGemw1RzSxbjpGcJlB1m6i5T8pvMBMEzQvCA2hHHV/BjwJraRooMaWeby9hSdT09cSQ7WgQQovGJ1Wb0/VwKiEWyamEgnG9kYIxL5iu5syd+0rronOiRB9ePdC1PYZ//+4vSvKhopPiVbntvRVxnY8X3CKqM+AjNurFYywwBBwQ/upa9nEimxzotcZly6ZRTdohtZhK49ccFqjSj6SQs0wZyZWkCJrsKVLVAjSsfblC0/ymd/TVftj1u5M0Xlf1p8TuL/gUl/d69AX/+k/EVwjgNg4ZPc5o3B7Ju2bP+tLXWE+k1KZIPYlFewX+vK/o2bycfE8rq3JEvxMJ2hlCSmDJcZbaQeoB+ysXSctsFPqh2BZHRIca4lznGVceYFzrtbkaJ9NMwbFxfajd1hqOwGBtu3Y9EAuadv2YirQYl/tPdT0RU1f8ftKQHNzCJp3a9dxTQovmClBoNFcc8D875vWpL2WTKilfk6N75Q2iT7ITdeyBjHGWPJB/Jpph1tke8afazDg3eFUPIIno+Tidnc0i63NUjCrgIqmFJjtXaSz9WXmBLozm0O7HHGQ7RmlL5tSktL7VdKjz03si2Z9TeTSHmaSfgp9QdPXmLUP7pM1gM+DS/pcJD3JLE92iphBuKY15Ik0yrj0Hm/nMYyizlSrJNTzNfj5oxSHrjTSVdo5mq+4Jq21gAEyXrM8WtrChRyvQo+NL9L6IKfOvLkZ5l24ecnOX/vOmsO11jbzAfR/t4ItYSViXe5R82DWHpGf+myqk8xEIK9CR/ekM/qqn1WzKM5RQj2WTZuozl0wWfRDfVYyF4S/6wQ5Q6uMwdpnu29hgyjvZt6GfaZHmOCM+LGkqVLwO1Jjm7Sm39K8tPPVrmNsn/2sD5mZ4vH3s0ysVn3CaRPrpA+yZmItcfVs70IDzR75EwFRWoMB23Zs4MEIW7qkLxOyAFtGydWhSruZNjHCmILYqpJeA0FjgUCptKNJVJfa/DNK5yhRXdLyGZByyp1JYbf167i0vUMnINK+AM1kIjk1F0zJntcX2VklBFzy3/vyAy7Bjmrgezqbh6FzhiTVjEGbuA44SAlP81HCO06mtXBhHpfWBA1KPgfKjvS1RHewok0C/doNAeZdofU7mVgFnmvRotB+pGWCuVQJpjI1BSaYOeaNM12eA3MpFc2iJdgymZPN35uoapNkppU7ljDzU6g4rUJkZv60zqwzGH9uhFLc5mgWsbOr9zvxk5o/QnzaZ5TaMt5ZX5Xxqrl6fl9sfx73VdyU4pjz6/MxfFNG4u9NxhzelxG4Lab2xX/6O+rcV8RrCvMVIePUAB+tiVXh6RP5aifoEZbId+2A5hVv/OZcrMZSWDKPAI5VYmzHBWerhVMjDNjCqeUeNwlWYEs3i+KQK2xZndYCgQYCjn3pmdqEKRhV3o5mDkUnsDNb36VnQXVQT5jSk20N2TEJkYwQuzSPd3SJrL36RMaEavqgE1o1vU71xff1qZo13pf/077QhBrafGlf2eaK7+tDX/6MHMYlYwjPcMJ1hPDUmiyt7xGUvUJ/a3S31taaWDfFQW6GeesAMQAWRwNYMqXWneljaHbuuK3Dlj6jCMfwZOnLLSxgbVGhTndaE+niQtEA6AfNm1lU8yLdOeUnR+msffFhwHqPt3eoZ6GDmSzxSDY+p5v7yrlKZ34WmzJo0x7bnSg7cYCxMDcTl/c1NX1tilnU9GXP8L5y7CvJa0ibOuxw1BebUso0x+PKWVnCGRvs2dn6J5o7/3FNIvDRri9GqyCS50qmREuPZ6GnN5hYjyWb95yBnLpn9nujNWbw5BosuPC7Ttr6sKKkXYVAzUbH4Ci33zl+Ps7u97YiVRtzrnm/Wft8jmj2DFcm8Xnuh5mP3fZV72n68ntEkwDOnlf6WhhHfGaMe7R/n0scLR3c9J1Hvk44536d9kHc8df5vRFuK37DDdCsf7/4DUAFBqS5M41tDpAr6yUIFOX7agsnG4ZLLv6fOKBJnUTTANgllY5qZpCZFwZb2hl2qh0Ihs7GTuoAuzPbJygSdT8RY7zkNrf2RSJpD5PZ7kSw6Uw42fO5D+5z0ykR86H3uwkyBg3F88H/HTLkQ8bsJt2QqPS1176g7Ws/QQY9Blk0AR9eya+y58MrMx9MBkd9mdaY9cXnje/DeDsz7TrTMlN27etaTs7XX4SMdU0qxJ2K+YpH+WJuot4YEohm903ZG/SI54PQDcy/NoCb/BFoJES1V9ch2CN4sIna1mdg8UlsUovqLQhTwoJAUXBm2/d1E06Y2aDOiMoI+pPnUs/bsSyVj1dRJOkzq8AxF6AwWG8+REoI2ZhYGL9TKc5/MOe5OWhP1bk2WIjvEUayBUfrq7N2oWS/M6vDvNZXF8Z19I5NOxQh5X5YdJjnkLGvCc9meBfLAaOy7vGZ7tN5LlkL4kQau1W9rhtsqEfyQeLnUWuczNycIUTHKBR65qhJiiJtRFo3qROosYmJDE5VV6FAoHLGu2kT1QBkmolQ4EnTNgyBmimFrDEoRx/EGVPvca2x6ZzpRDoXiSpEbWg9S3l3zKUvIx5+lktnlujbQZeJ/7c7SOhKPudnpKQztmNJP5E41Ek0n/lsmYi1Q89Q7AR0YX3x61wfKA/W17aDxIzHY+O+3Bfidy57QCYi0Uxk/kyvlMALwdps6KCMS/gWRZtkKqjZPJhZtS/7XxUyPkyQ55pc+2JtgraM0QcpkfoCsCxD/214Yc1fXrxuC/NiYMxTJtZRjOOGDUAesY6mlEOzbkDFwNlkEj4XG57i38Wd7wKWX+FUKBCoRIYnlaQFtrRT/8Uxrf7hzMRyp3Vy4jcNwCYTf49NCokxmESV73f1VFV1gEm+P5ETjDrmTPwsTfn4YR+XSHozJfme3t4Dxcl3swjzlOXN5fmbjpJoFyLYj5T5mWw2sUmoc0zCrANQmgwtEm3KxJq1L7CcKzaxuK/DyOMCGZeMI1Hpy/4Gj8DzPLiJ5aJFmQKM8dT0KmsSNLnHcNpcrph7FgVoDrlcRyGBJryw5A6sMspdYF484cYcmU/Nz6P2Begufic6yy6FUtOZ+xmGu8/g1AiBRpOrQqCVMQucGp6h7RXmjIvl4+/sMZ2uaHGqmSBNouquOzPGZJwstY0gIpTdmWbge92XyhKcQ9FAfarKX4WJaib5J8iUyLGiTeSeDtEyseRdemsflH3U5CYsfTmh+vO9LwSHjCs8y+PS8TraaKhdItdyWKF0ZRyfR58vKO+uULb7UN6f00ibr9bSU5zHVbo7oTFmwv+uMK/xb+G6aGItOUiL0e9gIxYNsBLQW4NmXQM4BJugdYChQJ0+sS65RNIbPMnfGdQ0gK6BLT1egBoxzhEydqeVSY+lrWsNl9piroX23giGb1ENVIG4Te/mD0t6KFrjclDPoE9AMw2QIDHB9uJ8U1bHVbftbTrt6zBR5s86zQPL2hfPTdNXz+EYsL6g9KWaT/sac+2Lx3XRw6yvMo9JzTX+Ww/fD+aarT33FSFjN2+xNb1CjpeOaa5NwLOPVzKD1+gur2gTqP6R+VvW+HrAvKtQXPz9DOhudm8DI1bY0ZLXlmI/DbwIAU6Nzy4R4+ZeC1KZuXf8bIgH0Veb2N3wGRQd74/xlPnv82dk6yvn6q+4Jigw8xwWX3yemiYVyZmPn8p+2DgWI2J5RtsX1XFRHFeGuKZhjnkeUxx/9SHid+YQe92n+6j0RCvtq9dpr0SuRQ1SfdZlmDfafDcVCDi11XMt07WFASE4dB6EY8gUsucTYTGZBFI0ODUrnCrfZ+0R4VT+OwUIVB19cYChK7arOa1mhmwHMP+bBOpsHWDu+/rAkCmVIJ2bJIdJtUYyraXSWUxAYsfcx3c5gBgzfQfd1QEnNth4DNz3xnyQq5HybqTsJs0900CYILFjzhAyvxNrE75l00H34AChLyow745Ua7jpcmF9Md3yu8RxuTaRd7R3Z20t75jU+VeNolcLP7cAhwcgK1hi/iIeZwYHc/soJODI1jkOe7HGLUfzTjDvEmyLlmlKofrOOTlTtc+61ROKFK6beDz1I1OIyuuCzKBZFz8FNsQqwinAqYgFTnW7dQ6n2gf8OIczLZ9p9t6dhuIE/uEVU2teGU7s+66YoxI6jk72DMrWOIYwks+jJUlJTMTuEXulU+BIHGZpZ0ffFjJbfEja1SyUj3x9GRFTBqfkfY0rfTnhlc1fNr8mGdFQNGkXc4zHlTUe5A57lNpiqppQnRpTIAIcjnhRYQqJo8xpLvqAJzKD1+BfCPQIsO6T3M3EanwQv6j6prP0YogmUJNTky0aPq9UTubkUQj2mWkkWbMqzVV5GDTLNr4xz5htYxDWSWSJbekN1dFGlX65BvYcnvSAIgnyIrELRJVG0r8Ez0QDClHpjW67j6KJEFVrIB7M1+DPBeo0Jztn1YCs7YiKYy7vw5Ke7XSR6B0KzMk/9wrnEn9uWgk2SdA84iAkaw4mVm53v+36QNOBPx8hbzTewT4Ksmbidu6Ln83tg+4zES27M2nfI2BvBLQbaWK/ht+fx5OMGXc23r1CtPIe/I6TBQH52RJTUlBCxiUImSVQ+twn0+CeOezCLCXf/4K6vuawh+xgqGBCpTstgdTS15weW/KmlXDF0nUS5l1CsWJW5RKc6w67Z8li4PbYDsExb7M9Cwxom3Y6ddBhCZp1BuzNARc4Ve3t4pgzwTJHRWfaTalk2L5LT2Y2hzqdWNWBVEfTVbo7rQJ5mpnh0CzLs6kk+em08PeZwPil+DsXg9ARp85nNk2YGNk8YQeYiTslSHwP9EyE6j9se2FgMbH2ZqtOZhbxHOVE+FDMImZakvgKMwwMmJjwGSQYrS9+RpaYiDKRERs/Q/q6BjXjfFys5fpOZTWPl+fIYGtBydSRX4aM3VTluR+nBi4PIEoyUzlR3ZQFFheJtKLmuDKFa5N2o9yRK1D9nWpixes2MG9788wHWfnOEtwWtYxLBAipAGUQR9meFlRqYMAUAm11XBWahaKdKjTrKj9CjZIizpLLINi4DVciu+ZQCTQctr66KeJwql99kKgOpzo064JGETOVXhY9Fu3em9byvphw+YYh1UVUtMfWFUUToDrOZiLp43HoMEViEOYAxE2qRUzI+jKTT+6XvrJq5N72aC+NK/n4oDKB+2sOPzv8G+cxhYh7C5dDkPJxff2GmBnstBLp1Neu3bzV0uVdr2UfBCtCU1OWgVOMZLNPJeS5Y57Cz7bYAAW70hfdnbA2Z+o4a1Y5OcKDyXKAPHDlWgPOgWaT5iB1oM50Z0EwfhZL3tFC/Px/h2YBqtZQCHQZTu0DNHvIqjV8wrbWl5s3zGj8OzvZwhQDdqwdWAPwGBjKZUIdEsL1mCcBlKy3iz6JM30AyFdjnvh7fM/9TZI17QfAh8Vhp8zPZtqufdnGpcQMpPO2zwDXo5h24gjf36jDnnodl2sT1jLCRB10EpXPms0QIWN+d55LQcc4l6uvAMdMmwToXbSv+6ZYBJQwoq5vhf6hoHbzIheRHpccdpibWJUX7wrzGhLlA4pQ443w7VFGavzMfkbpDVDtTP9Oac9zV20pazbcX+4p208pRzi1zRKePa9Xe30mQVsIdDImitAs6DwX2NIT97CBiSNMKotvfx1iCVaC8gz+awYfQ623NVl6hr+vO8djY2NPpd/aFxoi5CFWfx6WvurzojWgCaSefVzQITF7IYzF+xLIt5hexxnMde5j+/Lv8VrK9MYFTdL6y+11KiC+CvNCuNGk/czEaoODaxm4x1tjK3Uk42ezpZsMXHEexbl2GDBmzbJ0mmyHnJoEqjXE17A8J57Apzap55s4D+rhgaY2z6kXeFJtZ/UzIImkFyAzSw4US7JjaBY4dUMcdIZ/WdF1iaFZYjg1eyrKYAE9ggrNMvEUaLaHxPewv8Ba7b5oE5X0D/Z55DA7aygO9LGpxJPGGoP/JdnBCHB/SN4XXh1g2vaUeNxPbTS4PyTsXt3TiH3oi8fVITw85Ik1iqe139ukks7IfbHk31tfsiYDdq/tZR4FSnbfhB9/nWlizeH38zOchzxfbJ57RpKxPMtjM5rwzGBngu6omETN1RO00+gOgU4WgGh9kAJG3RXmtY5oCeadpxpXuO1UBm7dKdhCdwvZnqTYucOAopC0XRPjbNJMuxScm80biXH0iLySnSVncSKfwZTlBXOAZpMJf82cZfGq5lqFOtVIZg3kUKcsiNl8LGkHddgTM1HO9TXRfBebR2IJ3xs8zgTD6BL0kASSRTYb1bxjXyQN2NXC0HOzCNXMYPND0smYicVf6bUPflcmqG0Ps76kJ9tDP9g6HjzqaWPWvoRK2HwU/4TH5+NlICFXzaBp9EmZYjJo2AlgMIEEQK6B0NC4CL2ThwxKZjB6YLPSS8ZHDmoAACAASURBVNj2gDEY2WZwNDS8DvWCRj+XrlWYF2pIvmyr9Imo3Fi3xs7gXM/MDTBvVd+1ntMcujMHTbNzi+lhj6gwoMGDTnTJJmm0HWwS7Kuajx7uadoT5Ku9SjY0aHYM0KybK8wInGl6PeZ8dcgCdTqkiZZpOwlsK2aY5l8llEAj+xo7hWY5+Gj+V03fEH/KslbBsnMjNMvXxoNtGeh6hClZalJv5XxYOrMvIGnqjDFYVj1rRv6MtcNG86+AkSXug5/NmkBBAWYGRbh23D5pX504/rpo7LfsSf0qyb+ycbGWY+RMECzzGwZLb2E/ir/vRj37Ffz7QZE7Uj9PH8BrI9A7qKY3gAV9viZDttwyqObqMfSPVgAi0p3/c5g3Wj7F8Q8w7ynzCs7ZMEWWSm4QaJN/RYU5otaIBZCxcdjj/o2uMl3ZFBQjqmWTUyhCYMEocdgtA1eMoXu90BE8HGniRRO8fVKJDqaiBU5l5zAjRa3BTmMMejkiMhKJs5kMmlVTyqFZmhiSPVjWrGsNJgqmRXf03cRi84qJshNnGjJL507CeZQelog1S3rWGpjSQALBUgfJ/Qw2sQYzsXYOGU/qmMs6JIIHY55YU7JA2JpZ5n2lDSRmYl6LLZs/1tdeE/xl3e4NKBgXa0k2v/h+Hjf3ySYTz/XDnZqEsgHMIvzssHM8ZuQVmVSQbXuLynO0PmQGbzoq2sSi8VCgd02kFCDD/RhHHQ2KL3W84pbdWYS9CVbPNuoZXZ9rYq3DvFS5t7RD5Vxsvh+1RvzYI+S12h8580FleFOTTUGDgmWXvqi+ZLjHAlrFjJll4Hp2aoCYjTnVn+kwjE2fXbJmU9luqlmzNiVDzZq1uAkm1hoiWRWCBTcDu/qv7MPnfvs43mDSDgb/DhV9BjVFNKjdoWvN+h4O11oqCkyTfsYEnbD2NU012Q9JFz9BzSroQLUMfzaEbGJPjkSyn+hbegvELc5ZgW1BA4CiSbs6937VjOHwklAKP2C7vm22dkOTi3TX0iesBA1vutZhXqyBwITzhLKalu6N1MBtleimWNalzb/yin5RQkDc5grQNxm4UPZNkEZ/USLsdJ1xQnPUFE7Vp7ID7jAv2+H8PCbk64NiDLq3QVPFmepZWu7N0eTX3HYl05Wug9a4v1WYt5+gk/Zs2qS34JzlTO1HTR/hPi55XASwT6Lp8qZXc+eprUKzAwJxO+d28RguOoVmN4lh1px3jmAlhEvXTADw4CAwL2ut/JQ57EOHnWsA7uuyr309VKdcNBO/tzv510jT1ZSnHjGx5rxvUDKnyDzY54nngufHtczGnHzmUNEmAMjBTHHYR8oSwdc9PQaLG8ARNLkHE12Ts1ng+3mcJmK2dqQVLwCBFiqIm+7qXvm5ww5zE6vmHD4KzFt+hwpbUqz7enSPt1dJ3n6PVtvnEsLVbIQ5S6kaFKddGCqbnyPIhzuOwVcBqDWgKnxaIrL6bKxwZnlH4/Qp1mkChMNB+yh9mcMgz7DIvzxfbVINElrHnllL7lNN5M+YzYdHuAkrTAsFptb7PTrv2biTIdijpbf4yx8MMMgB5vUkUO93zEKfkl2QqaSywWjQtZU3kr5snWcgxNTA4iLYTEOWeWyqgxdHXgPuNQgMlTbmEHulyWKNhPw+/1lTnhaOyliKpK9c6zAvzY4iU2RHBH5Sxz2mjixVyIN5rVnP5IyFFnw/BzSb+jdNcYQI8zJ82wFxoK84c6z7PaWDiYehw45krcG1Bo/zmmHJkoFLibP6+k4zcDnb1vc0uHkhvsZBg4NMOve3CvN2GdLVXvP3+FkM2TJRsYP82h4mZp5DVptbtIkE54jYL+gtBca1RhJNA9MFEjvV+alBwbGNQLN5TAPAbi/aJm0NTn2QaWItIGkvIDCvCroeEj//sqeO+3yafROUcXWv7PKIgwINLM09M5h9tof7SbRAVpg3qeasfbGj/57LbsNPu9xgeulB3vPdPG/smwzmG7GWYQ1j5iU+fWGQMQEwWMKam9fs3gBchEiChDaPsiaCDArwofDvFArdOa1QrpUkPSTAnLVYLRPrPgFnrDQvq/ZoMK+FkOYmVtAaa1mVvmVWoEeS7FpjsLCDD5qCCmFrrFe44K951Qysj0VN/NMEu2xBNBHcpH5DD5qFOmbL1wHJO1IItlPnsGSnTjrJ3J5T0QBF87Azqk4N5XHCktEqUGcnWb5iqrD9csiaNTsMiGmCzrWJS63LjWGxIyXZ/ouqtdhhHxSaFaSO2ZPfi51cvqUbBHEuGoAZw30C2dGqwkW6vj8YzIvUTUjElMg/mSnYF+k3mt2bbaI7S9KU/LZkVUZ0JeipTcnI6SRbYMA07infs/hKtyXbw09iX7FvNviRCZlgHEt1TnrXZepSBtylnG2+RJAGuFw1BfpOSd/VSLMg6zGtQNnK24YXqoapJpbFSeba5E4wL1aYd8Y8gRsjK7Ywr2baGpybq/nglQYV+lU0KlOt+JEsBmDZnkWtW/kZ+f5+qgybrJ4Tt7PUFjTEN7QrnEoOzQ5dzaU6TJbROknJG9GakmaeQbJvPRApqIp555KBS4xGKeoE6huJtGOt4Rm4qNpOTI692eJiotmRdkk1yqSZtiDQLNp2W5b8bP8/2MHUdTUvSqDZTPmaIeOsAs/ngP0WRqJYO7gm5Z/cxyETSV/JU+45Y1ghY+lrqn0x4SjMq2kiHXpKPQBrs8OB8muHPEkyKwsp0nHxe7B2zFTF9YEgPxjzOOqORxoQGMjAAVPaWVY0WwEJfH1RNOtoGdZG2CVbe7TAodMKeEjANnMVugM/x2QO81b6LSXD5mbXisl1o4l1DPOaVbRQAdEFr1lYodS+9utxDN8L4nlWXn/KmSBme/qmnNE23EjmrGTHst6t2o6dZ83A5cWVtHPNmjVTir8mBGR98U/PQpV8ok5jFTxRGzOxdkZ0gt1npMsN51kJc3NcZWIIl1PDOZrMDnfqeMMSZDZ1SgYu94VKeEzgEjcZKXOek8KpGV7jSLo5wBemNfoN4cO9OuzMlDyGC4t+M5FqXwoN39/wsBjqAvnMYV4GEnqJ8FPHz/e+BOZNmDaIAgsLZEwgsRZ28o1ZMjv/rCmZke5tNcv33gYTm0vbDjqBwO0dHWA4FF8DxBxDsxzY/GKzzkEIwUQ6BkQwD1JlRkIIIiR4GzPHlnKgF68kSUYrLcwb6iJrOLuUPKWzYN6yX3tBV5y85tBZOPixZaqwP2POmfOAj9eUxSAB6z51nDFUyPac/Y0UiiNY4QDf6unQrI8pWbBFslOL46fBQp6UZBkC/pw4fqY6dxC1oAEUDVSzpGpKez+rz6vaxR4on1HQoo5vbgZJUcF729QxcWwUBYJU0e/ZM/xdhHgmg6utfZhlzaqEl/fAMj2zvkLWbunXn+LBPl9rZjSZH8JIXAUOZmr0PSW2cax0INpB96DIxzErGoIT7rUEHOYt6xhqBsf1cT8WscK98bNAfzMaXkn8XbxuhHnhKJJeBzIL9FE9RcJsRD9sRcWR5svEyChMExWYV+FcNdG8OuCUS2zBM3BF8k8ccDOHjv8bCTxzVDRezMB1J3vSwFXS2Ahg0CbykxUAB6z2somp5hOxZBdX80DAWqNHSQcRiWqL3El71nZ+dq+OvkCd+6kc+wQXHlsweHQwRvut7x0uufmZLfSf/Nx0LWaQQbPMKJtOoVmYIBXIuKtxCv7MoVmHee/32LF2OIJ5rS+ujsDmFXPOhcU2OJjofbGmeZdlBqcB8bUIGXdayIRzvBgWZsE9jiFtpUMuMiGZwZ1lGXu9rk2WbcGTzP1Y18Rz4rickOex8fqyBBvF5NVAolZ+qb6JRuNrrTRnjphFDo1Aj2ZXCa8sFTtY1SBNJL0wzm1h3iABMMCY5R5bY/dpCKozH1+GmuLUfJ+oXoN5RfOYI5ZpljlabFnPwHWYd17TVoUCE18ORQwmewZL6ilsY+FnOMzLP8mqHoJFth3mlThPkkM0mUHBdmjLgqNpQjYFX7vOEydLPuBExyDe2Fcgq/YhG8YsjXDUiiQK83IUHLFAs6Mti0THWcL3uitQ+jIYeDLfzh1lz29Tkyn0ZVAxo1hCLPb8QzkrUv1IeY+SGayzNIWs5mw7CHkeHdJGUkve1yQHzBhtG4KbPdk2SHnCna9rbghPV5WOsshn37GtzkftK99f9kGaSHoL85bQvuU9UamA6Auo0Z6J0Cvn+YEuYlhmqBuS9AHmkKPCuQXm7UrdWrLEO3XkO4V5tXq6omRuznRJqwBa5igUyZUqzMsaSnwT2xviRQg8BaXXdCZO3ciuaXjBLnsQOBcn9TVIbWVymJdNBnaIkXOQip9T88JK4Cwz2mRFQBPArz3Iu2em1P/GVR7vdZKxaxm4ms3LY5C95qTm2JRpujoozMtr81QvG6WAfSR+/sVAMr733O82DMpvtl36f1fTfk+1rx54r4kw33i9z5Ov3UWnez3Y6XntACPDvOxnPb1lwFmyedMru3yYwbwdpgEQHu7zuGu0rxBf0vniHZmHqWYyX3QFLpc12XQ1g2E3admgTA7zuvkmIQHw/VyiTRT1tJ2hcJRFHg/meXwwLy7DvCxnPVgWKyDOYV60/Ct+i1wUXJKCClo2VhglY+nXdrLJ3snJ9ipnTYGW5wxd0TJI5h9YPlWR9P7Gm95UZlf2LghMujFIcauqmrMixQ9xmNdNMTdjHOb1qdTnaPYsE4YMuePMXMpdRjFZNgkSS212/l3yg0nMi0HRKmRzzIpFsAZiO363z5IcyImCA+eAWdYsQ9b9BruDjEvhVId5TZhl1hqoZq5As6hOfjqMNPEGrkmJUnLVGOY9qGCRvtRUEiwXpfYW9zWpRuW+bCMhMMHyWEbQqDgzhW96yrYJJYHmZTFN83tNhmhxXxyPkkySXpFA0aoT8UYqsbFsTTxYW9Y3GTJaTSWqR0zY0QuowddCd2W7t9BqtS4eL8wbsnkxRqM5oxJwtpEKjdYEuiUs7WwzevvYYNkZ0FAtKic++WejnasR2xFMAwUYMDB0KRMqfk2wn1gyTZ45aq+REEtGqaBhPlnmd7EJI2aMm2jWXwtPSl+d7F0XZthNdZqd2ZgY2HQRmnPHPpNIXyYiRnHcl1NtRprNewDPPpZrb3vHWQPksFeAmZKTB5lw+R7PpWJL47VdnhjRY03kAiRpSgpxhjP7AsInnTI7j4uzdnmXouyeNOZgIICRK27ne7oSu9K+GNK9nmjSzRgSdBLBwwmdJiRkn43Pvc/XXhNOy5qMVmAjrq/Dz/KZV+4PMO9oVoTTXTyYJ4c6YYVWXg+Yt0bAsZznx4avbnIqg1OtYflNnR7cUoI3EkGmWJ1MK3aAbvYrDvtENekvbOoXW9eS8rgcjdmySP62LLV53AdEJjDJ5p00O7Zok71LwUlzkGo2rxVzdsjY0BWJF2jRBvLC0MIYPWWOY7ijyVKQzbI0aNwDDpTMBkcHDJjwZTurluHJHJUXUTtSejiCQMb7HVlkmu0f3s5KE5kWFHNNNKlCpbtDzqy+OW4gm6zY3EoZHowCPwtDXejWWGRAgYEE3vzkRSg4CMmihMECfo6cqgusaQQyRraSXzvkkU2uq5HGpy4EMk7dVphl3AJIhF2SJBHYzCJOn9+Zv8La7NI2WeWDQNZjZxnWUkdMQo1WSxhKXWJNmOwNxofqfw6xzm+gFS3wIYaNHcegpj1aEmeG87J5bw/zLvATNie9Ru6rRwW0xRkWnyuMVX6PNXADN7dwXJEcIQMYbB8HQj1Vpo5LzLlUxufWEqZa57ebdeXPdqSxwMwGYeszGsTDKwP1OK8dYLEcZPWRjp8hoLnB0OW9QpGJ0k72DL+/D9KuKweuUoFPvS//rMNSP8HuQc3XyFR8N9nwZO9MGo8QGk6G+nXqfNa+vKC2w7xQaQBKapr+S04WZP6obRxLiFiBGpwdeVCzw+dzF2kFzEqBirSGeaTitJ+bd7V0nSza4Nm84jwrMlEcbCgwL0Iic3CxOuagQltr45tTkyzKCTWbt1Qh8cVsizNYNi+fa0EBFiZzsK0IAkhw0Mc/hMNpWDrygqg2sVyqjqQ9d5An0ya92fR7qwsF5ottLAt1yqTmhRdtMEeTtQtLQa4AIftPEpjTCsBmx24qW7vBA5D8YizRS21eL44AAg2XjGFxzJNCxle2Icn3vIsDzOYIILDk9qINDv/2PcoWY90yS5mfwakeQyffnyhhdv9sY6eJ7BNmdrR5Lvh9n7noNtJXl9LnrvOetQ7P270N9pwVwBD3Q+7LAqad+iDJ553NNdvjQ5c99qKmJ0pX+zx5wQpPn+cMMKkLzMjaKPtMrBKN3j/OQgI1Ws1md4IaRnC6GzOWbbnOMM6Ij57NG768BPN6O5WajjjjXt+Y3xp6LdSMrRnYHJtGtViD2J+57DJD8D0XbmL5m1LY957zPCo02keedepqwtAwynmenarZtpr+GmvY6g5G/WqEjCUrgCR+pz6M3eP70D2bdyQ90QnNIGYCdn+lToZGybmzg/lkaOd72OH/4gjZ/mz1nzguQLolgM3DGC/zHX+joe9o+0om+5sMPk4aEwCDdwXoFeJPVRPEvnyuuthXrhvgXNuW+ZLpsxM/MZU1iYUs7AChAus6ACTvyLScnbw81wqNJmn20+fRy0Mt1nVeSKeK10mY11XemCtROScKCkGVSzvUEGsqjjrO2s3JjosGKWTgjlwDV9KVMB51pqkmdq/BvKKfDhNLQMi1Nq8yO5/9wvk/yc7LcB+A81ql+l9S4tr0ahGkThecn6+QsfhLCvMiiJOriBqJ3a536Q45PhRm9MxgSfoD0QwHyZdSJM5NkCy76tTWJ6olgCQjmLfdSkEF0SaMGIsGenCAcUROncFSAI9zOqYDSSAx2dLKzr2sG0o4xYSpjQED9ht4QvseBbJFAQy0anzPS9mhaDn+53LEoVnoML22y+O9IfUPDzQ+NWDP477XYffagcakwVYpRicZuJxHZhrTaYiziMHMv535bKyxLzYa42Va4twztEIbmmaiwd+dnFtSmcDNa7Zm3NfI5scSeRjBkklJrRln3sk3txnMm+pO8cokj1K0QUwBq4ulgRayOfQCbxaING1SmYJKO1RbHSCUf9FMGismZjAS19Y0dcoEBpahK1KFE3Wo1sUSk33SIwtKAKizkpmWrEu2H0Mc3c62LDtWTpY8KAfdJKQI84KlPyQlJukrqWQT2Jk3EjFpZucAcyY1DV3R0rj/QXwUKwAxhsIFXvyamcQCjSyQygE4yVLkRWOMKgc9xWNkZj2IaSImCzv5YpZaZUYtgarw86ZTk22kaq4lN4v0fMU8WptsPOtktkWY7DjhMFRsZMe6G7BnhI6pUStfamo9KCw8SRXHpGn08mw1jXItLq4xL4XLLSjsAtfgfQoaA0xLKIhyRCuFhpzu3Hx3EyuvJJncCea1gDS1JpbRxxF81rY755d2j8IH7tWCYKpJ3TlGRbtYmjNuWA6XFCnOz7c4yZyhSVAw1yjB2dN07FqMzitmOKTIkqs8Ay2VnX0a/pftFCdXwwerAu/JkGB9xXZ7edt6W+v8ikZRQEDGIGVNyYilc4NDqrILc+wr1FkYhDXjIbNVp9aCaW82wbTO7ySVUhJPtkbPxdST/fPyjkm2wEpf+0xS0GFWowsUmtV6wiB7V3xerGavfF63xYpm54ru7IdNmapRTwqxC8zr704L84UGfNg7irCbLILvaXye+e1B5kLYgmTV8MIi3ZXAeiWKSNdxfZeu9dq8lgYRaFA66bDucLAyOMWUAtMS3q57ucF0hBL4FDg1HJtmNqs4+ZJtKubXJM5/7pAFN8pmmGRVO6xoQ1HB7mSLw16qAyr+brlcpGaRZQabhGKIVkr2dzU5zp18NuNG8yM0qGXy36spdsiwqRefFikozqRKVHnTISkwwMSyUyc/CWBgzilrpuu504q6dVWqghB14AfRCPrUmT/hRxZkqzMl891RZnPI35E1kxaAQDHvODbJDMbv7QUVGH61AhBCOOyAg2VrPxhp5PHz2C83qRM/JKEUZ+AjFbhdNoVxoQneRDbS6DBvDkAGK5Kd5l+lg201lunvdK18Hg0xk5PpdDuCzqHWHWBG0WjilO0kAIiAEBWTv1QE1aAiOvPkYGLF/fOuFJautaINc34JFdjd0UkhO3V2b2DGmotVk3oXn1ezaf3kVzd9ZvekCGNahYuy59gkV/udmjFcs3Yd+osBUH9+aqDSWLHPP0g4n7eoTSzpP+SAFQ1Z/o5QeLjHs1Yd/CzILjqEadlnqcnaDTBxfF8wzeR9lv3ZsnZZPWPfmFZ8TvPYHR5HM3G9tkUXUjVsD09JS8JaQ02j4Gk+Pz6PCTxoOJ8v9yPjWkX6iOGD8lGkowjLNzTWkuq5uO+RBkEs1b7IIDKtnAGSSWq8okDHqtYwGkhuLpGdlgQ1HdzNK7cXO5MEGnVXrcH39uZn9BZk0sNstM6S5QeKzeFJcEwEQ3GAcXbU2YLDLprLNUDnDrtNH5t5JTM4aS0rdzT9GfwzaibWPlotRU0JO0ZBrhZ+drTGn+HP9/bBgQQzSw56Op2skWsmBtpYAzmUfWGVEVlDcjv34fV0BRo3c0n9IDUV3W9gf0I0kNUZ5vQUmUVz2HmcPI7twDX5gHfwchBRTLVJi/yl+xtli4eHLLXIzHTiPSCae9ZBcuid58tP0uU1iZo/4RzGF4sB6j4i1iYOCBlYRr6T0LWGA0UuZQsD6QY+Bn9USJpDtuShHGmQ5CV0fDMBxvz/2oNtoIq48qwdggaBBVvvSMqaOshUsy3dJ/BcGyiSnEodWDJmQ1MjM7uzBooAoGSnlm2avo8gZz+vZF6wrPQFamLFgNVkRRDMNBQndBD73hzgCj9jCz97PMfndbJnlIJ4JllH82liX46oZajwt0cB9R6FpT1uIBYhF8TLmkzt2bMYfBsBE7QGWU5B0zPhS1EMDkJqhNA2uCmQwAwVC2PItn5+9kHWJ0eNNlm02ivZeKXOqRblcNqghMWmNyS/7hQEqHNBRXHSnO4a/bBk6XSd5p+hJb+Kyu6OWeRYg3hUVE9PSjv177Wc3eROK5a8JTe1vDYuFEcdg83nh6CgVMdrtQlqZjDDvFK2UiWtzgBrE8yqTToVCmXL7JRriZhychUy9IpF03jaSt+pT8HbVPSIZI0IuzZxP6hL1fdiKVzq/Cr8rCaAPj+DaSCGQmXvPO/B2HP+kYMC6NF3dPjZF7lv+uoC/AwFfpZxZU1Px1Jfis94G22rsKE6yYOpohlNm/Fed6tmL9pEd26qz2RJo4mxEIOf5bmenMn75vd6wI5oIC4ywRPNAccH15mdfmlnDcVpPjmrZroaFeYlRZ1LNq9rWQ2yuiml2tcFjpdmLTD+VGNMhoBJdW4Bb8hO4epADiryILVrjWj2hpCKJDJ2VuLJbOwSvztmowUGSYZpJ+MSwfpHwGGQgUzT5Dbh3I42Qi2OeQpp9yH45kwh3w87/ypR8lnek9i3AuF1up1C2v37U671fzsvYhZfqtOh6SRqpjNLtl632IoZnPU4NelSs4LtiIcGuYtm0exYBovws0EziU/r8KTONxN4Nm1Vx6Un0E2G8ZcCzF1hylm7ZbTKztFsR5f5qzKDSWzJoGwbFxdU4BSRNHayiSxzXWIdr5mRPXZ66hN5wBCNwRh6ZqK3WAIAm2sop/NC4jyyXjenidk5qKPdeZTboPdUyr6a1kCzFrgPLzN6CIfm+LunWgGxwPjuD05aZVFpCaqgQPDDkJSeHBDyAhZutWhQdH4gmvlKkg3OUjZh7bfhh/kltj3v5urUJucMNct5VhWbPDZPiMHI8qAnhAqI9tNiNJiLWVP4BrP/TCHnhvxYERCY18/Rs3bRGqXdMzcnKwjlWcYmb4QY/R5LZ/HD/KVdkRKq7RLP0EJ42aLUNVKtRJX11Cv0dkZoNMs3l/q0/n3/Bw1gYFpGESooBblFu3m7+5LJMgyymjDUGhE6ZjVv5Ihm1JiLj1c1lz5eT+tSM9CQNkX0NOAmZlbW+I3MV7L1Hg0SHi1BETSdRfqyI+6yz2Eys9njU5NVcDF/yserqeowb/f38XesMGqhL/LCH9U8NyAkmM2BEYr/kUwQoqJx2PW6jbofUEyuLp1hYg0bTJuM6XCgdNgTHXrMQ2+OsXKaiKwMDsHp1alFgbYvjCeKY2q8cSk5KsG3ldNJ+TgzU8GTpVhY+kXeINneNWIJxRYFH/fFKlpK7fcE3Zi1ndSeLPk5o4T83X+CfKH7I3jVO44J8DO5r/sX2A+dqJCOU7l9h5xU3qi78Kz2m3LhdmOBtqQHusiGJXayB6nLK8UeLMsY9HPACj9Tifp7VB7U75hGzUFS518lPVdglyMZmIS01I+YiSKgD1oM22JHhJdbfwbyYTp5OyTcjZkut1ore+hRyvbwTLBfwe9nzrFsfzUoW4Sf1jjWjR+7McsWYpY99y/Eyceh1625TIsGVnB2tfbF6e3o8S6poaUQ92i1rKxQ3YUVgBg7PZEYrAh13ysBO+SNfj5lVw8aNc0n9MXRvw3asRe6JWYOFNVkT0LXGIPuf+HSTNsNpV6r3vPeFg9k3sAgHUnB43GjsYeRLe2tSz5kdSfRqNH2QUnQ7SDpGK6N2B5VCa91qmqN11yTNEEPtXcntXMIkuexrxg1Q2dClOWndzDp32ZvFnQ2tMk9g3/Q6z08+VOmtB1SchhymzU5yMybgqIyEZnZxH1Bb6NnIuEwudjM/tOtzlrCxo8bczGmPEsaL+l7M9WYYQM06ucmmo2sElmqHaZybgpaRQc9O7FkNpXx8gMHiRhigVqp1xgK6s/kyaHbodQ8EGvBg4Mb2aWIIpT47XqtTSb2Gy+j7hQVSdYJqsT1vWT3gHrUvgGNdAMb6PkfdrycEeJg2tbn1+tzQRNq4Pd3AcgJl0YrLLNSiKX5KRSYQ5oUL7a2AgAACgNJREFUv5NpaRF+Uve4T2kzkNACM8vmAtN2y7RxbFG1DPKpb/jA9vn/9Mn9JyfizTBAlxfU4U6pJh0IDockurY364PVIe9Si0hW6mu/WbWGaBNvVzscXO2L1ugNtrTDeso9G8vANWnLZ5ZLO2sGp309OLLGe8wPACtHmiU4l7XQgquWKWeZeH7HjR6BJpKfNZCvUlLb3fqyI8vMVr7vW3l79IRBgTNly6rJgHF2nneNd7CLy1uuk9XdvNimAnCID2BVArfmA6DBvm7abETimQMMVZvxPGwNsrXnl+PULgbO2lELWPPLtJ2zlX3r85S1dE6ynLqnL3Br8969tuMApN5zbwOiZbbal2fZou6kLH1ZDStFKLaDoqlMKlJzK0lBO7jXVUje9t7I/G6xxoGmanKJAu5SpQmnIzMFC4ET1V2ww6CAjJzv2BH0PSFbAxzsvLzkA5MobTcp/c73bz4PAH55lUG6F/Z/+qth+3ee23Zf/+8+cfXznKXAK5gSwfVOI51DR7ZzT8chgLBFjSUvJinO7EE2ruRkUqVgcGY7on8vongGG3ax3R32wRgqZ8+5qikrrk4F0eiUGCdNL0UzXwTNYt0uxMZFq3lBDdt19ZpGoK5USSf5jv0OvMZCWFb23+MVHaf6d2JuadVHu7+bwNqrdGPrm000xYeQVSf6pEhy5SDAFi+ksBODI+K9U6p7P8QUNMh11M1iElewsTss3pPmP02WtsKSU7TrpOYEWyUab1EG1TiE7JWR7yGXiSRFie5pPT5GE4VQ2bnWDGNJP0/kQIhJJzWRVLfxuHozW6WiZKfzNU22nSJZVZJU5lG33XYOwOh8SUknqLTiRXQoh/POTYNRKOHk5fqldFOHzKyiLS42zBzQbYfU/c73bd73u5+7SOm56VsiT+D+o+9+AQDeVVompMNHL//8w13+yz/6iatf+PmXx88xc+xHmHY7dbj4xdgByFOtRBKjpRG5adsxnAvviAcEyFhLhYZ74HR7he8sM9iyTzwR0A+G0XhCTRAMJaDkHrQsTK+55YTobVpDS0GKnI/7qu+o7VSKiGmBpzGXGIxXpUQ9TIMJ0w58yxLk7FIxVk1roJhkaLSPvifEEZAEzTuKpSJSukjUSdJJtF2OizPhMk6eYq+9uc80TZqowMxzGHm/fJXOch687KytffHI+HvVOKrP13w7yUP0cZX5Gqcwj1Dn3nYHlPX1oIfvWXc6SlCTrCwxtaAbiGWPhvg3qKfvps1GmWQzQLq4wO53ff72/d/wgYuhf2761u7Ldg8Cf7zKDMLdsGp5XwQNxp+6/JrxVfxH/+Ol3av/5ZPXn+YCylLe86B7oEbG6KeSyE8Y0h/sDdG4QDPMPE++bQ+/R+axiH5pB2dEI1CAuBTz3730qMMbfg+G8yW8Gkp93rwdTCPGvvyZsd3vCWMv6Sr1gE09BdZrC2lAzQhEM17JNksLFymSqBTbczQ9a2Gezg6wUUMbJVYyWT2wUjDDzctsy2JaTvwhZ4pRNGM5R6TzM+ZN07BTzJ95uwdFPY4Bfqy2MVJnBs801eJvo5WHTZaB3PdYvuMa08flcxfXxNfRhVSklcgsTlN8e6RB8gCmSlU5q0RDGIDMGAJG9Zi+/n3D533j519u+/dO39p9+e61yBwA8IkSjDi8+OxTAPBF0eyafmnz7vzp/u994rXDb/vRX77++KtXYj5mnmBT2+WAGSmcTyVkji5AsywlFIQhVRtVkSv7jFEEIb5J7+Ggof/EAjXO20udqEmfAYZYuLOlaFu9p++qEholOEdp0iOJq73bFIRwotKMUiz39H2VqOPY9GVEyhpCttyXc+vQik7I/Ilc1WIOiFr8ReHopMVexByQQtgWatSYiB2RbO84WdGJpGeg5OJo4nxcPF6s4yV2XrNuquIAJzqjc6UZcWxHlbrQ3LPWzn2hHJqTbB7zrC9+DxdYce6jYxzb2/VtacWYQNbX3zcRlb7YnXJtItUX3UkXxxzT9gLSVz07vPf3fuDy0pjjlbDszCi/NHzw5TzbwXd48dnBmOR+4cSHCcf/tf1rrzykb/nU9fhKtiQ3EXXmb0QbsCjsNP/dP1v7Pd5Tj7+pf8d2CP6OX0X1Nfek5FYOHfflWmMyyeV9YaM1XJt0QTOd6Cu2u5izvJeicVmg/Ngv7n711TE/5P0cZFXdU6eo1FNDuvj9L2yfV6a298hq4onTlNbH5RrT2296xzh3buMokFt9I3R0w1/F20NnVIvZl+RLe0gxe9bGleM8Es3Wt6wjBOshzekp0lGhiZY+UFE92c5LkL706Q3175v+bPclu0+H2wpzAMB8iysok3BfHwCA52L7+L+3fwAO+AI8uR7LRXv8is++lr/xRz724Od/4yo/9GVgKffMRXfvz3zp/S9971P4H3BDH3sy46/Phc/mH+u+aP8LofMZc8ASg/z971Z//Ts/1D8NAF9op589uR73xRDzj1/+jV9/Nf+Jf/Pxh//31Wu6YrP06cvu8k+9cO+3Pfsu/Bf9111935N5f8Muds4/HpkDTjEIa6fv+FDPVS0u335z8Za4ngGCd48/fvk9L72a/9SPfvLBLzHq80efv//F734Gf6j/2qt/CAAv2cI9uV7/69Xv/8iYv+v7Xp09aHFHoZtuH/7IuM965qReNR6n0Kx/F+eVULS2aP1pWZO1fIbj0wF5Kv03ta0otkN9fmyHBsUqDkyzQ4uwjiueNP9m9PUdH+pf4VSY/uuuvve9P3E5/bEvvP8t7H488wz+k/5rr/4xAHz2w/9s/FXIK3355XsdEnoef4V/w0RGpG2G5k1zAdl5YDRXv4FC8BUsMBvhVEfOJvO/wPyBo74cmg0TmQNki2G92sLUi+8e27MU2ZiRXnlGoNNM4bNyvPjx8/xa3nKLlRAtXHveZ3FE4WdhjMZhLy+LcyaKDrDfQxZ1RgztPjlQmQ58N5kzZKpjwPC9Ag3jfLPMnfqKqRGn+grP/vAPjfQdf67/lKRlfN3V337Pj19OkOj/9V9z9YMA8JkP/9D4a+UdMTDYQl8KlihC1GMluMlXvWwYckjVAjLWR3HyM9mxAZ5GZCnGeX6KsTMFFSidyjqVA5YSFaZ0+GnmwId5K+0uDFohScEBx/m7R6HrhN/mi9TwehDoEJhlhTlgjUEiV6XAEDMRGrUGVe5d1SYFlqqTsHj5gjfaBFOYKAxjoGXtFOakPj824rE08j7jYsz6omZ142ftM2JfuHBPUiaBBJ/6jm/vof+6q79rn/zqh39o/GyZtzjevDx3MwEUqLAVQH4sRNFyYTxoWrEIpxiJDhKWmunPYWzYUGYxDKLWCMwe41elw7CWiM3D2svpLlozNLduMsxp2DNs24Oe1rTIkQ+ydh1efPas7z257nw9b8eev/RkCo+v4YMvn/W9R6XT2XMA4P8Dqh7Nd4KtKt8AAAAASUVORK5CYII=';var iconRQ ='image://data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAEUAAAB8CAYAAAA/+H1MAAAVXElEQVR4nNWdC7BV1XnHf/ucc99wgYuAgKACwXLFRhHBgIJoEV/xCqYajGPVmWZibZwmjSmdRmObmFprq6PjOJ0kbWNMHE0jQkTxARZ5GMQXPq6AcEEeIu/L5XIf57F3Z6+99j5rP845e+9zDtjvzuLsx3r+17e+9a1vfWujoZDxpHpXkNQ0WqgUJ48MtXlhaqHdAqkIIKi/WoHnQemqTd7GGgG/RoHngVQKFC0gJGTQlF8vUCeLDE/Qyf/qRQByUTFQ1IbaQCQDgheYE8klNqmNNBQgcgHBBsib1qEwoNgNT8lQI4N9n/Rwz8kklStMALIyZGSw7zX5PhIoduPsxtpA1AJ1MtQq4KjAnEzyAmICkQb6ZUjLtmUkGDl57wKmGCgJhUNqJBANSqiXwNQqwJws2aIOGxuQtAx9QK9SP298PSwoKEMnJRtuAtEEDADOAa4ATsUtV74MpMqTL4DlwIcKF6tDTA+qbxAoqnBNerjEBORG4LtfgqESltqAx4BnCghf3TuECjVMK8ApZwF//f8IEGRdzTpPlG0IGu4uKjZ8VJliC9g5MjOT2oHfF1GCig2nUNplmWSWfz3QKut8KbBVAaXgxFBK0CY9gvZUJc5rwP8WAMGr/XoBCVKeqgHUIAmKSSNkG7wzZihO8SptKjBJJZ7hSaNeJwLyUtPoyr0dvHEqQWpeqQKAaF6ZEkZ5U4EJYjcVEK/6H9QThnxueFRvXcmvGlyTKACIj8KsfVQVv5iATXjiJwJ0F68+oSnXSQWkanBNIqz2XUymeNcyQZl433vXRwkGnzMQjAR6xqBrc4/S8KQyLeKRM9XimqA2RZp9vBkVQjZowWiti6Y/MZOJ37nLidn50TpWL/w1nR91STBUrrI5p5pcE0rjroS+oSKfXzgOmtTMuFtuccUcPHkGV67/F6Y+PENZIngXlykPWKW4teJUKVC8wybFRU/dTKpxsC92qrGZSX9zJ9e238XQ809RFpfeBWah8V91YMoFJUimJDj7h620TJlVNOWgSVOZt/Z+pj1+saI/FAPmhHFNpTglD0jd0HomL7otVKWTdQM466/+krbN32P4zBEKKCeVa8oBJchUqTHr2TZqh4yKlFPzxK8yd+VP+dov53wZuKZSC7s8t5wy7eJ4NaltZMLttzF/292ceukoD9fUeoRxVbmmUjKl1LPwNGDc2Vy2/CfM/PXlaMl6xepX49OBqsQ15YLiXdAZdDz1LNnjR8urVU09426+mfkdixh95WkKt5wQrqm0XcRg/R3reOG8eziwbiUYgZat0NQ09izmLP0Js565ikSNahcOK2tiUSVByavpw2e20LPnAG9++5/p/WJ7WblqqVpOv+GbzN/+I8YuGOvRabzgVGT4hFHzi1bZ92Ts/OFMf+JvSdYPZNiMbbx1538ypu0sTr9xPsm6ptglNY4ez6xn/pHdy5aw5qaXyPb0BYBgBJkXo1LlzYoT7/gayfoBSkPuJdVUy/IZ93D4vXVlrWG0VA1j2r7Bddvu4cxvnVlEjymLYyq59kE0+LXLF/PO3T+j/9DnTkPGXn8Dc5beyQf/9BJvf/9B+g/uKavEhlPPYOaT93HZ8uupaa6rtFwpV3nz3lvP2h/azOLx97H7hcUY2Yx4ZnLN7N/dy/CLxrF4wk/Z+ftn0TP98UtPpBg1bwHzO+5n4h3jPfs6QfULTZXQU/LhksXzmPLgFEbMaiFzNMvrX3+R19t+TPeOdiu2yTUL/py2T35Ax1Mf8uqcH3H0k7fLqkHd0LFMf/x+5q25ifrhtZUQtuWC4mbZkXPbOPvuH3D5qkeY/dwVIsaeFw+w+MyH2fz4L8j2dIlnDSMtrpn0/Wksm/JzNt77CJmj++NXQ0vSMGIUzRMby2yP06jYNfFcu/NKpJKu+22/2sSOpxdzaMNqMAyHa+Z3/JDOjw+J4bbnpaXOcAtL2Z4jbHrs33j+Kw+xf02nZ7cgFqWMReUkd62QNTAUoAw3C7d+73zOWLiQ3r0dYlodduEF1J0yWnCNOUPtWrqEVQuWceqlf+SCRxcycPw5Jco2OPTOKtbc9Bu6thwN2BM+aVOyOn6L5zX84qnit2HkOE675joOv7+R3UufE5xhcc03mN/xdyTrkzw/4VHa//0Jst2HA/NKd+7j3UX/yotTf0nXlmO4/U6K+p6EoXKVNwoKtiHnTWbuSmuMa5pG4+gJzrtcXzfv/3gFB9Z1MvqKDUx7/FsMHDdZADbr2XvZtWQpq296lfaH27noyWsYMfvP0BJJDF1n36pXeOObS+jb3+MBww+Av1YaBgkRNDR0GXrR2I1Gq5VHpTRaPzBNYyaK4CeDTx75OQfWHRRv9izfy+LxDzHtsQuZcNtCUk2DGLvgeuZ3TGH9nb/ilUsXM+rKtbR8dShHN3Wy8/k9NE+spWc/ytC15JeuXJvlpKhRzN5JsjSg00iOfrJk6SdJH3X0CtcNnXY0YxHZymi0huiBcNPg/jXLeffv3/U41mR567treeH8RRx863UhiBtHnckl//MPzFlyJYfe7uTDB9rZt3ofV715I+NvGYdBDgMdQ/whetxwApIj/JOBIblFJymC4bMv95XHKYZTmJ+ObfuYzg83g2aIoCUMjFyGNbe+jCHAUHOxGtO5uZsXpv8Xk+5aw7n33krd0DGMubaNBVtn8tniFxlzzWXUDBzMy5c/JQBRZ5r84NFkQw3fDGkPHRsQC5Sk0o6s9gBpPyhdaDSgiVGXkBlpcgyqhdgFIN74h0/nx5tZOX+Za1vUcPmEWM8N1xC0NsnaH93Kll/cx+ynr+C0q9qoaT6FCX9hbZcc3LCC9LGMZ54xlDw0p5GGR/hbdU4qv1bIpxV6VMqtngPDRBMT1JIg6QIjUYAnErJSHkGn5RnbAkR1mFEBCfZAyPQYvNb2B0bPW8+0h8w1TjPpzsO8et1vnfIMh0sSrnzcQPs5xVCGju7I1Rytwg3MeZBHtJckKRLiD/lrX2sBhaiFu2ARoKiABG2mG0par/uVle+ul/ez6+UnlHeGwhu2LNOVTXs7plehtGWKm1MQv2a6Y3bElJJRQuKVICtgSIp/NWWYeFihuBaggKI6+RbSN/P9694mNQL3lfOdYDh113ygGK7hrimApOR1Sg5pU9gfV0FB2b+1AMiSFJOZ7pInluTWChTqVMjI0f3Zx+x5pd0DikW6q+Fqas2VvxsczSM38hDmhWTQ4HZzSpBMMTFIcpQ/8fun2CybklI5QY6k+EuIcWcPIffwsUGz8+h4+mk2/Uc7B9/pkkW4tUsjsBHuxujKO/Vfd68nPTOP5oBXzHygyhQbENOtdLAlYL2gIFmo1pmyDAmG4SAc3BvqVLj62+s8PemVGbqvp1VwvM/8s4davvcdPqC98W2dRAUmxWGGuV1HvVNyPwb1klMsqeLmBncF/SyfByjfKEPp2YQPSPevCk4wJ/nfeeWM+s4Par7TLQE7jEPeyrtBaSXLVrLoAhhrGOmOtuIVkZojgHVZuBcePdC8oLJ8MDDF3vkb751hUIDNv3P7V1ucUsMRmvwOxn7lbRDH6WYgOWfBhGR8w8X06pTsnh7dwtc7beN6G7bx/pkveIgUG362TLM53GCI8Mj2kR+UYeTopQeDBgFMUq4wNGetYhdRo2iDYXveW/nyG18MFHf7cujiz+LgFAdocg4uhPDNH84x9tMiEueERLGuDPYpKb+ORkvJxqpkNSBDjq300x7YkKBFXD2TSTLBl19x7jPreIECyUGXGjmEzwtZ6YJBqcegjsOkGeAsoTSypFlDg/B1rxfZJrkmMH0psny4u0jzG/p4vyBHNHIJtdwQqww39dHLO+TEn8nfX9AkVPrAbd0g04GF3gi6gR65WskJ+0Oa/fTzhHheLmk0U8cd1DPdpVDZS/g6WisCiEEfPfyWNIdFO0xuGcBnvoWpQoVMB1bEAeyjm8FiPjLkgaJeNpBhO3VMQ2NIgX3c4OnUemKurCbLtKaLzu3kOEo/2534CeqoZ6GTRmc3OtudmvnztfUhdW1kAnCUXj4gQyc5MWxNIPYykGOuhamHioMyhD6Oc5Aso6VRJy2ly0EyrEATi4GUCMGHoDS5kEzKOLVoYv29kXpuRGOYiNXAjfTzkFN6k5BXQ2VNeuhjGTq9omOskFNW4KpGa6+dcxIUq84WIFlx38xmqagGcgklzJGW9nkKX7CXYXLxlBWgWOpczgFEk5qi5pILtu5iv0tJQOqFuOtjCQ3cIoEaJeTHcVbTwDmkyHtDpVlJjuMihS46JSPqkQfFvTA1nD/dAUYX9dYFlwzhCMEHLEuCYrOjqcZlSLGLNBNFxkkBRlqCkhVcgKP1FucUa/2tSwvMQdK8Ti3zRMw6riXNDhqUYZPlI/rZQo4eAUqOtOyYrGJTwVWe4azEbWB0569RzHhZBRSicoodWWcM+9nKSHIMFsgnHA3BMhxpDme4tUjNASUhhlpCsYpaqTeSopUEY0T8JuZLnxPzfSc9rCQrhH2fMDbrIli9briGTr7E/CBSuca828coDnhkSaDxIwwoSN1wKxmmKn1hbxAkHa7yc4km/5LiLimbkpQzjfnbw6sM4FZp0BrjdEQPy8jQLcCwQlrKhaxisDZc3KneG8rQMkSXfCi5RAUjMigoGWiMo4tN7EVndGDf4KmgfW9xSU7CpomNBktY9ksNaDd1bKSG85w8+1lLLztcYFgh53BJHgA8wyjIXruP8ewpBUZYUFRwzEZ9CoyS+kQQV+ABJg9dwsXUOSks04I/ulhBC61o1JFjJ12skjNGRnCGrXTlpLj0mxlUAIK8JTcWEqpBFG3fp1VMZVs9HkT567yZL6mY+5KOoViXK6icXInYKmE/R+hjjZh+j/AcGbFZlZZKoy4BwVny6678Ux6jkfskCRyhVShroSnOvo9ZgOkkYx9G8HOM/x7HaKwrO3iGmImyog8P8waNbKeX/fKNLuGwN7q8HRhURlD570VtYHRQzP3Wdj6QpzfDgGGztt2ohGN/yU+qulibZ/hUmRfcgOgyrd/0WKwOpmvGluqDYgFzgHZ2A2eGAEbVIfLTti6VPYP8RicSKtUobjg22aQjTsNxpxk22Jvm1QfFovckKKmQlcQRgrYdz56ucdnsEoo5SyswqxQrx743jdEfxWlYfFBa6aFdFDotZCXtRua3WfPguA3jhiut4aTLU5iy3qLVOZ94gkCxyFSIzpZCN84wQg6h4LhB4ITjSnNj6524jSoPFLMn2lknP7JAyAr7OQdfoEh+YfJ+U6oPsah8T6ZWttPOTjlNx2lA3PtCafsEKGVQJdy7kN88mFBE6J5IcF6nVQATmyoDSiuHaRdj+KIKNzDqfdrzUYpY5Aalvay8VgNT5JcoTtRQ8d6vArpLtUN7oPj7Sg0fZC+9Co6R6ETKEU2aBV6pREMqCQpyNTqzgNAtZ6iEibtOLP4qQJU/LgfPK8f7vd+E816Xui8WN6UEUyt+oVKNqDSnmGQac9YDs+V9nN6P+m6t/FJXRagaoJj0B2A6MLDKYNi/SypZ+cofl7PI3F1cGmMolHqXCrg3F6Y7Kln5anEKUl+YC5wesveJGe93la54tTgFaRN90tO7xXq/ECcUuzZX6ZsqXfFqcopJn8h1yOwIXFLo2itHzN+nq1HpaoOC5JaZ8mt8xBgiha5NwN+tRoWrOXxsOiTHfdAQKSc8FbdCxoPF358ITjHpOeBq4DSl921PBNVjwe2jZu8RuQ85mfE6gDXVquyJAiVDgv/G4EGxla45HGOTFnCtuf61tkGt80Eaz8qt26pQdUFpEfl/RX6d1PSkM72JxiuN1jwpvOBY9/mdP9Mfpo9BjEDjOhC+Jp9y2HV+qGyqDigt4qsVfyo/ZlnvPG9gBd2MV460BTU+CKj8s1relN4Ow2W4gBZhLPhAeOl96UBpEZWfBEx1gZEv7Qg1bCDNjJKNzz/LX2sco0E4DqpUL+04rbTwtpiVDpc3tCo3+7SIrxpfLa1vfkBsamANmnAk9H5FUPVv8X7pwrquYZ3cjQ6ieln21bIusakyoLQwUn4Qt/RXuxKkqRPGqISn4YkAcPLPTFnSQJjvIowSdWkRM10sKh+UFmGwvlp+iiwcNfARCbED4G+8/9qKk+JNAWg4qhMfJm8JdEguSeWB0sI4+YnnqPmYTu4vekDRPFyjhgyNkbctEqJuVh0jJ4xHLcLdc06AcAxHtewlJYZDYe6wn9ewnoR16DEiaRKYYdUHxZpy53qm1uiwNPGZ1GoHyDBQhgHCCd0SnuaR4HI2t5KirladQ1HcKfkCWfE4ZKabIfQY86BvA2l6UL97ok7Npju6efj+dqGHWMbp7phlTgu7NIjOKS1iM701RMwgOhf4jtRjrJ6ro5uk2PcN0lPMc2rHZNypMu15YQoKoEmy7iUpzvA5N4Yc0aTn01UOGCo1Co8jP9XSI9y/8mSmvdLjRRWlDueGiRgNlBaxkIsszaWR6cKCb1P0CwDcthZNckkQXajsFkSh8WFkS1ROGRtDDo2RMqQ4NdDp8rKvoUcOq0I0Q9YnCiXDpIkKyoiI8Qndo6avfx1djvdbvfuscAEq/nXkYBpeuirRaGjE+M2RetMEwpQhNfSRCqW9jpVlRKGSbYg6FBpCxFFpZKTY5vBp5Ig0DYSlUfYnPirVhqigRI0f/btrtZE116gdVbINqVK+GjZJY29UC1f5Zw1LU1QQS7YhqkyJWoG9EePHoc8jpinZhqig+L4LUILMsb4zYpootDOiPAnVhqig7AsRx0tvxEhTzbxLfqMyKig7Y8iVnXIhV2laF4MLc2HSRAUlIzeiopLpoPfHCoKyXuYZlbZJ37yiFGdB+H6p42YBZMZfCbwUplJFKC3zWBGzDt6dgECKY0/plJvbccwH74nNK2vD/ZzAFXMwZaQ9ZW1MewqyzsGrcQ/FNTK9JVXsOIYms1EvC89oy0v7DPm/1jVLRSwnp81uKdh3yCN65XBYt6xzKIoLiu0ze20ZJsm0dGcuz6W5NOVkXUODWo41/4Ds7aptdFeADFnHA1GyKnffp0MWWt5/L1Ed0mXdIs+WldhL3irXOHMjbYhVl/rlDLU7TimV2kv+XP4/p1HXIdUguy6xAKHCXgemhF9W1OugumSe8XlbTr1lyblK+6cYcjbZKv1Tzj4BQ8ocKh9LPeZL6J+Sp7Tstffl/1M8MYxtNCLtlwext8RYjxWlavu8ZRVdZIB0BDxNAhRV8euWQJgHInaVodmWpBPlCGiS2QjTO9r2kLY+i2btHZuarLmnZAt+czo1VXtTszX3fsxzPGWdCwxNwP8BdONh/W3ZwtIAAAAASUVORK5CYII=';var mapData = [{ name: '济南市', value: 30057 },{ name: '青岛市', value: 40057 },{ name: '淄博市', value: 50057 },{ name: '枣庄市', value: 20057 },{ name: '东营市', value: 24057 },{ name: '烟台市', value: 20057 },{ name: '潍坊市', value: 25057 },{ name: '济宁市', value: 60057 },{ name: '泰安市', value: 50057 },{ name: '威海市', value: 20057 },{ name: '日照市', value: 80057 },{ name: '临沂市', value: 28057 },{ name: '德州市', value: 20057 },{ name: '聊城市', value: 98057 },{ name: '滨州市', value: 256057 },{ name: '菏泽市', value: 204557 }
];var mapCenter = [{ name: '济南市', value: [117.000923, 36.675807] },{ name: '青岛市', value: [120.355173, 36.082982] },{ name: '淄博市', value: [118.047648, 36.814939] },{ name: '枣庄市', value: [117.557964, 34.856424] },{ name: '东营市', value: [118.66471, 37.434564] },{ name: '烟台市', value: [121.391382, 37.539297] },{ name: '潍坊市', value: [119.107078, 36.70925] },{ name: '济宁市', value: [116.587245, 35.415393] },{ name: '泰安市', value: [117.129063, 36.194968] },{ name: '威海市', value: [122.116394, 37.509691] },{ name: '日照市', value: [119.461208, 35.428588] },{ name: '临沂市', value: [118.326443, 35.065282] },{ name: '德州市', value: [116.307428, 37.453968] },{ name: '聊城市', value: [115.980367, 36.456013] },{ name: '滨州市', value: [118.016974, 37.383542] },{ name: '菏泽市', value: [115.469381, 35.246531] }
];
echarts.registerMap('山东', map);
option = {backgroundColor: '#062940',tooltip: {trigger: 'item',backgroundColor: 'rgba(0,0,0,.8)',borderColor: '#3574c8',borderWidth: '2',extraCssText: 'padding:10px;box-shadow: 0 0 3px rgba(0, 0, 0, 0.3);',show: true,formatter: function (params) {if (params.componentSubType == 'map') {return `<span style="color:#fff">${params.name}: ${params.value}</span>`;}}},visualMap: {min: 1,max: 90000,text: ['High', 'Low'],realtime: false,calculable: true,show: false,inRange: {color: ['#24439B', '#6CC5EF']}},geo: {map: '山东',layoutSize: '100%',silent: true,roam: false,z: 0},series: [{name: 'map',type: 'map',map: '山东',label: {show: true,color: 'white'},emphasis: {label: {color: '#FFDB4C'},itemStyle: {areaColor: '#e54d42'}},data: mapData},{type: 'scatter',coordinateSystem: 'geo',label: {normal: {show: true,formatter: function (params) {return '';},color: 'white'},emphasis: {show: true}},itemStyle: {color: '#00FFF6'},symbol: iconRQ,symbolSize: [50, 80],symbolOffset: [0, 0],z: 999,data: mapCenter},{type: 'scatter',coordinateSystem: 'geo',label: {normal: {show: true,formatter: function (params) {return `{a| ${params.name} } \r\n {b| echarts 可视化统计}`;},color: '#fff',rich: {a: {color: '#FFDB4C',fontSize: 16,padding: [10, 10, 5, 0],align: 'center'},b: {color: '#fff',lineHeight: 18,height: 18,align: 'left'}}},emphasis: {show: true}},itemStyle: {color: '#00FFF6'},symbol: iconLD,symbolSize: [140, 75],symbolOffset: [0, -75],z: 999,data: mapCenter}]
};
二、环形图
echarts 环形图:多层嵌套,自定义 legend 位置、颜色,中间插入数据及文字,颜色渐变;
文字链接: https://blog.csdn.net/aibujin/article/details/124796709?spm=1001.2014.3001.5501
三、k 线图
文章链接: https://blog.csdn.net/aibujin/article/details/124797924?spm=1001.2014.3001.5501
四、折线图
echarts 折线图,横纵坐标轴线颜色、文字颜色,网格线,坐标轴两侧留白,数据渐变,刻度线等;
文章链接:https://blog.csdn.net/aibujin/article/details/124802512?spm=1001.2014.3001.5501
文章链接:https://blog.csdn.net/aibujin/article/details/130157140?spm=1001.2014.3001.5501
文章链接:https://blog.csdn.net/aibujin/article/details/130223130?spm=1001.2014.3001.5501
五、横向柱状图
echarts 横向柱状图,坐标轴隐藏,网格线颜色渐变,网格默认背景,柱状图边框宽度/颜色,数据渐变,刻度线隐藏等;
文章链接: https://blog.csdn.net/aibujin/article/details/124802889?spm=1001.2014.3001.5501
六、折线图 + 柱状图
echarts 折线图 + 柱状图,左右两侧y轴线,横纵坐标轴线颜色、文字颜色,网格线,坐标轴两侧留白,数据渐变,刻度线等;
文章链接: https://blog.csdn.net/aibujin/article/details/124803493?spm=1001.2014.3001.5501
七、3D 柱状图
echarts 3D 柱状图,多个柱状图叠加,y轴内刻度线、隐藏横坐标,文字颜色,网格线,坐标轴两侧留白,数据渐变,刻度线等;
文章链接: https://blog.csdn.net/aibujin/article/details/124879825?spm=1001.2014.3001.5501
八、工程项目可视化
echarts 工程项目可视化,依据x轴时间坐标轴,叠加展示不同阶段的项目节点,y轴展示项目阶段名、文字颜色,网格线,坐标轴两侧留白、背景色等;
文章链接: https://blog.csdn.net/aibujin/article/details/130237643?spm=1001.2014.3001.5501
九、雷达图
echarts 雷达图,自定义指示器名称,线条样式、区域填充样式、折线拐点标志、自定义名称样式、坐标轴分隔线、坐标轴两侧留白、背景色等;
文章链接:https://blog.csdn.net/aibujin/article/details/130266382?spm=1001.2014.3001.5501
十、象形柱图
echarts 象形柱图,隐藏横纵坐标轴、网格线,坐标轴两侧留白,自定义矢量图,文字提示框、图形类型、背景色等;
文章链接:https://blog.csdn.net/aibujin/article/details/130289101?spm=1001.2014.3001.5501
十一、环形占比图
echarts 环形占比图,环形图、仪表盘、刻度线,自定义提示框、颜色渐变、背景色等;
文章链接:https://blog.csdn.net/aibujin/article/details/130265744?spm=1001.2014.3001.5501
十二、圆环动画
echarts 圆环动画,饼图、环形图、图表动画、网格线,颜色渐变,图行矢量,文字提示框、图表层级、背景色等;
文章链接:https://blog.csdn.net/aibujin/article/details/130288849?spm=1001.2014.3001.5501
十三、地图 json 免费下载
-
全省份 json 下载:https://mp.csdn.net/mp_download/manage/download/UpDetailed?spm=3001.5299
-
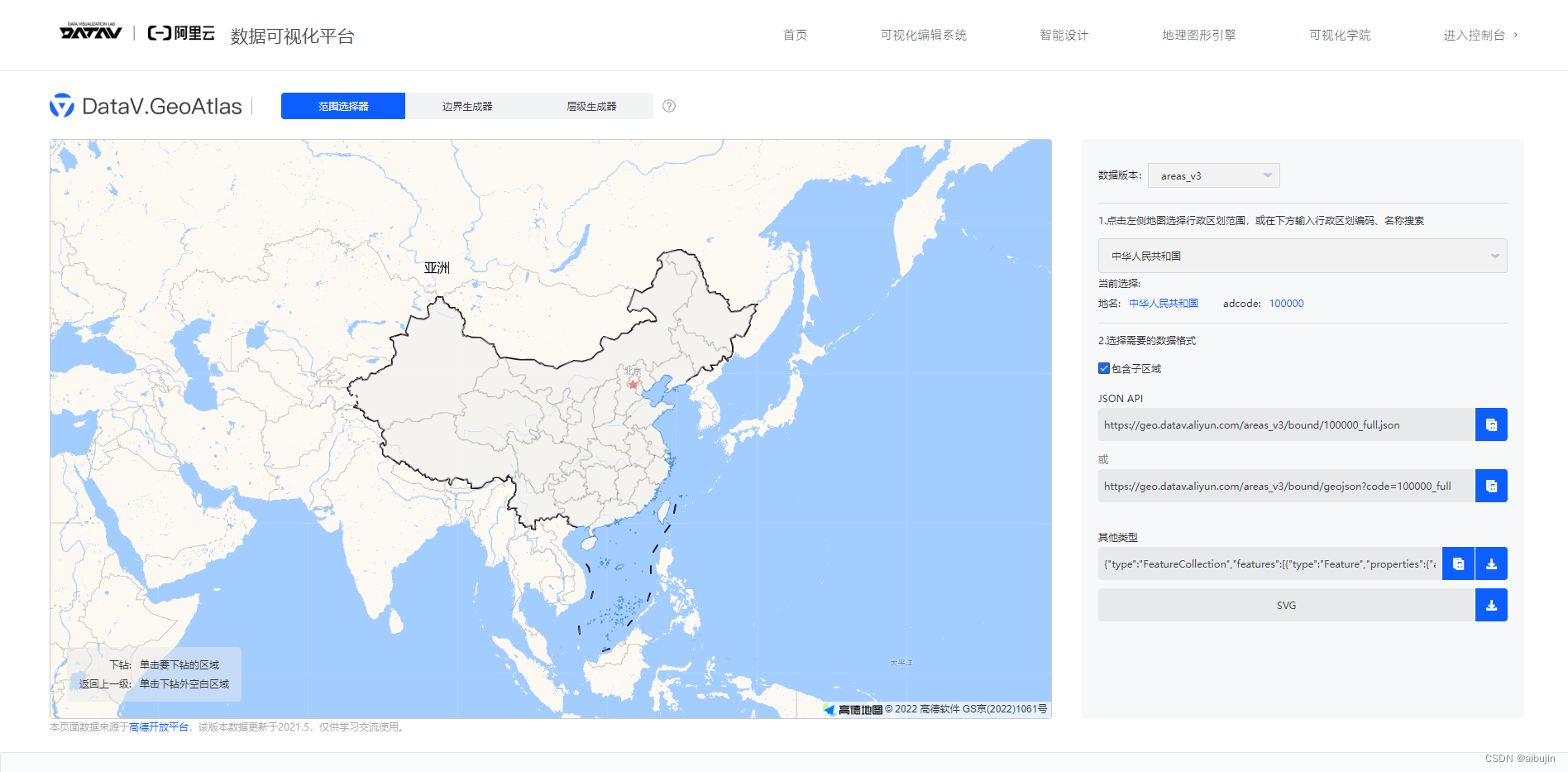
阿里数据可视化平台下载:http://datav.aliyun.com/portal/school/atlas/area_selector
3. https://geojson.cn/




![[转]使用Modernizr 检测HTML5和CSS3浏览器支持功能](http://wwwimages.adobe.com/www.adobe.com/content/dam/Adobe/en/devnet/dreamweaver/articles/using-modernizr/fig09.jpg)
