文章和代码已经归档至【Github仓库：https://github.com/timerring/algorithms-notes 】或者公众号【AIShareLab】回复 算法笔记 也可获取。

Trie树（字典树）

Trie树是用来快速存储和查找 字符串集合的数据结构。某个字符串集合对应的有根树。树的每条边上对应有恰好一个字符，每个顶点代表从根到该节点的路径所对应的字符串（将所有经过的边上的字符按顺序连接起来）。利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希树高。

基本思想

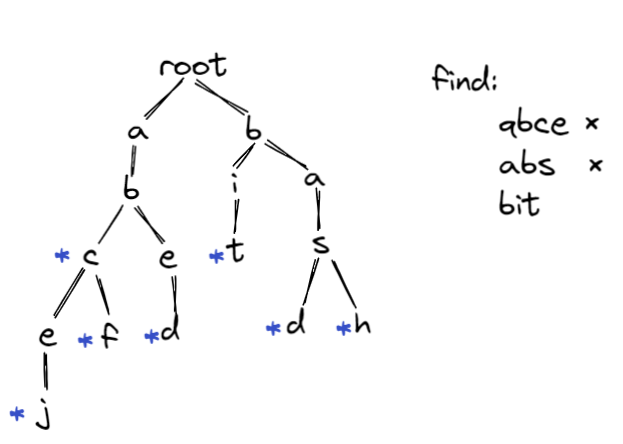
存储若干字符串（通常样本中的字符较少），然后根据字符串中字符出现的先后顺序建立树，把具有相同前缀的字符串按照其前缀归类在一个分支中，并且需要在字符串的最后一个位置进行标记（表明到此为一个完整的字符串）。

查找时只需要寻找是否有匹配的序列，并且是否已标记结尾即可。

例题 Trie字符串统计

维护一个字符串集合，支持两种操作：

1. I x 向集合中插入一个字符串 x；
2. Q x 询问一个字符串在集合中出现了多少次。

共有 N 个操作，输入的字符串总长度不超过 $10^5$，字符串仅包含小写英文字母。

输入格式

第一行包含整数 N，表示操作数。

接下来 N 行，每行包含一个操作指令，指令为 I x 或 Q x 中的一种。

输出格式

对于每个询问指令 Q x，都要输出一个整数作为结果，表示 x 在集合中出现的次数。

每个结果占一行。

数据范围

$1\le N\le 2\ast 10^4$

输入样例：

5
I abc
Q abc
Q ab
I ab
Q ab

输出样例：

1
0
1

code

#include<iostream>
using namespace std;const int N = 100010;
// 下标0代表根节点和空节点，cnt用于计数，idx代表当前的节点（和单链表一样）相当于是一个独一无二的递增编号，son[N][26]每个节点最多有26条边（小写英文字母）
int son[N][26], cnt[N], idx;
char str[N];
// 插入
void insert(char str[])
{int p = 0;// 根节点// 遍历字符串，cpp中str最后一位是\0for(int i = 0; str[i]; i ++){// 映射字母a-z为0-25int u = str[i] - 'a';// 若不存在该节点则创建一个if(!son[p][u]) son[p][u] = ++ idx;// 走到该子节点p = son[p][u];}cnt[p] ++ ;// 标记该子节点存在的单词个数 记住这里p = son[p][u];
}
// 查询
int query(char str[])
{int p = 0;for(int i = 0; str[i]; i++){int u = str[i] - 'a';if(!son[p][u]) return 0;p = son[p][u];}return cnt[p];
}int main()
{//ios::sync_with_stdio(false);//cin.tie(0);int n;scanf("%d", &n);while(n --){char op[2];scanf("%s%s", op, str);if(op[0] == 'I') insert(str);else printf("%d\n", query(str));}return 0;
}

关于idx的理解

不管是链表，Trie树还是堆，他们的基本单元都是一个个结点连接构成的，可以成为“链”式结构。这个结点包含两个基本的属性：本身的值和指向下一个结点的指针。按道理，应该按照结构体的方式来实现这些数据结构的，但是做算法题一般用数组模拟，主要是因为比较快。

原来这两个属性都是以结构体的方式联系在一起的，现在如果用数组模拟，如何才能把这两个属性联系起来呢，如何区分各个结点呢？答案是采用idx。

idx的操作总是 idx++，这就保证了不同的idx值对应不同的结点，这样就可以利用idx把结构体内两个属性联系在一起了。因此，idx可以理解为结点。

idx相当于一个分配器，如果需要加入新的结点就用++idx分配出一个下标,输入字符串的总长度不超过$10^5$，因此最多会用到$10^5$个idx。

Trie树中有个二维数组 son[N][26]，表示当前结点的儿子，如果没有的话，可以等于++idx。Trie树本质上是一颗多叉树，对于字母而言最多有26个子结点。所以这个数组包含了两条信息。比如：son[1][0]=2表示1结点的一个值为a的子结点为结点2;如果son[1][0] = 0，则意味着没有值为a子结点。这里的son[N][26]相当于链表中的ne[N]。当然这里2仅仅是一个节点的编号而已。

参考：https://www.acwing.com/solution/content/5673/

模板总结

int son[N][26], cnt[N], idx;
// 0号点既是根节点，又是空节点
// son[][]存储树中每个节点的子节点
// cnt[]存储以每个节点结尾的单词数量// 插入一个字符串
void insert(char *str)
{int p = 0;for (int i = 0; str[i]; i ++ ){int u = str[i] - 'a';if (!son[p][u]) son[p][u] = ++ idx;p = son[p][u];}cnt[p] ++ ;
}// 查询字符串出现的次数
int query(char *str)
{int p = 0;for (int i = 0; str[i]; i ++ ){int u = str[i] - 'a';if (!son[p][u]) return 0;p = son[p][u];}return cnt[p];
}

应用 最大异或对

在给定的 N个整数 $A_1$，$A_2$……$A_N$ 中选出两个进行 $xor$（异或）运算（一般异或运算是按位计算的），得到的结果最大是多少？

输入格式

第一行输入一个整数 N。

第二行输入 N 个整数 $A_1$～$A_N$。

输出格式

输出一个整数表示答案。

数据范围

$1\le N\le 10^5$
$0\le A_i<2^{31}$

输入样例：

3
1 2 3

输出样例：

3

分析

首先是暴力做法BF $O(n^2)$：

for (int i = 0; i < n; i++)
{for (int j = 0; j < i; j++){// 但其实 a[i] ^ a[j] == a[j] ^ a[i], 所以内层循环 j < i // 因为 a[i] ^ a[i] == 0 所以事先把返回值初始化成0 不用判断相等的情况}
}

异或也可以理解为不进位加法，相同的话异或值为0。Trie树不仅可以存储整数，也可以存储二进制数。而计算机中所有文件都是以二进制的形式保存的，换句话说Trie数可以存储任何文件。异或后最大，这需要寻找出与原数每位不同的数，为保证最大值，需要从最高位开始依次寻找，过程如下所示：

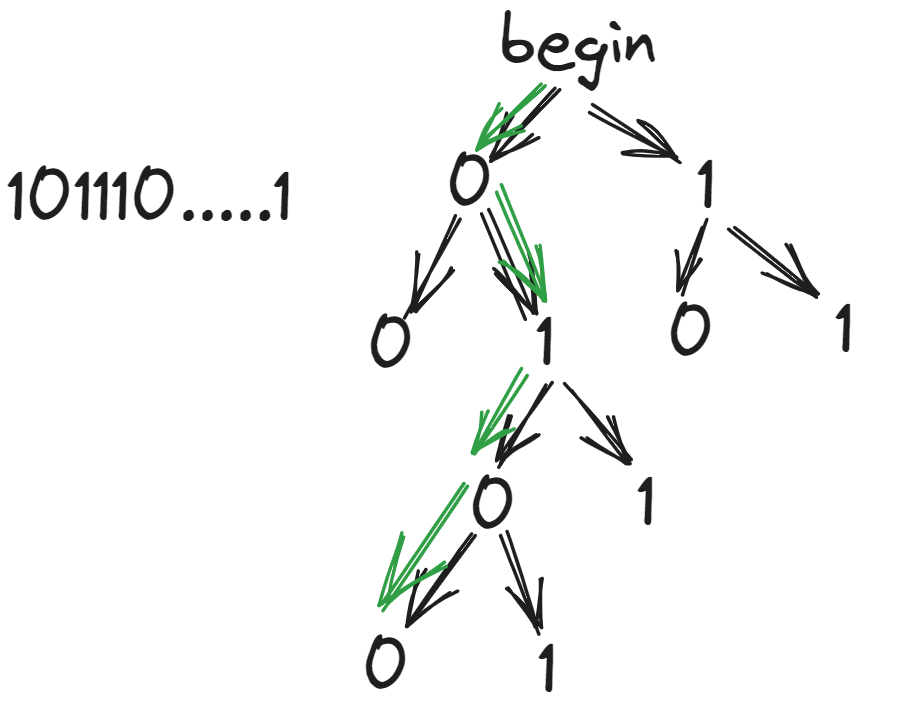
可以不用先全部插入，因为这是有顺序的，避免多次枚举 $a_j$ 和 $a_i$ 以及 $a_i$ 和 $a_j$ 的情况。因此可以先查找再插入（可能最开始的情况下要写一个特判,因为最开始没有可以查找的内容），当然也可以先插入再查找（可能存在的问题就是每次自己和自己异或是0，没有意义）。

#include <iostream>
#include <algorithm>using namespace std;
// N是整数个数，M是树的总宽度
const int N = 100010, M = 3100010;int n;
int a[N], son[M][2], idx;void insert(int x)
{int p = 0;for (int i = 30; i >= 0; i -- ){// 从高到低依次取每一位int u = x >> i & 1;// 没有该节点则插入该节点if (!son[p][u]) son[p][u] = ++ idx;// 指针指向下一层p = son[p][u];}
}int query(int x)
{int p = 0, res = 0;for (int i = 30; i >= 0; i -- ){// 从最大位开始找int u = x >> i & 1;// 如果当前层有对应的不相同的数,p指针就指到不同数的地址if (son[p][!u]){p = son[p][!u];// 因为这一位不同，异或后为1，这里向前移位并且保留相反数即可。res = res * 2 + !u;}else {p = son[p][u];// 如果没有相异的数，则只能向前移一位然后保留该数即可。res = res * 2 + u;}}return res;
}int main()
{scanf("%d", &n);for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);int res = 0;for (int i = 0; i < n; i ++ ) {insert(a[i]);int t = query(a[i]);// 最后再进行异或处理res = max(res, a[i] ^ t);}printf("%d\n", res);return 0;
}

同时，这里关于代码有两个思路，一个是上面这种query需要寻找的对应的异或的整数，最后 max(res, a[i] ^ t) 得到结果。

此外还可以直接在 query 中提前进行比较计算，最后直接比较结果即可 max(res, t)，过程如下：

int query(int x)
{int p = 0, res = 0;for (int i = 30; i >= 0; i -- ){// 从最大位开始找int u = x >> i & 1;// 如果当前层有对应的不相同的数,p指针就指到不同数的地址if (son[p][!u]){p = son[p][!u];// 因为这一位不同，异或后为1，只需要向前移并且加1即可res = res * 2 + 1;}else {p = son[p][u];// 这一位相同，xor后为0，向前移一位然后置0即可。res = res * 2 + 0;}}return res;
}