论文研读-用于约束多目标优化的新型双阶段双种群进化算法

A Novel Dual-Stage Dual-Population Evolutionary Algorithm for Constrained Multi-Objective Optimization

觉得有用的话,欢迎一起讨论相互学习~

我的微博我的github 我的B站

最近我在学习约束多目标问题的论文，其中由明博士和张教授发表在TEVC上的DD-CMOEA非常不错~
原文链接
此篇文章为 M. Ming, R. Wang, H. Ishibuchi and T. Zhang, "A Novel Dual-Stage Dual-Population Evolutionary Algorithm for Constrained Multi-Objective Optimization," in IEEE Transactions on Evolutionary Computation, doi: 10.1109/TEVC.2021.3131124. 的论文学习笔记，只供学习使用，不作商业用途，侵权删除。并且本人学术功底有限如果有思路不正确的地方欢迎批评指正！

Abstract

除了寻找可行的解决方案之外，利用信息丰富的不可行解决方案对于解决受约束的多目标优化问题 (CMOP) 也很重要。然而，大多数现有的受约束的多目标进化算法（CMOEA）无法有效地探索和利用这些解决方案，因此在面临大的不可行区域的问题时表现出较差的性能。为了解决这个问题，本文提出了一种称为 DD-CMOEA 的新方法，该方法具有双重阶段（即探索和开发）和双重种群。具体来说，称为 mainPop 和 auxPop 的两个种群首先在考虑和不考虑约束的情况下单独进化，分别负责探索可行和不可行的解决方案。然后，在开发阶段，mainPop 提供有关可行区域位置的信息，这有助于 auxPop 找到并利用周围的不可行解决方案。 auxPop 获得的有希望的不可行解决方案反过来帮助 mainPop 更好地收敛到帕累托最优前沿。对三个知名测试套件的广泛实验和一个真实案例研究充分表明，DD-CMOEA 比五个最先进的 CMOEA 更具竞争力。
关键词：Constrained multi-objective optimization problems, exploration, exploitation, coevolution.

Introduction

首先是一段CMOPs和CMOEAs的解释和定义
与无约束的多目标优化问题 (MOP) 相比，CMOP 更具挑战性。具体而言，CMOP 的约束可以使搜索/目标空间的很大区域不可行，将目标空间划分为狭窄的不连通可行区域，和/或使相应的无约束 MOP 的 PF 部分或完全不可行 [4] .因此，PF 可能会断开并位于约束边界上，导致难以获得所需的解集
在过去的二十年里，为了解决 CMOPs，人们投入了大量精力来开发约束多目标进化算法 (CMOEAs)，并与约束处理技术相结合。大多数早期的 CMOEA，如 C-NSGA-II [5]，首先将人口尽快推向可行区域，然后考虑优化可行区域内的目标。这可能使种群容易落入一些局部最优区域，如图 1 所示。
为了解决这个问题，一些研究人员致力于在搜索过程中保留不可行的解决方案，并从不可行的解决方案中提取有用的遗传信息，以产生更多样化的解决方案。沿着这条研究路线，已经提出了许多 CMOEA 来利用不可行的解决方案。例如，C-TAEA [7]、ISC-NSGA-III [8]、PPS-MOEA/D [9]、ToR-NSGA-II [10] 和 CCMO [11]。他们被证明在许多测试问题上具有竞争力。他们中的一些更喜欢探索不可行的解决方案来寻找具有更好客观价值的解决方案，而另一些人则更喜欢在约束边界附近利用不可行的解决方案。由于探索和开发都很重要，偏向其中之一很容易导致无法获得完整的 PF，尤其是当 CMPOP 具有较大的不可行区域时。然而，到目前为止，这个问题很少被研究。（Motivation）
在本文中，我们考虑了对不可行解决方案以及可行解决方案的探索和利用。此外，我们同时使用协作和互补的种群（即 mainPop 和 auxPop），它们在探索和开发阶段扮演不同的角色。所提出的基于双阶段和双种群的算法（称为DD-CMOEA）的主要新颖特征如下：

进化过程包括探索和开发阶段。当 auxPop 的收敛趋于平稳时，就会发生从探索到开发的阶段转换。
在探索阶段，mainPop 旨在寻找可行区域并保存可行的解决方案；而 auxPop 在不考虑任何约束的情况下探索整个搜索空间，并保留具有良好目标值的解决方案，无论可行性如何。在这个阶段，auxPop 是前向搜索的主力，引导 mainPop 穿过不可行区域。
在开发阶段，mainPop 继续从可行端向 PF 移动，同时将 auxPop 从不可行端引导向 PF。由于提出的牵引策略，auxPop 可以在 PF 附近快速找到有希望的不可行解（具有良好的目标值和低约束违规），从而帮助 mainPop 更好地收敛。
两个种群之间的合作不仅在于在后代产生过程中交换信息，而且还发生在一个种群提供信息以指导另一个种群的移动时。

本文的其余部分安排如下。在第 II 节中，介绍了文献综述和提出的 DD-CMOEA 的动机。第三节详细介绍了提出的 DD-CMOEA。随后，在第四节和第五节中，对 DD-CMOEA 的竞争力进行了全面调查，并在 36 个基准问题和一个真实世界的 CMOP 上与五个最先进的 CMOEA 进行了比较。第六节给出了结论和未来的研究方向。

2.Backgound

2.1 Literature Review

2.1.1 单种群算法

在文献中，已经提出了大量的约束处理技术来解决 CMOP。其中，最简单的技术是面向可行性的方法[5]、[12]。代表是约束支配原则（CDP）嵌入式算法，如C-NSGA-II [5]和C-MOEA/D [13]。顾名思义，他们强烈喜欢可行的解决方案而不是不可行的解决方案。这种偏好可以促进种群快速进入可行域，但容易导致过早收敛。
为了解决这个问题，许多研究人员一直致力于不可行辅助方法。一般的想法是从不可行的解决方案中提取信息，以帮助可行的解决方案的演变。早期开发的技术主要包括：i）基于惩罚函数的方法[14]，ii）随机排序[15]，iii）α-约束方法[16]，以及iv）基于多目标优化的方法[17]。然而，前三组需要仔细调整参数以实现可行和不可行区域之间的平衡搜索。第四组可能在寻找可行算法上花费的精力不足，而且会导致算法计算复杂度的增加。尽管这些技术的组合可以增强算法的能力，但需要为每种采用的技术指定适当的参数值[18]。
为了更好地利用可行和不可行的解，最近提出了一些新的不可行辅助方法，例如混合排序方法和两阶段机制。例如，Ning等人。建议根据其帕累托等级和约束等级[19]为每个解决方案分配一个等级编号。 ToR-NSGA-II [10] 使用了一种新的适应度函数，它根据两个排名的加权和来评估每个解决方案的适应度。一种排名基于 CDP（类似于 C-NSGA-II [5]），另一种基于帕累托优势关系，不考虑约束。对于两阶段算法，一个代表是 PPSMOEA/D [9]，它将搜索过程分为推拉阶段。具体来说，它使用 MOEA/D [20] 来探索搜索空间，而不考虑第一阶段的任何约束。然后，在第二阶段，采用改进的 α-约束方法来动态调整违反约束的松弛值，旨在将解拉近可行区域。在另一个名为 ToP [21] 的两阶段框架中，第一阶段通过将 CMOP 转换为单目标问题来找到有希望的可行区域，第二阶段通过特定的 CMOEA 获得最终解决方案。此外，还设计了一些新算法，例如 C-MOEA/DD [22] 和 ISC-NSGA-III [8]，以强调选择与孤立子区域相关的不可行解决方案。

2.1.2 合作协同算法

受协同进化机制在其他领域（如大规模优化[23]）成功的启发，一些研究人员试图开发协同进化算法来解决 CMOP。例如，Wang等人提出了一个合作差分进化框架（命名为CCMODE [24]）。它借用了 CMODE [25] 的协同进化思想来协同进化 m 个子群体和一个档案群体，以解决受约束的 m 目标优化问题。在 CCMODE 中，每个子群体只需要优化一个指定的目标。最近，为 CMOPs 提出了一种竞争性的两档案共同进化 CMOEA，名为 C-TAEA [7]。在 C-TAEA 中，一个档案（名为 CA）保持收敛性和可行性，而另一个档案（名为 DA）通过探索 CA 开发不足的领域来促进多样性。更新机制是 NSGA-II [5] 中的非支配排序和 MOEA/D-M2M [26] 中的密度估计的组合。在 [11] 中，提出了一种基于两个群体的共同进化框架，称为 CCMO，其中一个群体解决 CMOP，而另一个群体解决其无约束版本。 CCMO 中两个种群之间的合作比其他 CMOP 的协同进化算法（例如，CCMODE [24]）要弱得多。
总而言之，这些现有 CMOEA 的特点和缺点如补充文件的表 I 所示。

2.2 Motivation

尽管文献中的不可行辅助 CMOEA（例如，C-TAEA [7] 和 CCMO [11]）在某些 CMPOP 上表现出良好的性能，但在遇到复杂约束时仍然面临困难，部分原因是对不可行解决方案的利用有限。如图 2 所示，不可行的解决方案应根据问题采用不同的方式。具体来说，在图 2（a）中，具有良好目标值的不可行解可用于通过不可行区域（参见 A 和 B）。在这种情况下，需要通过将当前不可行的解决方案向前（左下方向）拉来寻找具有更好目标值的新可行解决方案。另一方面，在图 2（b）中，不可行的解决方案可用于从不可行的一侧接近真实的 PF（参见 C 和 D）。在这种情况下，需要通过将当前不可行的解决方案拉向约束边界（在右上方向）来找到具有较小约束违规的新解决方案。
因为真实PF的位置时未知的，因此我们需要以这两种方式谨慎地利用不可行的解决方案。否则，就会缺乏适应不同问题的能力。例如，尽管积极的前向探索有助于图 2(a) 中的搜索，但它可能会导致如图 2(b) 中的无约束 PF 的许多不可行的解决方案。相比之下，在约束边界附近仔细利用不可行的解决方案将减缓种群向图2（a）中真实 PF 前进。然而，现有的不可行辅助 CMOEA 很少有能力处理这两种类型的不可行解决方案。因此，设计一种新颖的机制非常重要，该机制在探索具有更好目标值的不可行解决方案（如图 2（a））和利用约束边界附近的不可行解决方案（如图 2（b））之间取得良好平衡。
出于上述考虑，我们建议使用进化不可行解的辅助种群（称为 auxPop）作为主要种群（称为 mainPop）的补充。 mainPop 负责发展和维护好的可行解。 auxPop 首先探索整个搜索空间，然后在 mainPop 的指导下，转向利用真实 PF 附近的不可行解决方案。设计了一种基于双阶段和双种群的算法，以充分利用不可行解决方案中的信息，从而引导搜索到有希望的区域并有效地找到好的可行解决方案。所提出算法的详细信息在第三节中介绍

3.PROPOSED ALGORITHM: DD-CMOEA

3.1 Outline of DD-CMOEA

其中算法流程图如图3所示，需要注意的是mainPop的选择策略在两个阶段相同，但是auxPop的选择策略在前后两个阶段不同，在Exploration阶段使用目标函数值，在Exploitation阶段使用牵引策略。
所提出的算法有两个种群：一个主要种群（称为 mainPop）和一个辅助种群（称为 auxPop）。 mainPop 始终根据独立于搜索阶段的可行性规则进行更新，并从可行区域向真实 PF 移动。 auxPop 在探索阶段寻找无约束的 PF，在开发阶段，在 mainPop 的引导下，从无约束的 PF 向真实的 PF 移动。最终的 mainPop 是所提出算法的输出。
算法1给出了DD-CMOEA的伪代码，每个种群具有相同的种群大小N，一开始，mainPop 被随机初始化并复制到 auxPop。在初始化之后，进化经历了探索和利用阶段。这两个阶段在第 III-B 节和第 III-C 节中进一步详细解释，其中 SPEA2 [27] 被用作基本优化器。原则上，DD-CMOEA 可以嵌入到任何 MOEA 中。 DDCMOEA中的交配选择策略和遗传算子由所使用的MOEA决定。

3.2 Exploration Stage

探索阶段的主要目的是广泛寻找具有良好目标值的解决方案。一个简单的想法是在此搜索过程中暂时忽略约束，以避免受到不可行障碍的阻碍。同时，我们期望发展出一系列可行的解决方案。因此，在探索阶段，auxPop 的设计目的是不考虑任何约束向前推进，而 mainPop 则是根据可行性规则CDP寻找好的解决方案。接下来，逐步解释实现细节。
1） Reproduction procedure:分为选择性交配和子代生成过程。父代分别从mainPop和auxPop中选择，每个父代集生成N/2的新解，使用SBX[28]和多项式变异[29].
2） Update Procedure:生成子代后使用不同的环境选择策略对两个种群进行更新。
在 mainPop 中，可行的解决方案总是被认为比不可行的解决方案更好，因此使用可行性规则来更新 mainPop。在第 7 行将后代种群与 mainPop 结合后，根据它们的约束违反和目标值比较解决方案。一个解 x1 被称为约束支配另一个解 x2： i) 如果两个解不可行并且 x1 更少违反约束； ii) 如果 x1 可行而 x2 不可行；或 iii) 如果两个解决方案是可行的（或具有相同的约束违反值）并且 x1 在其目标值方面优于 x2。（请注意，两个解具有相同约束违反值的情况很少见，尤其是当约束由连续函数定义时。）每个解的适应度可以根据它们的约束-支配关系和密度在 SPEA2 [27] 中计算目标函数中携带的信息。详见[27]。接着CPt1中的所有个体根据他们的适应度函数进行排序，并挑选出N个解组成新的mainPop如第8行所示。
在auxPop中，更偏好具有良好目标值的解。在auxPop和子代种群合并之后，不用考虑任何约束，N个具有最好适应度的个体被保留在auxPop中直到下一个世代。
注意： 正如我们所解释的，mainPop 和 auxPop 具有不同的环境选择策略。因此，他们可以在遇到不可行区域时存储不同类型的解决方案，而不管问题类型如何。注意问题的分类可以参考第四节。限于篇幅，仅以类型IV的两个问题为例来说明探索过程。如图 4 和图 S-13 所示，auxPop 可以搜索具有良好目标值的解，并逐渐逼近无约束的 PF。另一方面，mainPop 存储在探索过程中找到的良好可行的解决方案。
3） Decision of Search Stage:在auxPop更新后，auxPop的改进会通过量化的方式进行考量以判断auxPop是否进入一个稳定的状态。如在[9]中所述，种群的改进程度可以通过考量种群中特定点经过一定世代后的改变率来考量。例如理想点和最低点。在这篇文章中，平均点，估计理想点和估计最低点被用作表征目标向量分布的特征点。以下的计算方法是取每个目标上平均点，理想点，最低点的最大值作为ra,rz,rn,然后比较ra,rz,rn，取这三个数中的最大值作为衡量种群的变化率rt,其中t表示迭代的次数。其中l_gap表示世代的gap,用以计算rt.更多的需要参考补充材料中的详细描述。
由于严格的切换条件，除了一些非常复杂的情况外，几乎所有情况下，在探索阶段结束时，auxPop 都位于无约束 PF 附近。在无约束 PF 和真实 PF 相同的问题中，mainPop 和 auxPop 在切换点处接近真实 PF。然而，在其他类型的问题中（无约束的PF和真实的PF不同），auxPop中的解具有很好的客观价值，但很可能是不可行的，甚至与真实的PF相距甚远；另一方面，mainPop 中维护的解决方案是可行的或具有较低的约束违反值，而它们的目标值仍然需要改进。很明显，这两个种群的特征是互补的，特别是在无约束 PF 和真实 PF 不同的问题的情况下。

3.3 Exploitation Stage

mainPop 和 auxPop 旨在在开发阶段协同收敛到真正的 PF。设计目的如下：在无约束PF和真实PF相同的问题下，两个种群可以继续合作寻找具有更好目标值的解；对于两个 PF 不同的问题，mainPop 和 auxPop 可以分别从可行侧和无约束 PF 向真实 PF 移动。在这个过程中，mainPop 向 auxPop 提供了真实 PF 的大致位置信息，使 auxPop 能够利用真实 PF 附近的不可行方案。 auxPop 中保留的好的不可行解决方案反过来帮助 mainPop 优化目标。
算法 1 的第 19-30 行介绍了 DDCMOEA 在开发阶段的操作。在这个阶段的开始，一个引导种群Pg,用于引导auxPop种群，并且在每次开发的过程中，在第28行中使用算法2和牵引策略进行更新。
牵引策略的设计目的是有效地找到跨越真实 PF 附近不同子区域的有希望的不可行解决方案。如图5所示，在开发阶段，每个解都会被分割到一个子域中，域的数量由auxPop中解的数量决定，即auxPoP中的每个解都会被分解到一个单独的子域中。此外，在 MW9 上运行所提出的具有真实种群（100 个个体）的算法，以展示其在开发阶段的三个阶段中的性能，如图 S-2 所示。请注意，在开发阶段的 auxPop 中使用了一组权重向量，其指定方式与 MOEA/D [20] 中相同。第 i 个子区域定义如下 [22]：
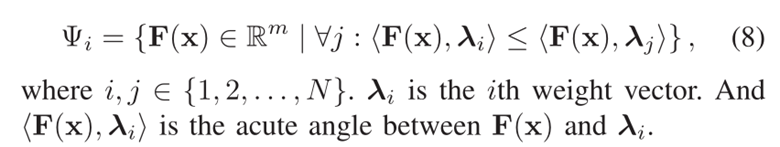
算法2概述了开发阶段对于auxPop和guide-population的引导策略的步骤. 最初，原始的 guide-population 与新的 mainPop 合并到第 1 行中的联合群体中，表示为 Pjoint，从中为每个子区域选择一个新的 guide-solution。然后遍历所有子区域的循环更新 guide-population 和 auxPop（第 3-18 行）。处理每个子区域的过程进一步分为两个步骤。
首先确定对于每个子域的引导解guide-solution (line 4-10), 从合种群中挑选子区域中的解，表示为Ai. 如果Ai是一个空的集合，就从Pjoint中挑选离第i个权重向量最近的解进入Ai集合中。并且Ai集合中具有最小约束违反的解被挑选出来作为候选解集Gi. 在候选解集Gi中的中具有最小gTE值的解被挑选出来作为第i个子区域中的引导解，表示为xi*，随后，xi* 被收入到引导种群Pg中。
注意： gTE是根据改进切比雪夫方法计算的标量方法，由公式（9）定义。
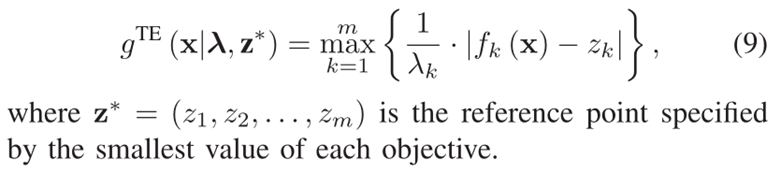
第二个步骤是更新第i个子域中的auxPop中的解（line11-17）.xi被用来引导auxPop在第i个子域中的更新。首先，我们根据公式（8），将auxPop和子代的合种群CP2t中第i个子域对应的解挑选出来并存档到Bi中。然后，Bi中具有更小的gTE值的解被挑选出来放进种群Hi中。如果Hi是一个空集，xi被放进新的auxPop种群中。否则，具有最小约束的解从候选解集Hi中选出并添加到新的auxPop中。这个过程如图6所示，其中Bi这个种群中有三个解分别是xb1,xb2,和xb3. Xb2和xb3相比于xi*来说具有更好的gTE值，因此他们都被选择进入到Hi中。然后xb2作为最优秀的解被挑选进auxPop中，以其最小的约束违反值。
这样，在每个子区域中选择到 auxPop 中的解决方案具有比在相关子区域中找到的最佳可行解决方案更好（或可比较）的目标值，并且还具有低（或零）约束违规。
备注： mainPop 不仅演化出可行的解决方案，还方便了guide-population 的更新。在 guide-population 的帮助下，auxPop 中的解决方案能够在不同的子区域中朝着真正的 PF 移动。

3.4 Discussion

在本小节中，我们解释了所提出的 DD-CMOEA 与两个相关算法，即 PPS-MOEA/D [9] 和 CCMO [11] 之间的异同。
和PPS-MOEA/D进行比较
相同处：DD-CMOEA和PPS-MOEA/D的相同处，他们都将搜索过程分为两个阶段，并首先考虑搜索不受约束的 PF，然后将解拉向真正的 PF。
不同处：1. PPS-MOEA/D 仅使用一个种群，并将大部分搜索工作花费在不可行的解决方案上。当在搜索过程中找到可行的解决方案时，它们会被简单地归档。相比之下，DD-CMOEA 使用一个种群（即 mainPop）来演化可行的解决方案，并使用另一个种群（即 auxPop）来寻找好的不可行的解决方案。

PPS-MOEA/D 通过不断调整约束的松弛来控制无约束 PF 和真实 PF 之间的搜索，这取决于某些参数。在 DD-CMOEA 中，由于提出的牵引策略和 mainPop 提供的信息，auxPop 在开发阶段被迅速拉到真实 PF 附近的区域。
PPS整个过程在基于分解的框架中执行，DD-CMOEA除了在开发阶段使用基于分解的框架的辅助种群外，均使用基于Pareto优势的框架。
和CCMO进行比较

相同点： 两个都使用两个种群，并且都使用合作协同的模式
不同点：

CCMO 中两个种群的搜索目标在整个进化过程中保持不变。然而，DDCMOEA 中的 auxPop 首先旨在搜索不受约束的 PF（在探索阶段），然后旨在朝着真正的 PF 迈进（在开发阶段）。因此 DD-CMOEA 可以利用不同类型的信息不可行的解决方案。
在 CCMO 中，两个种群之间的合作只能通过共享后代来实现。 DD-CMOEA 不仅在两个种群之间共享后代，而且还从 mainPop 中获取信息来指导 auxPop 的进化。
CCMO 没有额外的机制来提高多样性。在 DD-CMOEA 中，由于在牵引策略中使用权重向量，auxPop 中的解决方案可以分布在不同的子区域，有助于增强多样性

3.5 Time and Space Complexity of DD-CMOEA

分别使用 N、m、n 和 Tmax 来表示种群大小、目标数、决策变量向量的维数和最大迭代次数

4.EXPERIMENTAL STUDY

在本节中，我们首先介绍用于基准测试的测试套件和最先进的 CMOEA。然后我们测试了DD-CMOEA在不同场景下的表现。之后，将 DD-CMOEA 在三个测试套件上与最先进的 CMOEA 进行比较。最后，讨论了DD-CMOEA对参数的敏感性。

4.1 Benchmark Problems and Parameter Settings

为了系统地验证 DDCMOEA 的有效性，采用三组基准问题来比较 DD-CMOEA 与其他最先进的 CMOEA。这三个测试套件是 CTP [30]、MW [4]、LIRCMOP [6]。具体来说，CTP 是流行的 CMOP 测试套件之一。它包括具有不同类型 PF 的 CMOP，例如断开的 PF、真正的 PF 作为其不受约束的 PF 的一部分，等等。 MW 是最近提出的一个测试套件，它涵盖了各种特性，例如小可行性比、非线性约束、不同的收敛困难、不同几何形状的约束 PF 等 [4]。 LIRCMOP 测试套件的主要特点是大的不可行区域以及位置和距离变量之间的复杂联系。
根据非约束PF和真实PF的不同关系，这些问题可以分为四类 [4]
[4] Z. Ma and Y . Wang, “Evolutionary constrained multiobjective optimization: Test suite construction and performance comparisons,” IEEE Trans. Evol. Comput., vol. 23, no. 6, pp. 972–986, 2019.
以下是各种对比算法的参数设置，并且所有算法都在platEMO上实现。

4.2 Investigation into the Search Behavior of DD-CMOEA

4.2.1 Investigation into the Effect of Using Dual Populations

在本案例研究中，我们彻底调查了 DD-CMOEA 中双重群体在一些不同测试问题上的行为。这里选择 LIRCMOP6、CTP7、MW7 和 LIRCMOP1 作为示例，它们分别是 Type-I、II、III 和 IV 问题的代表性测试实例。
图 7 显示了在所提出的 DD-CMOEA 对测试问题的单次运行中，mainPop 和 auxPop（种群大小：100）中可行解决方案的数量。此运行是从 31 个运行中选择的，具有中间 IGD 值。从探索阶段到开发阶段的切换点也如图 7 所示。从图 7 中，我们可以得到以下观察结果。

i) mainPop 一旦进入可行区域，在整个演化过程中几乎不会保留任何不可行的解决方案。相比之下，auxPop 可以在整个进化过程中保持不可行的解决方案。即mainPop是以可行性为导向的，主要侧重于探索可行区域。另一方面，auxPop 可以广泛保留不可行的解决方案，从而探索不可行的区域。就搜索空间的探索而言，这两个种群在本质上是互补的。
ii) auxPop 中可行解决方案的数量随迭代次数而变化，并且因问题而异，具体取决于可行和不可行区域的几何形状。对于图 7 中的所有问题，我们可以观察到，在切换点之前 auxPop 中可行解的数量变化很小。这是因为当检测到 auxPop 中解的收敛稳定性时，搜索阶段会发生变化。
iii) 切换后 auxPop 中可行解的数量有所增加。这是因为 auxPop 开始从不受约束的 PF 向真正的 PF 移动。尽管如此，对于 Type-II、III 和 IV 问题，即图 7(b)-(d) 中的 CTP7、MW7 和 LIRCMOP1，auxPop 即使在演化的后期仍然有许多不可行的解决方案，旨在利用接近真实 PF 的不可行解所携带的有用信息。
为了进一步研究这两个群体的作用，我们对图7中使用的四个测试问题在进化过程中监测每个群体中的解决方案。图8为在探索阶段、切换点和开发阶段解的分布情况。从图8中，我们可以观察到以下情况。
1）在探索阶段，auxPop向无约束PF移动，得到的目标值比mainPop更好，如图8(a) - (d)所示。mainPop喜欢呆在可行的区域。
2）在切换搜索阶段时，auxPop已经到达无约束PF，如图8(e) - (h)所示。另一方面，mainPop的位置取决于每个问题的无约束PF和真PF之间的关系。对于图8(e)中的LIRCMOP6和图8(f)中的CTP7，由于真PF与无约束PF相同或部分重合，mainPop可以在switch point找到真PF。对于图8(g)中的MW7和图8(h)中的LIRCMOP1，真正的PF没有被完全覆盖。

在开发阶段，mainPop遵循可行性规律，继续向真正的PF演进。auxPop也越来越接近真正的PF，如图8(1)所示，auxPop在真正PF上比mainPop覆盖了更广的区域。具体来说，auxPop分布在可行区域和不可行区域。auxPop中的不可行的解决方案位于真正的PF周围，具有良好的客观值和低约束违反。图8(j) - (l)表明，这些非可行解可以补充mainPop，找到所有的真PF。

备注: 在DD-CMOEA中，一方面，mainPop保持了迄今为止发现的所有的良好可行的解。另一方面，auxPop不仅可以引导mainPop在探索阶段通过不可行区域，还可以利用接近真PF的不可行方案，为mainPop在开发阶段提供有用的信息。在auxPop的帮助下，mainPop的收敛性和多样性都得到了增强。

4.2.2 Investigation into the Effect of Using Dual Stages

在这个实例研究中，我们研究了使用双阶段的基本原理，在本案例研究中，将DD-CMOEA与两种单阶段变体(标记为V变体1和V变体2)进行比较。变体1和变体2在其演化过程中分别只使用探索阶段和开发阶段。注意，这三种算法中的所有其他操作都是相同的。为了观察这两个阶段的个体效应，以LIRCMOP1和LIRCMOP9为例，将每个算法在特定的几代上得到的解绘制在图S-6和图S-7中。相应的观察结果如下。
1）变体1的auxPop通过探索搜索，能够充分地通过不可行区域并接近无约束PF。在LIRCMOP9的情况下，它有助于mainPop找到真正的PF，而不会受到不可行的障碍的阻碍。而对于LIRCMOP1，其真PF位于约束边界上时，则auxPop离真正的PF还很远，对mainPop的发展也没什么帮助。
2）在变体2中，auxPop总是能够利用约束边界附近的不可行解。由于利用了这些解，变体2在求解LIRCMOP1时可以得到一个分布良好的解集。但变体2由于探索能力不强，未能通过LIRCMOP9大不可行的区域。
3） DD-CMOEA在这些问题上都获得了很好的解集。由于探索与开发之间的良好平衡，DD-CMOEA不仅能顺利通过不可行区域，而且无论其位置如何，最终都能很好地向真正的PF收敛。
注意： 在两个阶段中，DD-CMOEA使用两种不可行解，一个在无约束PF上，另一个在约束边界上。这两个阶段的使用有助于DD-CMOEA在不同类型的问题上有效地找到真正的PF。

4.2.3 Performance Comparison on Benchmark Problems

在本小节中，将DD-CMOEA在三个测试套件上与五个同行CMOEAs进行比较。我们使用两种广泛使用的度量——反向世代距离(IGD)[33]和hypervolume (HV)[34]——来定量评估它们的性能。由于页面限制，本文仅分析IGD结果，HV结果在补充文件中给出。对IGD和HV结果采用95%置信水平的非参数wilcoxon秩和双边比较检验[35]。它将DD-CMOEA与各竞争对手进行了配对比较。符号’ + '、'−’或’≈’表示对应的竞争对手优于、劣于或可与DD-CMOEA相媲美。此外，每个问题的最佳度量值在每个表中以灰色突出显示。
1） CTP 测试集合：表一显示了DD-CMOEA与五种算法在IGD度量上的比较结果(包括31次运行的平均值和标准差)。这些实证结果证明了DD-CMOEA的竞争力，在表一的所有CTP测试问题上(除了CTP7上的CCMO外)，它都优于所有比较算法。接下来，我们将详细解释这些结果。
CTP7的真实PF是其无约束PF的一部分，并且是断开的。在DD-CMOEA和CCMO中，它们的辅助种群可以找到完全无约束的PF，有助于获得具有良好多样性的真正PF。因此，这两种算法比其他算法表现出更好的性能。对于CTP1，大约三分之一的真实PF来自无约束PF，而另外三分之二来自约束边界。在这种情况下，DD-CMOEA明显优于其他CMOEA。原因是真正的PF的后部分比前部分更难找到，使得大多数算法很难得到整个真正的PF。然而，这个困难可以通过DD-CMOEA克服，因为auxPop中的解决方案从不同的子区域收敛到真正的PF。对于CTP2-CTP5,CMOEAs的可行域边界呈锯齿状，其真正的pf是不连通的(甚至是离散的)，这对CMOEAs保持良好的多样性提出了挑战，如图S-8所示。在这四个问题上，DDCMOEA利用真实前沿上的的不连通区域之间的不可行解获得了最好的结果。此外，在CTP6和CTP8中，一些不可行区域阻碍了对真正PFs的搜索，从而阻碍了部分CMOEAs(如C-NSGA-II和ToRNSGA-II)的收敛进程。从表一可以看出，C-NSGA-II和ToR-NSGA-II在CPT6和CPT8上的IGD结果远差于其他四种CMOEAs。在这些算法中，DD-CMOEA尤其突出，因为它的auxPop算法可以在探索阶段轻松突破不可行的障碍，并在开发阶段围绕真实PF开发不可行的解决方案。

MW测试套件:表二显示了IGD的平均值和方差在算法随机执行31次的结果。如表二所示，DD-CMOEA在13、14、13、5个问题上显著优于C-NSGA-II、PPSMOEA/S、ToR-NSGA-II和CCMO。与C-TAEA相比，DDCMOEA在10个问题和1个问题上分别有较好的和可比较的结果，而C-TAEA在其余3个问题上有较好的结果。

如表二所示，DD-CMOEA在除MW6、MW10、MW13外的几乎所有问题上都比其他算法有更好或等价的性能。DD-CMOEA的竞争力归因于两个种群的互补运作以及探索和开发之间的适当平衡，如第IV- b节所述。MW6、MW10和MW13具有相同的特征，即无约束PF的某些部分构成了真实的PF，而它们附近的可行区相当狭窄。对于提议的DD-CMOEA来说，要找到所有这些狭窄的部分并不容易。C-TAEA能够克服这一挑战，因为它使用面向多样性的档案来增强多样性。虽然与C-TAEA相比，DD-CMOEA在这三个问题上存在不足，但与CCMO相比仍具有可比性，优于其他三家竞争对手。MW10上的实验结果如图S-9所示。
特别值得注意的是，当6个CMOEAs在每个MW问题上进行比较时，总是C-TAEA、CCMO或DD-CMOEA中的一个胜出。其中，DDCMOEA的成功率最高，相对优势最明显。C-TAEA、CCMO和DD-CMOEA的一个共同特征是，它们在进化过程中都使用了两个协作群体(或档案)。然而，DD-CMOEA与C-TAEA和CCMO在勘探开发策略上有所不同。因此，上述结果暗示了保持两个种群的优点，也表明了DD-CMOEA所采用的策略的有效性。
1. LIRCMOP测试套件:我们还使用LIRCMOP测试套件中的14个问题，将DD-CMOEA与其他算法进行比较。从表三可以看出，在所有LIRCMOP问题上，DD-CMOEA都明显优于C-NSGA-II、ToR-NSGA-II和CTAEA。DDCMOEA与PPSMOEA/D在10个、2个和2个问题上的性能分别优于、可比和劣于PPSMOEA/D。与CCMO相比，DD-CMOEA在9个问题上表现更好，在其他5个问题上表现同样好。
在LIRCMOP5、LIRCMOP6和LIRCMOP13的每一种情况下，真实PF和无约束PF是相同的。在这三个问题上，DD-CMOEA要么优于竞争对手，要么具有可比性。对于LIRCMOP9 - LIRCMOP12，真实的pf是断开连接的，并且接近或者不受约束的PF的一部分。如表三所示，虽然PPS-MOEA/D在LIRCMOP9上的表现优于DD-CMOEA，但DD-CMOEA在LIRCMOP10上表现最好，并与CCMO在LIRCMOP11-LIRCMOP12上并列第一。表III中，在LIRCMOP9上DD-CMOEA的平均性能略低于PPS-MOEA/D，这是由于在某些运行中对PF的某些部分搜索不足。然而这种个问题并不是经常发生。尽管PPS-MOEA/D和DD-CMOEA的平均IGD值相差很小(0.00319和0.00354)，但是标准差相差很大(0.000126和0.00420)。在大多数情况下，DD-CMOEA可以找到真正的PF，如图S-10所示。在这四个问题上，DDCMOEA和PPS-MOEA/D算法表现出了相似的性能，并且明显优于其他算法。如图S-11所示，通过DD-CMOEA和PPS-MOEA/D算法得到的最终种群具有比其他算法更好的多样性。原因可能是，从无约束多函数方程中寻找真正的多函数方程有助于在这类问题中找到各种各样的解决方案。对于LIRCMOP7、LIRCMOP8和LIRCMOP14，它们的pf位于约束边界上。DD-CMOEA在LIRCMOP8上表现最好，与CCMO在LIRCMOP7和LIRCMOP14上并列第一，这得益于两个种群的协作。在LIRCMOP14上，DD-CMOEA得到的最终解以及所有比较算法如图S-12所示。

Discussion: 图9总结了六种算法对所有问题(在三个测试套件中)的平均排名，其中使用Friedman测试来检测它们的差异。排序越低，算法的性能越好。注意，wilcoxon秩和检验用于一次只比较两种算法，而Friedman检验用于根据总体性能对所有算法进行排序。在图9中，DD-CMOEA和CCMO分别表现最好和次之。在图9中，这两种算法明显优于其他四种算法。在表四中，我们显示了每个测试套件中每个算法在测试问题上运行的平均计算时间。虽然DD-CMOEA比C-NSGA-II、ToR-NSGA-II和PPSMOEA/D需要更多的计算时间，但比CCMO(图9中排名第二)和C-TAEA要快。从图9和表4可以看出，与目前五种最先进的算法相比，本文提出的DD-CMOEA算法是一种很有前景的算法。

现在我们简要讨论为什么DD-CMOEA在不同的测试套件中获得最佳性能。如IV-B节所示，DD-CMOEA中的两个种群表现出合作。在探索阶段，auxPop是保证能够能够穿过不可行区域而mainPop可以很好地维护可行的解决方案。这样就可以很好地解决第一类问题。此外，在开发阶段，主pop和辅助pop能够协同向真正的PF靠拢。在无约束PF和真实PF相同的情况下，两个群体可以继续合作寻找目标值更好的解;对于两个PF不同的问题，mainPop和auxPop可以分别从可行面和无约束PF向真实PF移动。从实验结果也可以看出，DD-CMOEA的竞争力是由于两个种群的互补运作和探索与开发之间的适当平衡。
但是，当无约束PF和真实PF之间相差距离较远时，DD-CMOEA的搜索效率会降低。例如，多目标背包问题的无约束最优解是选择所有项目:x =(1,1，…， 1).该解具有最大约束冲突。当背包容量较小时，每个Pareto最优解只包含少量的物品。例如，如果背包的容量约为给定物品总重量的10%，那么每个帕累托最优解包含约10%的给定物品。即使在这种情况下，无约束最优解也包括所有给定的项目(即100%的给定项目)。在这种情况下，直观地看，提出的算法似乎不是有效的。

4.2.4 Sensitivity Analysis of Parameter

如Section III-B-3 所说，用于计算变化率的迭代间隔lgap是决定搜索阶段切换时机的一个重要参数。此处设计实验用于验证l_gap参数的设置数值。–从图10中可以看出l_gap值取20是最好的。

6.Conclution

针对约束多目标优化问题(cops)，提出了一种基于双阶段和双种群的算法——DD-CMOEA。DD-CMOEA将进化过程划分为两个种群(即mainPop和auxPop)合作执行的探索和开发阶段。对DD-CMOEA行为的研究表明，两个种群在搜索过程中具有互补性。具体来说，mainPop关注可行性，它可以在整个演进过程中维护可行的解决方案。另一方面，auxPop专注于目标优化。它帮助DD-CMOEA在探索阶段通过不可行的区域，并在开发阶段利用接近真PF的有希望的不可行的解决方案。我们通过在CTP、MW和LIRCMOP测试套件以及一个实际应用问题上，将DDCMOEA与五种最先进的cmoea进行比较，充分证明了DDCMOEA的有效性。实验结果表明，与比较算法相比，DD-CMOEA具有更好的综合性能。DD-CMOEA相对于竞争对手的优势解释如下。(i)在DD-CMOEA中使用两个种群有助于从可行区域和不可行区域对真正的PF进行有效搜索，这通常比单种群算法(即pp - moea /D、ToR-NSGA-II和c - nsgai)更有效。(ii) DD-CMOEA采用了两个搜索阶段，便于在后期有效地搜索可行解，通常比单阶段算法(如C-TAEA、ToR-NSGA-II、CCMO、C-NSGA-II)更有效。(3)两种群间复杂的协作机制以及两个搜索阶段的使用，使得DD-CMOEA算法比其他两种群算法(C-TAEA和CCMO)更有效。
本文的研究开辟了几个有趣的未来方向。(i)在探索和开发之间取得了良好的平衡，大大有利于寻求有竞争力的解决办法。然而，目前还缺乏对搜索阶段切换的理论指导。因此，未来可以在这个方向上进行更多的研究。(ii)在实际应用中，几乎所有的优化问题都具有不同特征的约束。有些问题具有动态约束[36]。其他一些问题也有大量的约束条件[37]。此外，一些约束对[38]的求值非常昂贵。具有这些约束的多目标问题(即具有动态约束、多约束和代价约束的多目标问题)也是未来研究的热点。(iii)在本文中，mainPop和auxPop这两个总体具有预先设定的固定总体规模N(即两目标问题N = 100，三目标问题N = 105)。由于本文对各种测试问题和一个实际问题都取得了良好的实验结果，因此同样的总体大小规格也可用于两个或三个目标的新实际问题。对于有三个以上目标的现实问题，可能需要更多的人口，因为需要更多的解决方案来覆盖整个帕累托阵线。尽管auxPop的种群大小应该与权重向量的数量相同(如MOEA/D中的种群大小规格)，但我们可以任意指定mainPop的种群大小。也就是说，我们可以为每个种群使用不同的种群大小规格。

7. REFERENCES

[1] K. Deb, Multi-Objective Optimization Using Evolutionary Algorithms. Chichester, U.K.: John Wiley & Sons, 2001.

[2] J. Wang, W. Ren, Z. Zhang, H. Huang, and Y . Zhou, “A hybrid multiobjective memetic algorithm for multiobjective periodic vehicle routing problem with time windows,” IEEE Trans. Syst., Man, Cybern., Syst., 2018.

[3] R. Tanabe and A. Oyama, “A note on constrained multi-objective optimization benchmark problems,” in Proc. IEEE Congr . Evol. Comput. (CEC), 2017, pp. 1127–1134.

[4] Z. Ma and Y . Wang, “Evolutionary constrained multiobjective optimization: Test suite construction and performance comparisons,” IEEE Trans. Evol. Comput., vol. 23, no. 6, pp. 972–986, 2019.

[5] K. Deb, A. Pratap, S. Agarwal, and T. Meyarivan, “A fast and elitist multiobjective genetic algorithm: NSGA-II,” IEEE Trans. Evol. Comput., vol. 6, no. 2, pp. 182–197, 2002.

[6] Z. Fan, W. Li, X. Cai, H. Huang, Y . Fang, Y . Y ou, J. Mo, C. Wei, and E. Goodman, “An improved epsilon constraint-handling method in MOEA/D for CMOPs with large infeasible regions,” Soft Comput., pp. 1–20, 2017.

[7] K. Li, R. Chen, G. Fu, and X. Yao, “Two-archive evolutionary algorithm for constrained multiobjective optimization,” IEEE Trans. Evol. Comput., vol. 23, no. 2, pp. 303–315, 2018.

[8] M. Elarbi, S. Bechikh, and L. B. Said, “On the importance of isolated infeasible solutions in the many-objective constrained NSGA-III,” Knowledge-Based Systems, 2018.

[9] Z. Fan, W. Li, X. Cai, H. Li, C. Wei, Q. Zhang, K. Deb, and E. Goodman, “Push and pull search for solving constrained multiobjective optimization problems,” Swarm Evol. Comput., vol. 44, pp. 665–679, 2019.

[10] Z. Ma, Y . Wang, and W. Song, “A new fitness function with two rankings for evolutionary constrained multiobjective optimization,” IEEE Trans. Syst., Man, Cybern., Syst., 2019.

[11] Y . Tian, T. Zhang, J. Xiao, X. Zhang, and Y . Jin, “A coevolutionary framework for constrained multi-objective optimization problems,” IEEE Trans. Evol. Comput., 2020.

[12] C. M. Fonseca and P . J. Fleming, “Multiobjective optimization and multiple constraint handling with evolutionary algorithms – Part I: A unified formulation,” IEEE Trans. Syst., Man, Cybern. A, Syst., Humans, vol. 28, no. 1, pp. 26–37, 1998.

[13] H. Jain and K. Deb, “An evolutionary many-objective optimization algorithm using reference-point based nondominated sorting approach, part II: Handling constraints and extending to an adaptive approach,” IEEE Trans. Evol. Comput., vol. 18, no. 4, pp. 602–622, 2013.

[14] Y . G. Woldesenbet, G. G. Yen, and B. G. Tessema, “Constraint handling in multiobjective evolutionary optimization,” IEEE Trans. Evol. Comput., vol. 13, no. 3, pp. 514–525, 2009.

[15] M. A. Jan and R. A. Khanum, “A study of two penalty-parameterless constraint handling techniques in the framework of MOEA/D,” Appl. Soft Comput., vol. 13, no. 1, pp. 128–148, 2013.

[16] T. Takahama and S. Sakai, “Efficient constrained optimization by the ε constrained adaptive differential evolution,” in Proc. IEEE Congr . Evol. Comput. (CEC), 2010, pp. 1–8.

[17] Y . Wang and Z. Cai, “Combining multiobjective optimization with differential evolution to solve constrained optimization problems,” IEEE Trans. Evol. Comput., vol. 16, no. 1, pp. 117–134, 2012.

[18] E. Mezura-Montes and C. A. C. Coello, “Constraint-handling in natureinspired numerical optimization: past, present and future,” Swarm Evol. Comput., vol. 1, no. 4, pp. 173–194, 2011.

[19] W. Ning, B. Guo, Y . Yan, X. Wu, J. Wu, and D. Zhao, “Constrained multi-objective optimization using constrained non-dominated sorting combined with an improved hybrid multi-objective evolutionary algorithm,” Eng. Optim., vol. 49, no. 10, pp. 1645–1664, 2017.

[20] Q. Zhang and H. Li, “MOEA/D: A multiobjective evolutionary algorithm based on decomposition,” IEEE Trans. Evol. Comput., vol. 11, no. 6, pp. 712–731, 2007.

[21] Z. Liu and Y . Wang, “Handling constrained multiobjective optimization problems with constraints in both the decision and objective spaces,” IEEE Trans. Evol. Comput., vol. 23, no. 5, pp. 870–884, 2019.

[22] K. Li, K. Deb, Q. Zhang, and S. Kwong, “An evolutionary manyobjective optimization algorithm based on dominance and decomposition,” IEEE Trans. Evol. Comput., vol. 19, no. 5, pp. 694–716, 2015.

[23] X. Li and X. Yao, “Cooperatively coevolving particle swarms for large scale optimization,” IEEE Trans. Evol. Comput., vol. 16, no. 2, pp. 210– 224, 2011.

[24] J. Wang, G. Liang, and J. Zhang, “Cooperative differential evolution framework for constrained multiobjective optimization,” IEEE Trans. Cybern., vol. 49, no. 6, pp. 2060–2072, 2018.

[25] J. Wang, W. Zhang, and J. Zhang, “Cooperative differential evolution with multiple populations for multiobjective optimization,” IEEE Trans. Cybern., vol. 46, no. 12, pp. 2848–2861, 2015.

[26] H.-L. Liu, F. Gu, and Q. Zhang, “Decomposition of a multiobjective optimization problem into a number of simple multiobjective subproblems,” IEEE Trans. Evol. Comput., vol. 18, no. 3, pp. 450–455, 2013.

[27] E. Zitzler, M. Laumanns, and L. Thiele, “SPEA2: Improving the strength Pareto evolutionary algorithm,” TIK-report, vol. 103, 2001.

[28] K. Deb, R. B. Agrawal et al., “Simulated binary crossover for continuous search space,” Complex Syst., vol. 9, no. 2, pp. 115–148, 1995.

[29] K. Deb and M. Goyal, “A combined genetic adaptive search (GeneAS) for engineering design,” Comput. Sci. Inform., vol. 26, pp. 30–45, 1996.

[30] K. Deb, A. Pratap, and T. Meyarivan, “Constrained test problems for multi-objective evolutionary optimization,” in Proc. Int. Conf. Evol. Multi Criterion Optim. (EMO). Springer, 2001, pp. 284–298.

[31] K. Price, R. M. Storn, and J. A. Lampinen, Differential evolution: A practical approach to global optimization. Springer Science & Business Media, 2006.

[32] Y . Tian, R. Cheng, X. Zhang, and Y . Jin, “PlatEMO: A MA TLAB platform for evolutionary multi-objective optimization,” IEEE Comput. Intell. Mag., vol. 12, no. 4, pp. 73–87, 2017.

[33] P . A. Bosman and D. Thierens, “The balance between proximity and diversity in multiobjective evolutionary algorithms,” IEEE Trans. Evol. Comput., vol. 7, no. 2, pp. 174–188, 2003.

[34] E. Zitzler and L. Thiele, “Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach,” IEEE Trans. Evol. Comput., vol. 3, no. 4, pp. 257–271, 1999.

[35] M. Hollander, D. A. Wolfe, and E. Chicken, Nonparametric statistical methods. John Wiley & Sons, 2013, vol. 751.

[36] R. Azzouz, S. Bechikh, and L. Ben Said, “Multi-objective optimization with dynamic constraints and objectives: New challenges for evolutionary algorithms,” in Proc. Genetic Evol. Comput. Conf. (GECCO), 2015, pp. 615–622.

[37] M. Ming, R. Wang, and T. Zhang, “Evolutionary many-constraint optimization: An exploratory analysis,” in Proc. Int. Conf. Evol. Multi Criterion Optim. (EMO). Springer, 2019, pp. 165–176.

[38] K. H. Rahi, H. K. Singh, and T. Ray, “Partial evaluation strategies for expensive evolutionary constrained optimization,” IEEE Trans. Evol. Comput., 2021.