MFO问题与MFEA算法
- MFO问题的思想
- MFEA算法
- MFEA的启示
- MFEA在连续问题上的优化能力
- MFEA在离散问题上的讨论
- MFEA在具有离散问题的任务集上的优化能力
- 1.多任务同时开始时的情况
- 2.多任务不同时开始时的情况
声明:此博文是论文Multifactorial Evolution: Towards Evolutionary Multitasking的简要中文概述,概括与翻译仅为学习。如有侵权请联系本人删除博文。
MFO问题的思想
多目标优化(MOO)与单目标优化(SOO)是我们常用的优化方法,然而二者的效率却存在瓶颈。另外,现有的优化算法往往忽视了不同任务之间相互协作的能力。多任务优化思想(MFO)就是借助任务之间隐含的并行性,对多个任务同时优化,在完成优化任务的同时提高优化效率。在MFO问题中,同时进行的多个任务的依赖性是提前不可预知的,且任务之间的搜索空间可以相同也可以不同。另外,MFO支持连续与离散的任务同时处理。
为了进一步说明MFO问题,假设一个多任务优化问题有K个任务,每个任务都是单目标的最小化问题。 其中第j个问题计为Tj,该问题自变量搜索空间(search space)记为Xj,对应的函数是 fj : Xj→ ℝ。多任务优化的目的就是对于所有任务,寻找到在任务搜索空间上的一组值{x1, x2, ….,xK-1, xK},使其满足{x1, x2, ….,xK-1, xK}= argmin {f1(x), f2(x), …., fK-1(x), fK(x)}。
MFEA算法
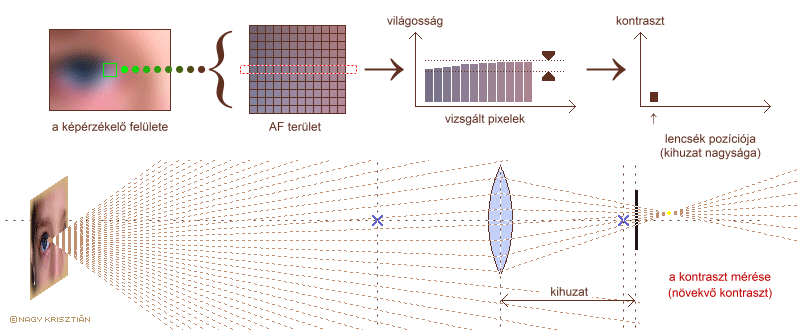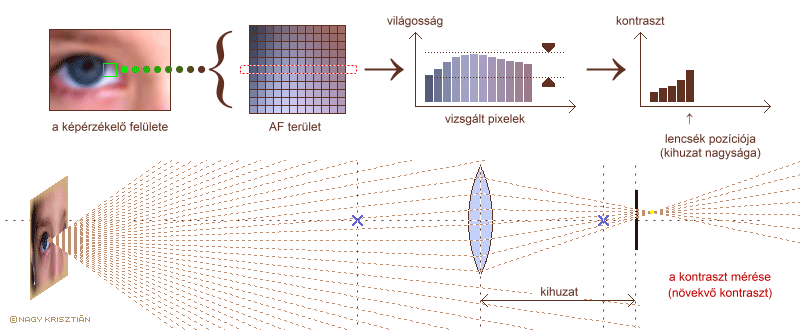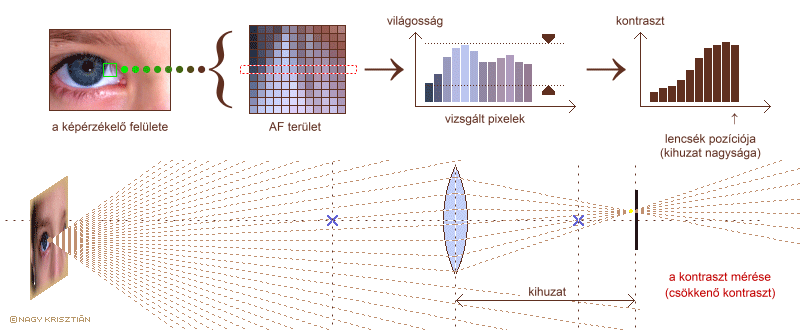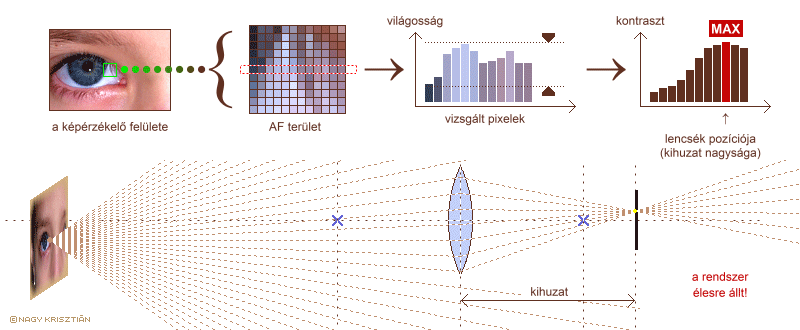
MFEA算法的提出便是为了解决MFO问题。MFEA基于遗传算法与文化基因算法。受文化基因算法的影响,MFEA认为对某种任务具有优势地位的个体(具有相同技能因子的个体)之间更容易产生后代。以下五个定义将被运用于实际的编码过程:
Definition 1 (Factorial Cost):对于个体pi的任务Tj,有factorial cost :𝛹ji=𝜆 ∙ 𝛿𝑗𝑖 +𝑓𝑗i 其中𝜆是惩罚因子,𝛿是违反约束总数,f为目标函数值
Definition 2 (Factorial Rank): 对于个体pi的任务Tj,factorial rank: rji 是指个体i在j任务上依据 factorial cost 的排名。当出现排名相同的情况时采用 random tie-breaking解决。同时将这两个个体称为j-counterparts。
Definition 3 (Scalar Fitness):对于个体pi的所有任务,均有其对应的factorial rank。取所有任务中factorial rank的最小值进行倒数运算的结果为scalar fitness,即φi = 1/ min𝑗∈{1,…,𝐾}{𝑟𝑗𝑖}.
Definition 4 (Skill Factor):对于个体pi,在所有任务中选取它表现最好的一个任务Tj,记为:τi =𝑎𝑟𝑔𝑚𝑖𝑛𝑗{𝑟𝑗𝑖} where j ∈ {1, 2, …, K}。当两个个体的factorial rank与skill factor均相同时,称之为 strong counterparts。
Definition 5 (Multifactorial Optimality):对应个体 p*,仅当它在所有任务表现均为最优时才称之为多因素最优。
对于连续问题的MFEA算法结构如下所示:
1.随机产生N个个体,并生成初始种群P0//其中每个个体的染色体的维度与所有任务中最大维度的任务的维度相同。
2.for 初始种群的每个任务 do
3. 对所有个体在该任务上通过拟牛顿法进行预学习//可选其他预学习方法
4. 更新染色体信息
5. 计算所有个体在该任务上的Factorial Cost
6. end for
7 .计算初始种群的factorial rank,scalar fitness,skill factor。
8.t=0
9.while(终止条件不满足) do
10. 将初代种群随机配对
11. 生成0-1间的随机数rand
12. if(父skill factor=母skill factor)or(rand<rmp) then//rmp是预先定义好的随机交配概率
13. 父母之间进行交叉操作得到两个子代//二进制交叉
14. 生成0-1间的随机数rand1
15. if(rand1<0.5)then
16. 子代1继承父代1的skill factor
17. else
18. 子代1继承父代2的skill factor
19. 生成0-1间的随机数rand2
20. end if
21. if(rand2<0.5)then
22. 子代2继承父代1的skill factor
23. else
24. 子代1继承父代2的skill factor
25. end if
26. else
27. 两个父代进行变异,分别得到两个子代//高斯变异产生子代
28. 子代分别继承父代的skill factor
29. end if
30. for 子代种群的每个任务 do
31. 对技能因子符合该任务上的个体通过拟牛顿法进行预学习//可选其他预学习方法
32. 更新染色体信息
33. 计算目标个体在该任务上的Factorial Cost
34. end for
35. 将子代种群与父代种群合并
36. 计算合并后种群的factorial rank,scalar fitness,skill factor。
37. 利用roulette wheel法对合并后的种群进行选择,生成下一代种群。
38. t=t+1
39.end whileMFEA的启示
MFEA根据skill factor的不同将种群分为不同的技能组。然而,不同组的遗传物质也有可能对另一组产生作用。通过设置好的rmp概率与子代对父母技能的模仿实现不同技能组之间的通信,从而使遗传物质在不同技能组之间转移。相互沟通的遗传物质是实现算法隐含并行性的关键原因。
另外,MFEA仅对个体表现较好的任务进行评估,这在很大程度上减少了计算的复杂度,使算法同时处理多个复杂任务变为可能。
MFEA在连续问题上的优化能力
使用以下无约束基准函数进行测试:

MA与MR是随机生成的旋转矩阵,OA与OR是相关函数的全局最优解。其中Sphere函数相对简单,而Rastrigin函数相对复杂。
1.首先考虑全局最优值相交的情况。
设置OA=OR=0(原点处),且将函数的搜索空间均定为[-50,50],以确保确实存在有用的遗传物质,且遗传物质可以在不同任务中相互转移。将函数变量维度定为20维或30维,且为了书写方便,任务表示为维数+函数首字母。如20S或30A。在多任务处理过程中,同时处理的一组任务用小括号集中一起,如(20S,20A)。设置两个问题集合:
F1:{(30R, none), (30R, 30S), (30R, 30A), (30R,20S)}
F2:{(30A, none}, (30A, 30S), (30A, 30R), (30A, 20S), (30A,20R)}
设置种群包含100个个体,且迭代500次。设置rmp=0.3,父母生成子代的方法采用二进制交叉与高斯变异。对函数的预学习采用拟牛顿法。对问题集合F1与F2产生结果如下图所示:

由图a可以看到,当Rastrigin函数与其他函数一起
处理时,其收敛率得到了显著的提高。对图b进行观察后可得知 Ackley函数与Rastrigin函数均在多任务处理过程中得到了优化,二者协同运作绕过了障碍,使函数快速收敛。
2.接下来考虑跨函数进行处理的案例
对于(30R,30A)的任务,在设置OR=0的同时,设置OA偏移的三种情况:
a.偏移量为0-2(SS)
b.偏移量为2-5(MS)
c.偏移量为5-10(LS)
此外,如下图所示,将 Ackley 函数变量的搜索空间范围设置为 [-32, 32],Rastrigin 的函数变量的范围设置为 [-5, 5]以实现搜索空间异构。在此时可以发现,在LS情况下,Ackley 函数的最佳值位于 Rastrigin 函数变量的边界之外。

将上述任务利用MFEA算法进行计算,基本参数沿袭情况1,可得结果如下

由此可见,即使不同任务之间没有明显的遗传互补性来源,从受控跨文化交配中产生的探索也有助于优化。
MFEA在离散问题上的讨论
在MFEA中,不同任务在每个个体的染色体上编码形式是统一的。处理连续问题仅需简单的归一化处理就可以将信息编码入染色体。然而对于离散问题来说,需要进行特殊的处理以便形成一个统一的解码器。通常,组合问题可以通过有限接地状态 S = {1、2、3、…、n}定义,从而产生一个离散搜索空间,该空间由一组可行的解决方案 X = 2S 组成,其中每个解决方案映射到实际函数值,如 f : 2S= R 。这种看似简单的描述会导致各种各样的问题。因此,为后续演示选择了以下众所周知的组合优化问题:a) 0/1 单卡背包问题,b) 二次分配问题,c) 有能力约束的车辆路径调度问题。
1.KP与MKP(背包问题)
在MKP问题中定义m个背包,每个背包容量为W1,W2,……Wm,有n个物品,第i个物品在第k个背包中的重量是wik,物品对应的价值记为qi。一个物品要么放入所有背包,要么一个都不放入。
在MFEA中,生成一个随机键向量(y1、y2、…,yn)代表一组基因,这n个基因值可以在0-1上自由移动,这些基因值可以通过实数编码的运算器进行处理,每个基因都代表了一个物品。并用Single-linkage聚类法将物品分为两类,最后舍弃一类保留另一类。若所选群集中项目的总重量违反了背包的容量限制。则使用 Dantzig 的贪婪近似算法 ,按项目利润与权重比排序删除多余任务。
2.QAP(二次分配问题)
QAP问题目的是将n个设施分配给n个地点,每个地点对应一个设施。目的是使一个二次目标函数得到优化。
在这个问题中,一个个体第i个随机键记为第i个设施的标签,分配设施只需将随机键进行升序排序并根据设施在排序表中的位置分配。例如,让我们考虑一组标记为 {1、2、3}的位置和一组由随机键表示的 3 个设施:(0.7、0.1、0.3)。根据规定的分配技术,设施 2 分配给位置 1,设施 3 分配给位置 2,设施 1 分配给位置 3。
在该情况中,采用 2-exchange heuristic 对候选的分配方案进行改进。
3.CVRP(有能力约束的车辆路径调度问题)
可将CVRP问题在图上展现,将图上的一个节点表示为一个车辆仓库,其余节点标识有需求的客户。CVRP的目的使寻找一个路线安排,在仅为每个客户服务一次的情况下使路线最短。其中不同客户在要求的时间段获得服务会让他们更加满意。
在这个问题中,使用第 i 个随机键来标记第 i 号客户。此后,只需按升序对随机键进行排序(如 QAP 的情况),即可推断出 TSP线路。接下来,将TSP 路线划分为单独的车辆行程,最终获得高质量的解决方案。
为了更好的展示离散问题与连续问题的处理,设计一个跨领域的多任务处理过程。包含三个任务
a) 有五个变量的连续问题,每个变量在范围 [0,5] 范围内,b) 包含 10 个项目的 KP,c) 具有 10 个设施点(和 10 个位置)的 QAP。在此任务中,染色体维数D取三个任务维数的最大值10.生成一个随机的染色体:: (0.79, 0.31, 0.53, 0.17, 0.60, 0.26, 0.65, 0.69,0.75, 0.45)。
1.对于连续问题,仅需将染色体前五维从0-1的空间映射在0-5的空间即可完成解码。
2.对于背包问题,将染色体中的值放置于实数线上,利用single-linkage聚类方法分为两类,将不合背包容量的一类淘汰,剩下的一类即可解码为需要的表现形式。
3.对于QAP问题,将生成的染色体中的值映射在实数线上即可直接解码,为 (4, 6, 2, 10,3, 5, 7, 8, 9, 1)。

图片总结了上述的描述过程
MFEA在具有离散问题的任务集上的优化能力
1.多任务同时开始时的情况
设置了四个问题集,从广义上讲,这些问题集可以分为三类。Set 1 由排序问题(即 QAP 和 CVRP)组成,在解码时必须对随机键进行排序。Set 2 中的任务与此类似,它们各自的随机键解码过程要求对基因进行二进制聚类。集 3 和 4 是跨域多任务处理的实例,合并了排序、二进制聚类和连续优化三种问题。此处报告了 MFEA 对上述问题集的结果。(详情见下表)

对于KP问题,设置wi为1-10内的随机数,qi=wi+5。背包容量取所有物品重量的平均值。对于MKP问题𝑤𝑖𝑘 = uniformly random [1, 10] , 𝑞𝑖 = 𝑚𝑒𝑎𝑛𝑘(𝑤𝑖𝑘)+5.,第k个背包容量取对该背包而言所有物体重量的平均值。
MFO 和 SOO 运用相同的染色体表示方案。在连续优化问题中采取SBX(二进制交叉)和高斯突变作为交叉与突变方法。在 MFEA 中,rmp 设置为 0.3。为了进行对比,取一个任务运行期间的最小值𝑓𝑗𝑚𝑖n与最大值 𝑓𝑗𝑚𝑎x,令𝑓̃ja= (𝑓𝑗 − 𝑓𝑗𝑚𝑖n) (𝑓𝑗𝑚𝑎x − 𝑓𝑗𝑚𝑖n)。每个任务运算完成后取 𝑓̃a = (𝑓̃1a +𝑓̃2a+ 𝑓̃3a)/3。四个问题集的运行过程如图:




可以看出,在任何问题集中,多任务算法所得的结果均优于单任务优化算法。下图可以更明显的看出MFEA对每个任务的优化贡献。


其中标注*是指在多任务处理中该任务的收敛情况了。如MFO(T1**,T2,T3)所表示的是在该任务中T1的收敛情况。可以看到,除了set4中的任务T1,MFO中每个任务都得到了加速,且连续优化问题受益明显。这一观察得出的结论是,进化多任务处理不一定保证每个任务的性能提高,因为并非所有的基因转移都很有用。然而在MFO的许多跨域优化问题中,正转移远远大于负转移。
2.多任务不同时开始时的情况
在Solomon’s benchmark set中选取三个时间窗口受限的CVRP实例(c101、c102和c103)。在启动c101后的中间阶段将实例c102(或 c103)呈现给解算器。结果表明,与SOO相比,MFO为c102与c103的搜索过程提供了巨大推动力。


连续问题优化的matlab与python代码链接如下:
[1]: matlab版本
[2]: python版本