- 原理
KNN算法就是在其表征空间中,求K个最邻近的点。根据已知的这几个点对其进行分类。如果其特征参数只有一个,那么就是一维空间。如果其特征参数只有两个,那么就是二维空间。如果其特征参数只有三个,那么就是三维空间。如果其特征参数大于三个,那么就是N维抽象空间。在表征空间中,不同点的距离采用如下所示的欧几里得方法进行计算。
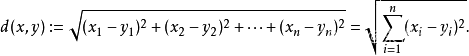
K值根据经验选择最合适的参数,太小不够稳健,太大的话容易受样本不足制约。也可以根据交叉验证的方法,确定最优的K值。一般取5~10之间的一个数。
如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别,则该样本也属于这个类别。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。 看下面这幅图:

KNN的算法过程是是这样的: 从上图中我们可以看到,图中的数据集是良好的数据,即都打好了label,一类是蓝色的正方形,一类是红色的三角形,那个绿色的圆形是我们待分类的数据。 如果K=3,那么离绿色点最近的有2个红色三角形和1个蓝色的正方形,这3个点投票,于是绿色的这个待分类点属于红色的三角形 如果K=5,那么离绿色点最近的有2个红色三角形和3个蓝色的正方形,这5个点投票,于是绿色的这个待分类点属于蓝色的正方形 我们可以看到,KNN本质是基于一种数据统计的方法!其实很多机器学习算法也是基于数据统计的。 KNN是一种memory-based learning,也叫instance-based learning,属于lazy learning。即它没有明显的前期训练过程,而是程序开始运行时,把数据集加载到内存后,不需要进行训练,就可以开始分类了。 具体是每次来一个未知的样本点,就在附近找K个最近的点进行投票。
- 三个距离算法
欧氏距离:是一个通常采用的距离定义,指在n维空间中两个点之间的真实距离,或者向量的自然长度(即该点到原点的距离),在二维和n维空间中的欧氏距离就是两点之间的实际距离。
def euclideanDistance(x1, x2):
# 欧氏距离
tempDistance = 0
for i in range(x1.shape[0]):
difference = x1[i] - x2[i]
tempDistance += difference * difference
tempDistance = tempDistance ** 0.5
return tempDistance
马氏距离:马氏距离(Mahalanobis Distance)是一种距离的度量,可以看作是欧氏距离的一种修正,修正了欧式距离中各个维度尺度不一致且相关的问题。其中Σ是多维随机变量的协方差矩阵,μ为样本均值,如果协方差矩阵是单位向量,也就是各维度独立同分布,马氏距离就变成了欧氏距离。

def mashi_distance(x,y):
X = numpy.vstack([x, y])
XT = X.T
# 方法一:根据公式求解
S = numpy.cov(X) # 两个维度之间协方差矩阵
SI = numpy.linalg.inv(S) # 协方差矩阵的逆矩阵
# 马氏距离计算两个样本之间的距离
n = XT.shape[0]
d1 = 0
for i in range(0, n):
for j in range(i + 1, n):
delta = XT[i] - XT[j]
d = numpy.sqrt(numpy.dot(numpy.dot(delta, SI), delta.T))
d1 = d1 + d
return d1
曼哈顿距离:种使用在几何度量空间的几何学用语,用以标明两个点在标准坐标系上的绝对轴距总和。
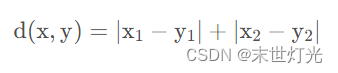
def ManhattanDistance(x, y):
x = numpy.array(x)
y = numpy.array(y)
return numpy.sum(numpy.abs(x-y))
- 三个数据集
Iris数据集:Iris Data Set(鸢尾属植物数据集)是我现在接触到的历史最悠久的数据集,它首次出现在著名的英国统计学家和生物学家Ronald Fisher 1936年的论文《The use of multiple measurements in taxonomic problems》中,被用来介绍线性判别式分析。在这个数据集中,包括了三类不同的鸢尾属植物:Iris Setosa,Iris Versicolour,Iris Virginica。每类收集了50个样本,因此这个数据集一共包含了150个样本。
该数据集测量了所有150个样本的4个特征,分别是:sepal length(花萼长度);sepal width(花萼宽度);petal length(花瓣长度);petal width(花瓣宽度)以上四个特征的单位都是厘米(cm)。通常使用mm表示样本量的大小,nn表示每个样本所具有的特征数。因此在该数据集中,m=150,n=4m=150,n=4。
# iris数据集
tempDataset = sklearn.datasets.load_iris()
葡萄酒分类数据集:Wine葡萄酒数据集是来自UCI上面的公开数据集,这些数据是对意大利同一地区种植的葡萄酒进行化学分析的结果,这些葡萄酒来自三个不同的品种。该分析确定了三种葡萄酒中每种葡萄酒中含有的13种成分的数量。从UCI数据库中得到的这个wine数据记录的是在意大利某一地区同一区域上三种不同品种的葡萄酒的化学成分分析。数据里含有178个样本分别属于三个类别,这些类别已经给出。每个样本含有13个特征分量(化学成分),分析确定了13种成分的数量,然后对其余葡萄酒进行分析发现该葡萄酒的分类。
在wine数据集中,这些数据包括了三种酒中13种不同成分的数量。文件中,每行代表一种酒的样本,共有178个样本;一共有14列,其中,第一个属性是类标识符,分别是1/2/3来表示,代表葡萄酒的三个分类。后面的13列为每个样本的对应属性的样本值。剩余的13个属性是,酒精、苹果酸、灰、灰分的碱度、镁、总酚、黄酮类化合物、非黄烷类酚类、原花色素、颜色强度、色调、稀释葡萄酒的OD280/OD315、脯氨酸。其中第1类有59个样本,第2类有71个样本,第3类有48个样本。
# 葡萄酒分类数据集
tempDataset = sklearn.datasets.load_wine()
手写分类数据集:在这个数据集中,包含1797张8*8灰度的图像。每个数据点都是一个数字,共有10种类别(数字0~9)。
# 手写数字分类数据集
tempDataset = sklearn.datasets.load_digits()
- 实验对比

- 结论
本次实验内容包括三种数据集分别对三种距离测量算法进行knn预测分类,同一种数据集在不同距离测量算法下计算精度也不尽相同。其中,手写数字数据集在使用马氏距离过程中计算量过大,不适宜使用马氏距离计算。
import sklearn.datasets, sklearn.neighbors, sklearn.model_selection
import numpy
from sklearn import metricsdef sklearnKnnTest():#Step 1. Load the dataset# iris数据集#tempDataset = sklearn.datasets.load_iris()# 葡萄酒分类数据集#tempDataset = sklearn.datasets.load_wine()# 手写数字分类数据集tempDataset = sklearn.datasets.load_digits()x = tempDataset.datay = tempDataset.target#print("x = ", x)#print("y = ", y)#Step 2. Split the dataX1, X2, Y1, Y2 = sklearn.model_selection.train_test_split(x, y, test_size = 0.2)print("X1 = ", X1)print("Y1 = ", Y1)print("X2 = ", X2)print("Y2 = ", Y2)#Step 3. Indicate the training set.tempClassifier = sklearn.neighbors.KNeighborsClassifier(n_neighbors = 5)tempClassifier.fit(X1, Y1)#Step 4. Test.tempScore = tempClassifier.score(X2, Y2)print("The score is: ", tempScore)def euclideanDistance(x1, x2):# 欧氏距离tempDistance = 0for i in range(x1.shape[0]):difference = x1[i] - x2[i]tempDistance += difference * differencetempDistance = tempDistance ** 0.5return tempDistance
# 马氏距离
def mashi_distance(x,y):X = numpy.vstack([x, y])XT = X.T# 方法一:根据公式求解S = numpy.cov(X) # 两个维度之间协方差矩阵SI = numpy.linalg.inv(S) # 协方差矩阵的逆矩阵# 马氏距离计算两个样本之间的距离n = XT.shape[0]d1 = 0for i in range(0, n):for j in range(i + 1, n):delta = XT[i] - XT[j]d = numpy.sqrt(numpy.dot(numpy.dot(delta, SI), delta.T))d1 = d1 + dreturn d1
# 曼哈顿距离
def ManhattanDistance(x, y):x = numpy.array(x)y = numpy.array(y)return numpy.sum(numpy.abs(x-y))def mfKnnTest(k = 3):#Step 1. Load the dataset# iris数据集#tempDataset = sklearn.datasets.load_iris()# 葡萄酒分类数据集#tempDataset = sklearn.datasets.load_wine()# 手写数字分类数据集tempDataset = sklearn.datasets.load_digits()x = tempDataset.datay = tempDataset.target#print("x = ", x)#print("y = ", y)#Step 2. Split the dataX1, X2, Y1, Y2 = sklearn.model_selection.train_test_split(x, y, test_size = 0.2)# print("X1 = ", X1)# print("Y1 = ", Y1)# print("X2 = ", X2)# print("Y2 = ", Y2)#Step 3. ClassifytempPredicts = numpy.zeros(Y2.shape[0])for i in range(X2.shape[0]):#Step 3.1 Find k neigbhors#InitializetempNeighbors = numpy.zeros(k + 2)tempDistances = numpy.zeros(k + 2)for j in range(k + 2):tempDistances[j] = 1000tempDistances[0] = -1for j in range(X1.shape[0]):# 欧氏距离#tempDistance = euclideanDistance(X2[i], X1[j])# 马氏距离tempDistance = mashi_distance(X2[i], X1[j])# 曼哈顿距离#tempDistance = ManhattanDistance(X2[i], X1[j])tempIndex = kwhile True:if tempDistance < tempDistances[tempIndex]:#Move forward#print("tempDistance = {} and tempDistances[{}] = {}".format(tempDistance, tempIndex, tempDistances[tempIndex]))tempNeighbors[tempIndex + 1] = tempNeighbors[tempIndex]tempDistances[tempIndex + 1] = tempDistances[tempIndex]tempIndex -= 1else:#Insert heretempNeighbors[tempIndex + 1] = jtempDistances[tempIndex + 1] = tempDistance#print("Insert to {}.".format(tempIndex))break#print("Classifying ", X2[i])#print("tempNeighbors = ", tempNeighbors)#Step 3.2 Vote#Step 2.2 Vote for the classtempLabels = []for j in range(k):tempIndex = int(tempNeighbors[j + 1])tempLabels.append(int(Y1[tempIndex]))tempCounts = []for label in tempLabels:#print("count = ", tempLabels.count(label))tempCounts.append(int(tempLabels.count(label)))tempPredicts[i] = tempLabels[numpy.argmax(tempCounts)]print("The predictions are: ", tempPredicts)print("The true labels are: ", Y2)print('The accuracy of the KNN is: {:.3f}'.format(metrics.accuracy_score(tempPredicts, Y2)))return metrics.accuracy_score(tempPredicts, Y2)def main():#sklearnKnnTest()#print("Life is short, so I study python.")list = []for i in range(6):list.append(mfKnnTest())print(list)main()