二分查找的算法思想
二分查找也称“折半查找”,要求查找表为采用顺序存储结构的有序表。本例一律采用升序排列。二分查找每一次都会比较给定值与序列[low,high]的中间元素,该元素的下标为mid = (low+high)/2,若两者相等,则返回元素的下标为mid;如果arr[mid]>key,说明给定值key在中间元素的左边,此时只需要查找序列[low,mid-1]的中间元素;如果arr[mid]<key,说明给定值key在中间元素的右边,此时只需要查找序列[mid+1,high]。由于每一次比较arr[mid]与key失败都只需要查找剩下序列的一半,故谓之'二分查找'。显而易见,二分查找适合使用递归实现,递归的终止条件为low>high。
代码实现
注意了哈,此处的查找下标从1开始,下标0已经被弃用。
#include<iostream>
using namespace std;int arr[10] = { 0,1,3,5,12,32,42,53,56,89};
//非递归实现
int Search_Bin(const int key) {//最左边的下标从1开始int low = 1, high = 10;while (low <= high) {int mid = (low + high) / 2;if (arr[mid] == key) {return mid;}else if (arr[mid] < key) {low = mid + 1;}else {high = mid - 1;}}return -1;
}//递归实现
int Search_Bin(const int key, int low, int high) {if (low > high) {return -1;}int mid = (low + high) / 2;if (arr[mid] == key) return mid;else if (arr[mid] > key) return Search_Bin(key, low, mid - 1);else return Search_Bin(key, mid+1, high);
}void test01() {cout << "----调用非递归函数------" << endl;cout << "ret = 1的下标为" << Search_Bin(1) << endl;cout << "ret = 43的下标为" << Search_Bin(43) << endl;cout << "ret = 100的下标为" << Search_Bin(100) << endl;cout << "----调用递归函数---------" << endl;int len = sizeof(arr) / sizeof(int);cout << "ret = 1的下标为" << Search_Bin(1,1,len) << endl;cout << "ret = 43的下标为" << Search_Bin(43, 1, len) << endl;cout << "ret = 100的下标为" << Search_Bin(100, 1, len) << endl;
}int main() {test01();return 0;
}
二分查找的判定树
二分查找的过程可以用一棵二叉树来描述,若用二叉树构造序列[low,high]的判定树,那么二叉树的根结点的存储值为序列[low,high]的中间元素的位置mid,而二叉树的左子树构造序列[low,mid-1]的判定树,右子树构造序列[mid+1,high]的判定树。查找给定值key的过程,就是逐一自上而下遍历二叉树根结点的过程。
查找次数不会超过二叉树的深度,假设序列有n个元素,那么查找的次数:count<=[log(2)n]+1。以下构造序列[1,10]的判定树,如图所示,查找的第一个下标必定为5,如果key值较arr[5]小,那么第二个查找的下标必定为2,否则为8。总而言之,倘若查找成功,查找下标的顺序就是二叉树的遍历顺序。

由于判定树的出现只是为了研究二分查找的过程,所以没有代码实现,以下借助判定树分析二分查找的时间复杂度。假设满二叉树的结点为n,j为二叉树的层次,则该层共有2^j-1个结点,由于当查找到第j层的结点时,查找也已与给定值key比较了j次。假设每一个结点被查找到的概率相同,那么每一个结点的平均查找次数为:
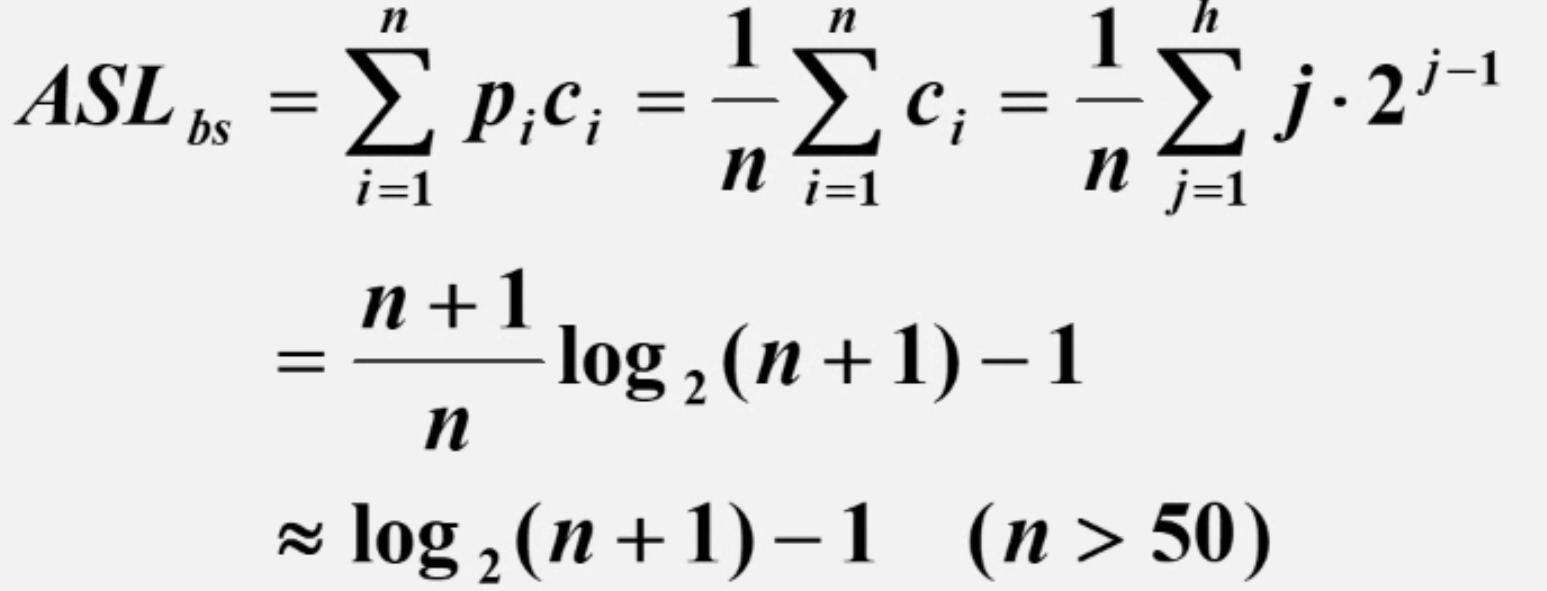
可见当n较大时,时间复杂度为log(2)n,相比于顺序查找提升了很多。
优缺点分析
优点:查找速度快;
缺点:
1.只适用于顺序存储结构的有序表;
2.修改与删除操作会破坏查找表的有序性,因而二分查找适合于静态查找表;
反思
二分查找的要求是,查找表为采用顺序存储结构的有序表,但现实中的有序性不只是体现在数字的比较上。有很多的排序标准是人为规定的,比如字典序,ABCD.......Z人为规定为升序排列;一个国家中的各个省市,可以根据经纬度的高低排序,或根据GDP产出排序.......总而言之,倘若一个问题适合采用二分查找,前提是适合指定解决该问题的排序规则,从而方便查找的实现。
另外,现实中的查找并不只是限制于一个值,还可以是一个范围,比如老师查找某个成绩段之间的所有学生,公司根据员工的绩效分段给员工发不同的奖金,学校要求科目成绩在[90,100]分段就可以给出A绩点等等......
以上就是我对查找学习的一些反思。