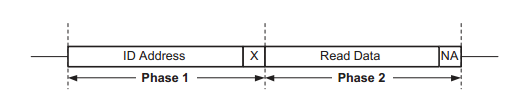
长春网络赛的题。

用的暴力。

XB看了题目，然后直接说他的思路，我俩讨论后敲的，我也没怎么看题。

我的做法是，先将额外的那个点（第一行输入M点），与每个hero为半径的圆求交点，若交点到各个hero的距离小于等于d，则最短是M到交点

所有hero的点以d为半径的圆求交，所交区域如果放上路由器一定能覆盖到所有的hero，所以变成M到这个区域的点的最短距离。

由于第一步的操作，所以M到点的最小距离的那个点一定是在相交圆弧的交点上，所以枚举交点，找最短距离。。。

复杂度N^3，太暴力了。

#include <set>
#include <queue>
#include <stack>
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#include <iostream>
#include <limits.h>
#include <string.h>
#include <string>
#include <algorithm>
#define MID(x,y) ( ( x + y ) >> 1 )
#define L(x) ( x << 1 )
#define R(x) ( x << 1 | 1 )
#define FOR(i,s,t) for(int i=(s); i<(t); i++)
#define BUG puts("here!!!")
#define STOP system("pause")
#define file_r(x) freopen(x, "r", stdin)
#define file_w(x) freopen(x, "w", stdout)using namespace std;const int MAX = 1010;
const double eps = 1e-8;
const double INF = 1e30;
double d;
struct point{double x, y;void get(){scanf("%lf%lf", &x, &y);}
};
point M;
bool dy(double x,double y)	{	return x > y + eps;}	// x > y 
bool xy(double x,double y)	{	return x < y - eps;}	// x < y 
bool dyd(double x,double y)	{ 	return x > y - eps;}	// x >= y 
bool xyd(double x,double y)	{	return x < y + eps;} 	// x <= y 
bool dd(double x,double y) 	{	return fabs( x - y ) < eps;}  // x == y
double disp2p(point a,point b) //  a b 两点之间的距离 
{return sqrt( ( a.x - b.x ) * ( a.x - b.x ) + ( a.y - b.y ) * ( a.y - b.y ) );
}
bool operator==(point a, point b)
{return dd(a.x, b.x) && dd(a.y, b.y);
}
point c[MAX];point l2l_inst_p(point u1,point u2,point v1,point v2)
{point ans = u1;double t = ((u1.x - v1.x)*(v1.y - v2.y) - (u1.y - v1.y)*(v1.x - v2.x))/((u1.x - u2.x)*(v1.y - v2.y) - (u1.y - u2.y)*(v1.x - v2.x));ans.x += (u2.x - u1.x)*t;ans.y += (u2.y - u1.y)*t;return ans;
}
void l2c_inst_p(point c,double r,point l1,point l2,point &p1,point &p2)
{point p = c;double t;p.x += l1.y - l2.y;p.y += l2.x - l1.x;p = l2l_inst_p(p,c,l1,l2);t = sqrt(r*r - disp2p(p,c)*disp2p(p,c))/disp2p(l1,l2);p1.x = p.x + (l2.x - l1.x)*t;p1.y = p.y + (l2.y - l1.y)*t;p2.x = p.x - (l2.x - l1.x)*t;p2.y = p.y - (l2.y - l1.y)*t;
}
void c2c_inst_p(point c1,double r1,point c2,double r2,point &p1,point &p2)
{point u,v;double t;t = (1 + (r1*r1 - r2*r2)/disp2p(c1,c2)/disp2p(c1,c2))/2;u.x = c1.x + (c2.x - c1.x)*t;u.y = c1.y + (c2.y - c1.y)*t;v.x = u.x + c1.y - c2.y;v.y = u.y - c1.x + c2.x;l2c_inst_p(c1,r1,u,v,p1,p2);
}
bool c2c_tangent(point a,double r1,point b,double r2)
{if( dd(disp2p(a,b),r1+r2) || dd(disp2p(a,b),fabs(r1-r2)) )return true;return false;
}
point c2c_tangent_p(point a,double r1,point b,double r2)
{point t;if( dd(disp2p(a,b),r1 + r2)  ){t.x = (r1*b.x + r2*a.x)/(r1 + r2);t.y = (r1*b.y + r2*a.y)/(r1 + r2);return t;}t.x = (r1*b.x - r2*a.x)/(r1 - r2);t.y = (r1*b.y - r2*a.y)/(r1 - r2);return t;
}
int fugai[MAX];
double crossProduct(point a,point b,point c)//向量 ac 在 ab 的方向 顺时针是正 
{return (c.x - a.x)*(b.y - a.y) - (b.x - a.x)*(c.y - a.y);
}
double disp2l(point a,point l1,point l2)
{return fabs( crossProduct(a,l1,l2) )/disp2p(l1,l2);
}
bool onSegment(point a, point b, point c)
{if( dd(crossProduct(a,b,c),0.0) && dyd(c.x,min(a.x,b.x)) && xyd(c.x,max(a.x,b.x)) && dyd(c.y,min(a.y,b.y)) && xyd(c.y,max(a.y,b.y)) )return true;return false;
}bool xiangqie(point p, int n) {FOR(i, 0, n)if( !dd(disp2p(p, c[i]), d) )return false;return true;
}
//M在相交区域内 
bool Minall(point M, int n) {FOR(i, 0, n)if( dy(disp2p(M, c[i]), d) )return false;return true;
}
double solve(int n) {if( Minall(M, n) )return 0.0;int cnt = 0;double mmin = INF;//若最后求的点在圆弧上 FOR(i, 0, n) {if( xyd(disp2p(M, c[i]), d) )continue;point a, b;l2c_inst_p(c[i], d, M, c[i], a, b);double len = disp2p(c[i], M);if( dd(len, disp2p(a, M) + d) && Minall(a, n) && xy(len-d, mmin) )mmin = len-d;if( dd(len, disp2p(b, M) + d) && Minall(b, n) && xy(len-d, mmin) )mmin = len-d;}if( xy(mmin, INF) )return mmin;FOR(i, 0, n)FOR(k, i+1, n) {if( dy(disp2p(c[i], c[k]), 2*d) )return -1;if( dd(disp2p(c[i], c[k]), 2*d) ) {point p;p.x = (c[i].x + c[k].x)/2;p.y = (c[i].y + c[k].y)/2;if( xiangqie(p, n) )return disp2p(p, M);elsereturn -1;}if( c[i] == c[k] )continue;point a, b;c2c_inst_p(c[i], d, c[k], d, a, b);if( Minall(a, n) ) {double len = disp2p(M, a);if( xy(len, mmin) ) mmin = len;}if( Minall(b, n) ) {double len = disp2p(M, b);if( xy(len, mmin) )mmin = len;}}return mmin;
}
int main()
{int ncases, n, ind = 1;while( ~scanf("%lf%lf%lf", &M.x, &M.y, &d) ) {scanf("%d", &n);FOR(i, 0, n)c[i].get();double ans = solve(n);if( ans < 0 )printf("X\n");elseprintf("%.2lf\n", ans);}return 0;
}