POS

词性标注（Part-of-Speech Tagging，POS Tagging）是自然语言处理（NLP）中的一项基本任务，它的发展历史可以大致分为以下几个阶段：

• 规则和词典驱动的方法：在早期，词性标注主要依赖于手工编写的规则和词典。在这种方法中，会有一套详尽的规则用于确定词的词性，这些规则通常是由语言学家根据他们对语言的理解而制定的。同时，也会有一本包含了大量词语及其对应词性的词典供参考。这种方法的痛点在于需要大量的人力来编写规则和维护词典，而且规则的适用性可能会受到语言变化和地区差异的影响。

• 基于统计的方法：随着计算机技术的发展和大量文本数据的可用性，基于统计的方法开始被引入到词性标注中。这种方法使用标注过的语料库（corpus）来训练模型，通过学习每个词出现的频率和上下文来决定词性。这种方法中最常见的模型就是隐马尔科夫模型（Hidden Markov Model，HMM）。HMM 可以有效地处理词性标注的问题，因为它可以同时考虑到每个词的局部上下文和全局序列性。然而，HMM 仍然存在一些限制，比如它只能考虑到有限的上下文，并且对于稀有词和新词的处理能力较弱。

• 基于机器学习的方法：进一步发展，人们开始使用更复杂的机器学习模型，如决策树、最大熵模型、条件随机场（Conditional Random Fields，CRF）等来进行词性标注。这些模型能够考虑更丰富的特征，包括词本身的信息、词的上下文信息、以及词的其他语言特性等。但这些模型的训练和推理通常比 HMM 更复杂，需要更多的计算资源。

• 基于深度学习的方法：近年来，随着深度学习的发展，人们开始使用神经网络，特别是循环神经网络（RNN）和转换器（Transformer）等模型来进行词性标注。这些模型可以捕获长距离的依赖关系，处理复杂的语言结构，而且可以自动从数据中学习有效的特征，对于稀有词和新词的处理能力也有所提高。然而，深度学习方法通常需要大量的标注数据和计算资源，对于资源受限的语言或任务，这可能是一个问题。

隐马尔可夫模型

• 在这个 POS 的任务中，我们的目标是：给定一个 sentence w，我们对每个词生成一个标注 tag，这些 tag 构成了 tag 序列 t；在这个过程中我们希望选择能够使得 t 序列概率最大的结果
  

• 因此，我们假设概率最大的结果为 $\hat{t}$, 并且根据贝叶斯公式，我们可以得到 $$\hat{t}=\underset{t}{\mathrm{argmax}}\frac{P(w|t)P(t)}{P(w)}$$

• 又因为分母 $P(w)$ 本质上与 $t$ 无关，所以这个分母可以被忽略掉，不会影响计算结果，因此可以简化公式为：
  $$\hat{t}=\underset{t}{\mathrm{argmax}}P(w|t)P(t)$$

• 因为 $w$ 和 $t$ 表示的都是整个句子层面的，现在我们将整个公式拆解成每个单词和 tag 的概率的连乘，即：
  

• 这个过程中我们遵循两个强假设：

  • ① 当前的 tag 的概率只取决于上一个 tag $$P(t)=\prod _{i=1}^{n}P(t_i|t_{i-1})$$
  • ② 当前word的概率 只 取决于当前的 tag $$P(w|t)=\prod _{i=1}^{n}P(w_i|t_i)$$

• 举个更加直观的例子，假设我现在有一个句子 I like eating fish:

  • 当我们从左到右看第二个单词 like （这里之所以拿 like 举例是因为 i 比较特殊，但是后面会解释）的时候，它的概率只取决于 like 的词性 tag。这其实也比较合理，因为当我们说 “我喜欢吃鱼” 的时候，我们遵从的规则其实不是单词本身，而是不同词之间的词性关系，因为说了一个 动词（like），所以下一个词大概率就会说一个 名词 (eating)，这是核心思想。
  • 比如你已经说了 like，这是个 动词，那么下一个词我们根据 ① ，知道或许可以说个名词，那我们就从名词里面挑一个吧，或许可以挑到 eating，所以我们看： eating 这个 word 是因为我们已经知道了当前位置的词性 tag，所以我们第 ② 个假设 （当前word的概率 只 取决于当前的 tag） 也是合理的

• 以上就是 隐马尔科夫模型，它的两个特点决定了它为什么叫 隐马尔科夫假设：

  • 马尔科夫假设：做一个不严谨的总结就是：在一个序列模型中，某个时刻 $t$ 事件的概率，仅有 $t-1$ 时刻的事件决定，也就是原本应该写成 $$P(x_i|x_{i-1}{x}_{i-2}....)$$ 直接简化成 $P(x_i|x_{i-1})$
  • 隐变量：在隐马尔可夫模型中，“隐” 指的是我们想要推断的状态序列是不可观测的或者说是隐藏的。具体到词性标注任务中，“隐” 指的就是每个词的词性 tag。在词性标注任务中，我们可以观察到的是文本中的词语（观测序列），而我们想要推断的是这些词对应的词性（状态序列）。 举个例子来说：I like eating fish 还是在这句话中，当我们观察到 like，但是我们不知道 like 的词性是什么，可能有人要问了 Like 可以做 动词 啊，那 like 也可以做副词啊，所以这里其实我们需要推断 Like 的词性到底是什么， 因此词性对我们来说是要根据上下文进行推断的量，因此称为隐变量。

• 即，在这张图中，$P(w_i|t_i)$ 说明当前的 $w_i$ 只取决于 $t_i$ 这个隐变量；同时 $P(t_i|t_{i-1})$ 体现出了马尔科夫性质（只与前一个状态有关）

计算简介

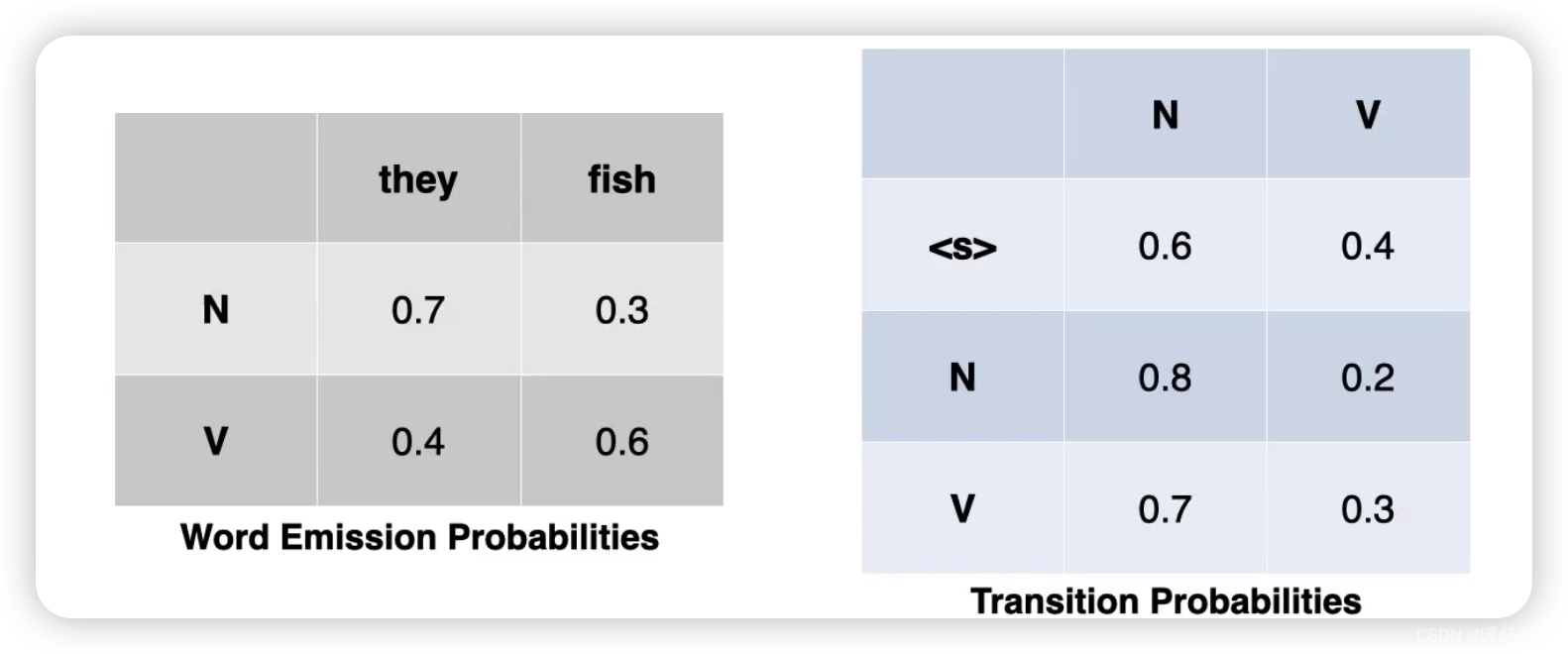
• 隐马尔科夫模型的计算基于两个概率 $P(t_i|t_{i-1})$ 和 $P(w_i|t_i)$，这两个概率都可以通过对数据集进行统计来轻松获得，例如上面图片中的 $P(like|VB)$ 和 $P(NN|DT)$

从 $P(t_i|t_{i-1})$ 我们不禁提问，对于一个 tag 应该如何处理呢：

• 我们默认第一个 tag 就是 $</s>$，然后按照相同的方式统计数量来获得概率（具体情况会在下面的实例中展示

那如果有的 (word, tag) 不存在怎么办？

• 采用平滑的方式解决

转移概率矩阵（Transition matrix）

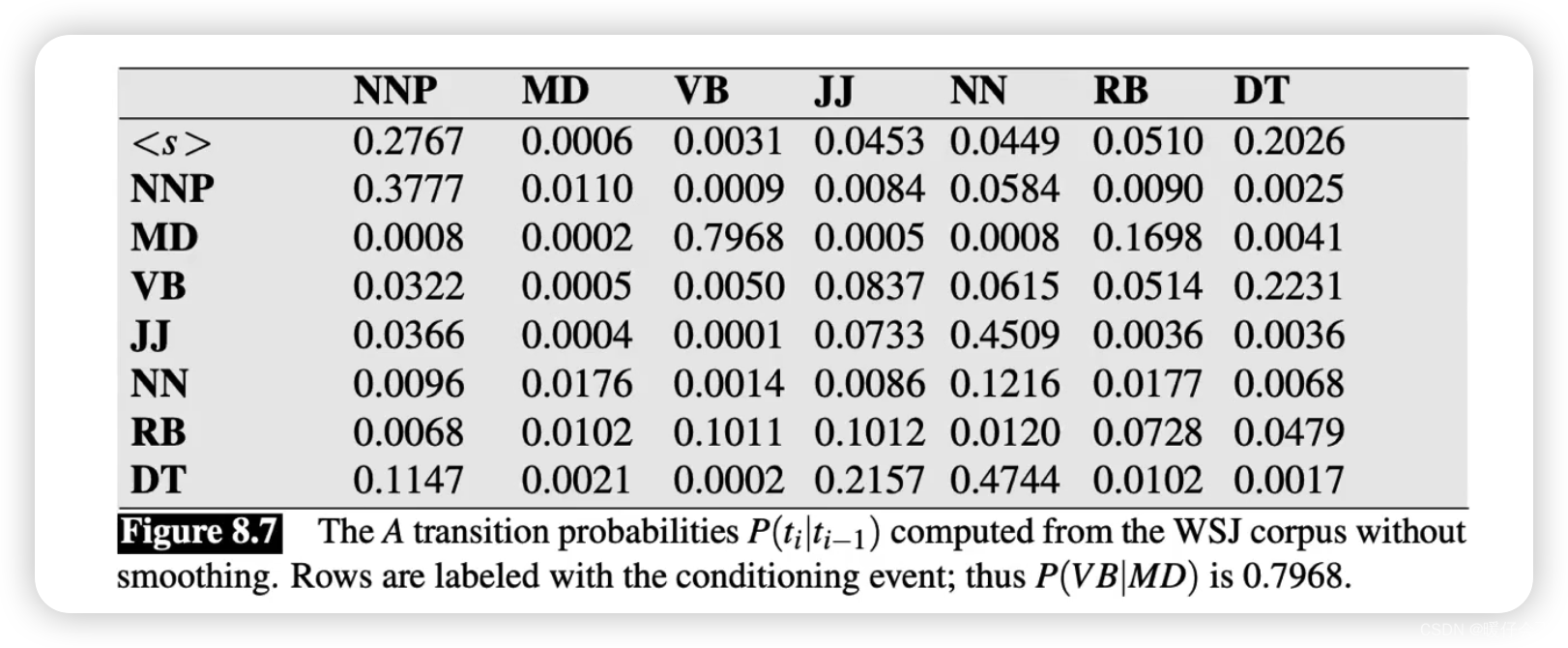
• 为了计算 $P(t_i|t_{i-1})$，我们可以先根据统计的方法得到 转移概率矩阵，然后采用查表的方式获得 $P(t_i)$ 和 $P(t_{i-1})$，表中的内容的阅读顺序应该是先看 row 再看 column，比如我要看 $P(NNP|MD)$ 也就是 在给定 MD 条件下 NNP 的概率 我们应该找到 MD 所在的行，然后去看 NNP 所在的列，最终得到 0.0008
  

观察矩阵（Observation / emission Matrix）

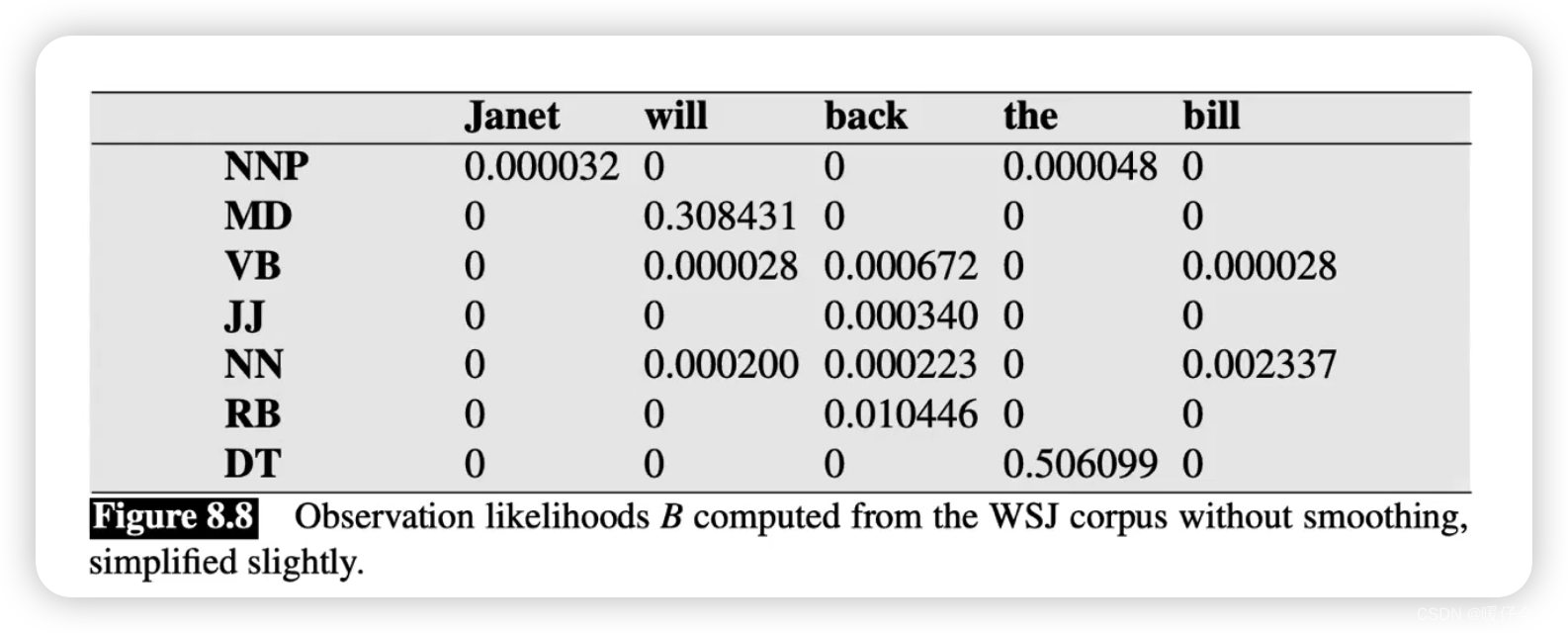
• 看这个表的方法和上一个表是完全一样的，当我们想得到 $P(janet|NNP)$ 即，给定 NNP 条件下 Janet 这个词出现的概率，则先找到 NNP 所在的行，然后找到 janet 所在的列，最终得到 0.000032

预测 prediction

• 一定要注意的一点是：我们需要求得的全局的最优解，而并非针对某一个时刻的最优概率，因此我们需要通过一个表格来计算每个步骤所得的概率，然后直到整个表格计算完成才能决定我们到底选择哪一种方案作为全局最优的解。我们将会在 Viterbi 算法中详解这个思想

Vitervi 算法

• 首先我们现在有什么：

  • 转移矩阵 $T$
    

  • 观察矩阵 $O$
    

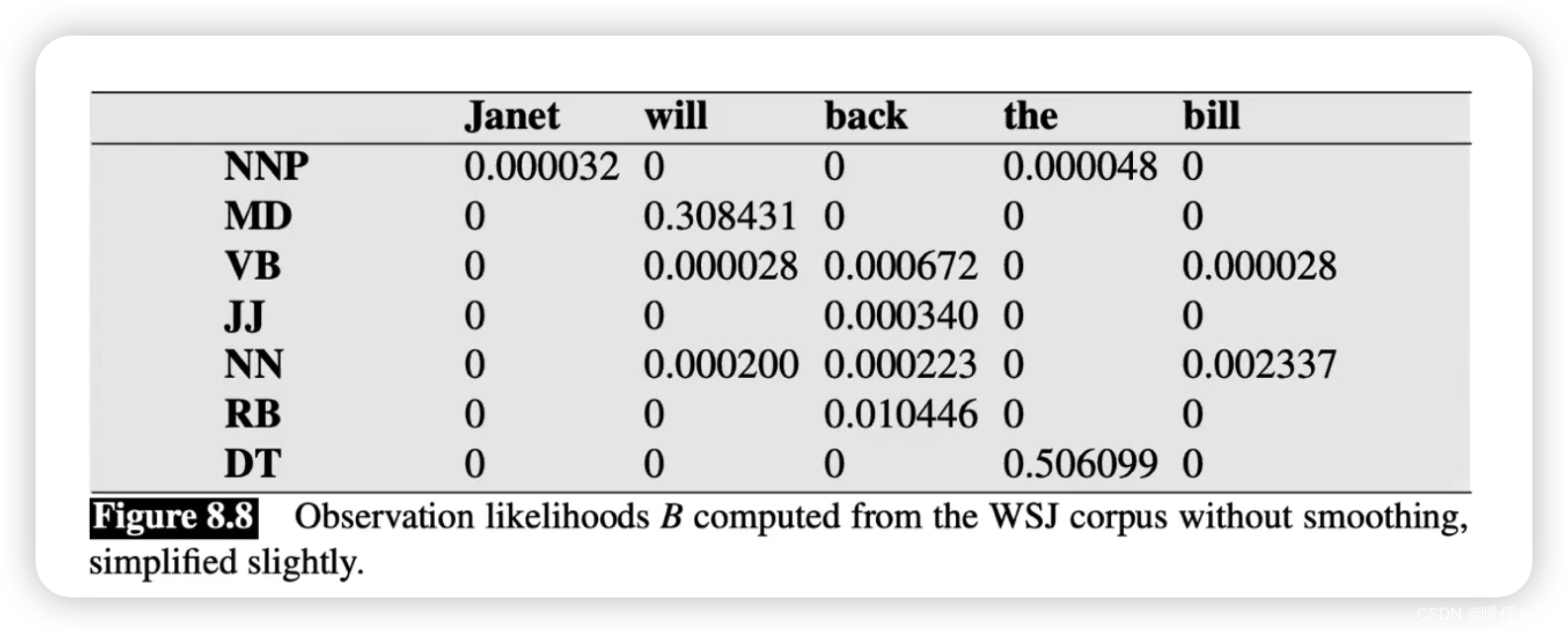
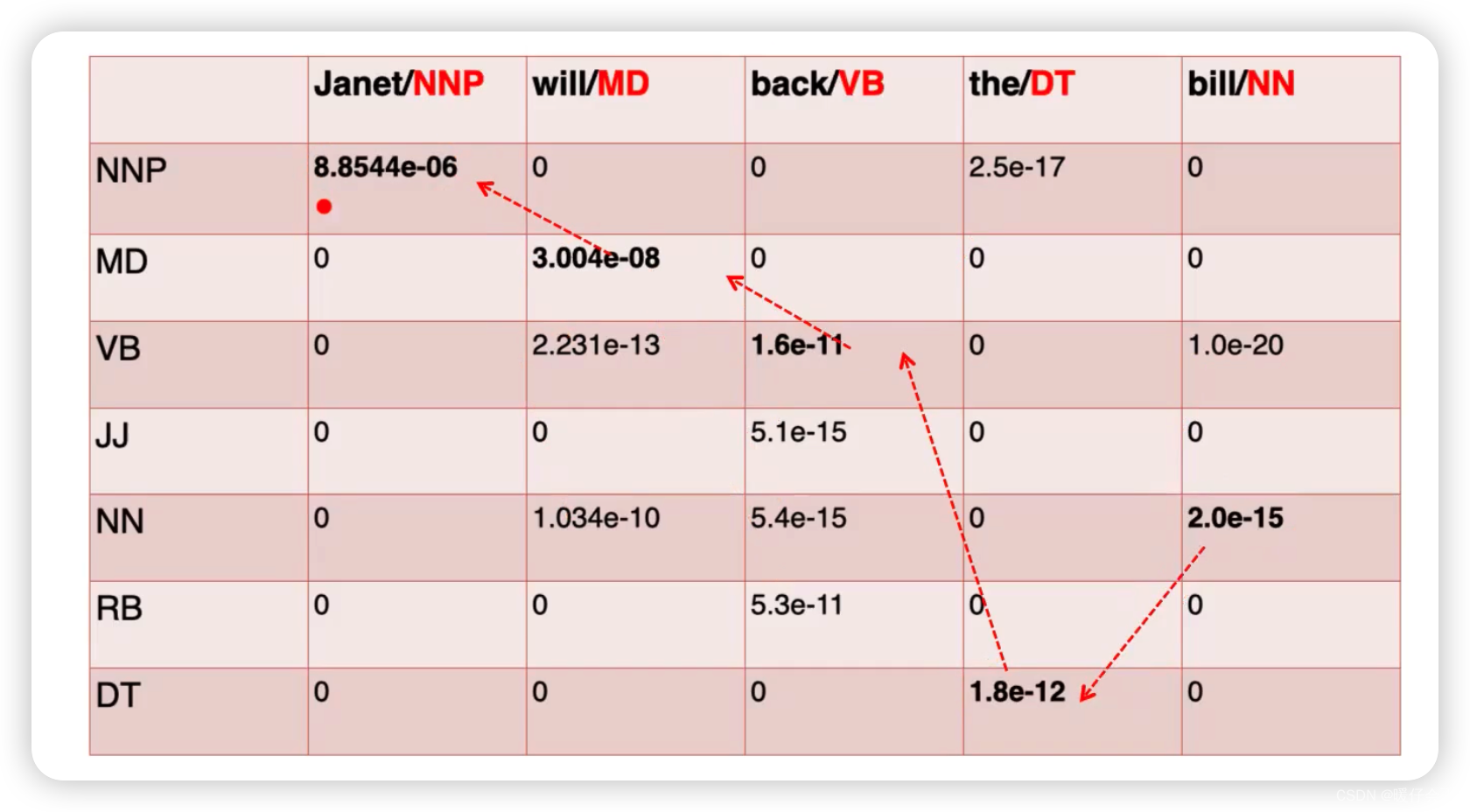
• 对于第一个格子：
  
  我们求算的概率是 $P(NNP|Janet)$，这里可能要有人有疑问了：

  之前不是说在读 Transition 和 观察矩阵 的时候说 “先读行，再读列”，那么按照这个原则，这里的概率应该表示的是 $P(Janet|NNP)$ 才对啊？

• 这里一定要注意，我们求算的这个表格的目的是，当我们有一个句子 Janet will back the bill 这句话，我们要对每个单词预测一个合理的 tag，并最终组成一个 tag 序列，这个 tag 序列的概率还要是所有可能的 tag 序列中最大的，

• 因此我们在求算的过程中，我们的已知一定是某个单词，例如 Janet，千万不要看到表格就觉的是一样的， 这个是求算过程的表格，跟 Transition 和 Observation 没啥关系

---

下面正式进入计算过程：

• 在第一个时刻 $\hat{t}$， $P(t_i|w_i)=P(NNP|Janet)=P(w_i|t_i)\ast P(t_i|t_{i-1})$

• 此时的 $w_i=Janet$, $t_i=NNP$， $t_{i-1}=</s>$ 所以直接带入：
  $$P(NNP|Janet)=P(Janet|NNP)\ast (NNP|</s>)=0.2767\ast 0.000032$$

• 直接查表：
  

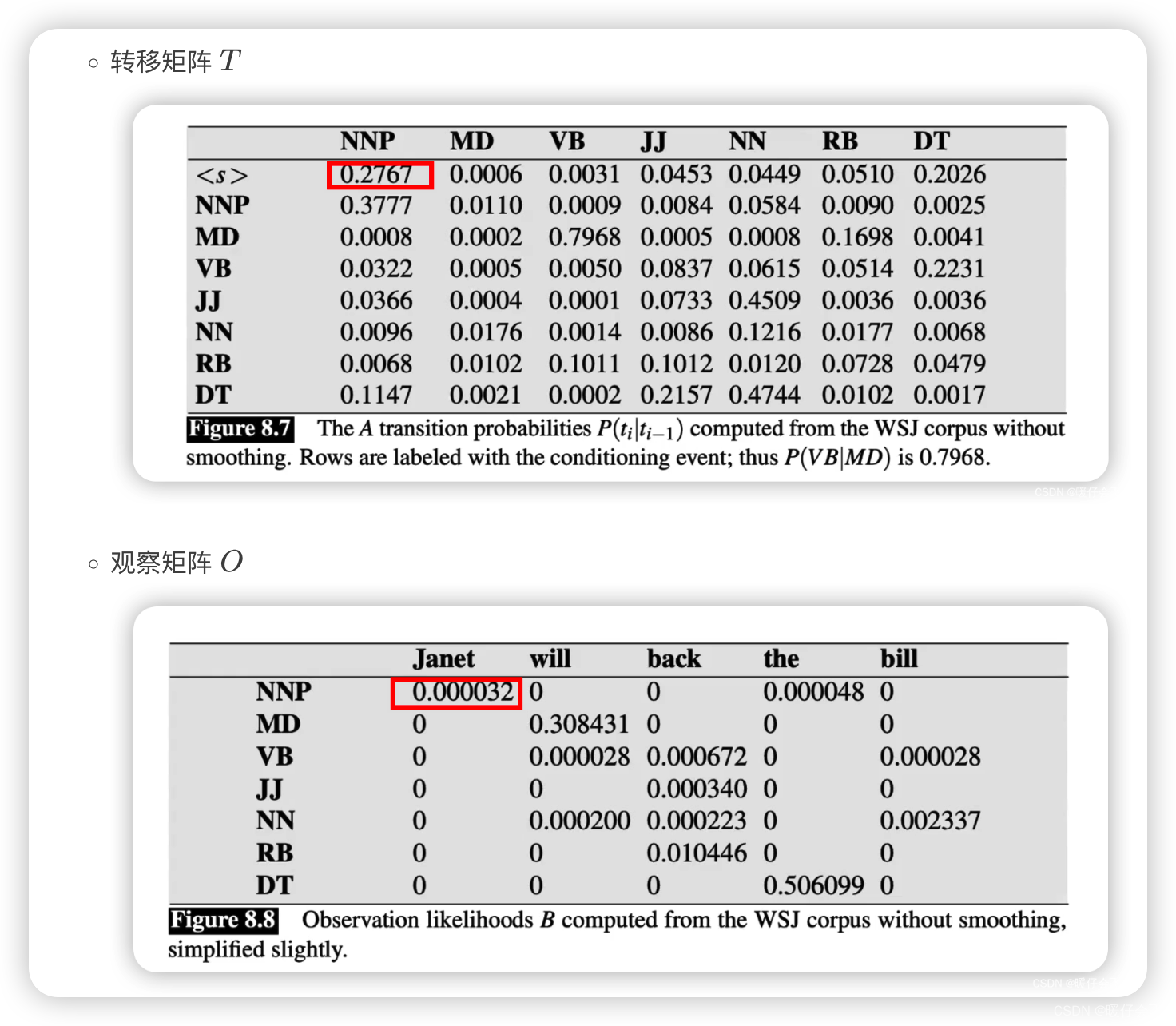
• 接下来是第一列的其他格子：

  • 由于给定 Janet，它的词性并不一定只有一种，因此要计算所有 Janet 可能的词性，计算方式都是一样的，可以得到一系列结果：
    $$P(NNP|Janet)=P(Janet|MD/VB/JJ/....)\ast (MD/VB/JJ/....|</s>)$$
  • 通过查 观察矩阵 可以发现 $P(Janet|MD/VB/JJ/....)$ 都是 0，因此这一列除了 $P(Janet|NNP)$ 之外，结果都是 0
    

---

• 现在来计算第二列
• 我们现在还不能确定 Janet 的词性就是 NNP 这是因为我们的这个序列还没算完，序列整体的概率还不能保证是全局最优的，因此我们要在当前第一列的基础上继续算下去。
• 当我们看到 will 的时候我们已经知道，第一个词是 Janet，并且给定 Janet 的所有词性 （NNP, MD, VB, ...）的概率
• 第二列我们重复上述过程，计算的是给定 will 这个词的条件下，所有词性的概率，我们还是从 NNP 这个词性开始：

$$P(NNP|will)=P(will|NNP)\ast \underline{P(NNP|t_{i-1})}$$

• 这里的 $t_{i-1}$ 需要考虑多种情况，因为在 will 之前是 Janet, 我们需要考虑 Janet 在各种词性下的取值。

• 所以我们在考虑 $P(NNP|will)$ 的时候，我们需要考虑 Janet 取所有可能情况中的最大值，即：
  P ( N N P ∣ w i l l ) = m a x { P ( w i l l ∣ N N P ) ∗ P ( N N P ∣ N N P ) ∗ P ( N N P ∣ J a n e t ) , P ( w i l l ∣ N N P ) ∗ P ( N N P ∣ M D ) ∗ P ( M D ∣ J a n e t ) , P ( w i l l ∣ N N P ) ∗ P ( N N P ∣ V B ) ∗ P ( V B ∣ J a n e t ) , . . . , P ( w i l l ∣ N N P ) ∗ P ( N N P ∣ D T ) ∗ P ( D T ∣ J a n e t ) , } P(NNP | will) =max\{ \\ P(will | NNP) *{P(NNP | NNP) * P(NNP|Janet)}, \\P(will | NNP) *{P(NNP | MD) * P(MD|Janet)}, \\P(will | NNP) *{P(NNP | VB) * P(VB|Janet)},\\ ..., \\P(will | NNP) *{P(NNP | DT) * P(DT|Janet)}, \\ \} P(NNP∣will)=max{P(will∣NNP)∗P(NNP∣NNP)∗P(NNP∣Janet),P(will∣NNP)∗P(NNP∣MD)∗P(MD∣Janet),P(will∣NNP)∗P(NNP∣VB)∗P(VB∣Janet),...,P(will∣NNP)∗P(NNP∣DT)∗P(DT∣Janet),}

• 对于 max 中的每一项，他们的最后一个部分都是我们在第一列中求出的值，例如：$P(NNP|Janet)=8.8544e^{-6}$，因此我们可以求出 $P(NNP|will)$ 取最大的值应该等于：
  $$P(NNP|will)=P(will|NNP)\ast P(NNP|NNP)\ast 8.8544e^{-6}$$

• 通过查表发现：$P(will|NNP)=0$ 因此 $P(NNP|will)=0\ast 0.3777\ast 8.8544e^{-6}=0$
  
  

• 同样的按照这个方法求算第二列中其他部分的值，每个格子进行计算的时候都要考虑到 Janet 所在列的计算结果。
  

• 同时在得到每一个格子中的最大值时，我们同样应该保留 track， 比如在当前例子中，如果 $P(MD|will)$ 最终取最大值的时候是因为 $P(MD|will)=P(will|MD)\ast P(MD|NNP)\ast P(NNP|Janet)$，那么他的上一个 tag 是 NNP，这个关系是需要被记录下来的，因为在最后一步计算完成后，我们会得到完整的 track，这个 track 会具有全局最优的概率：
  
  

练习