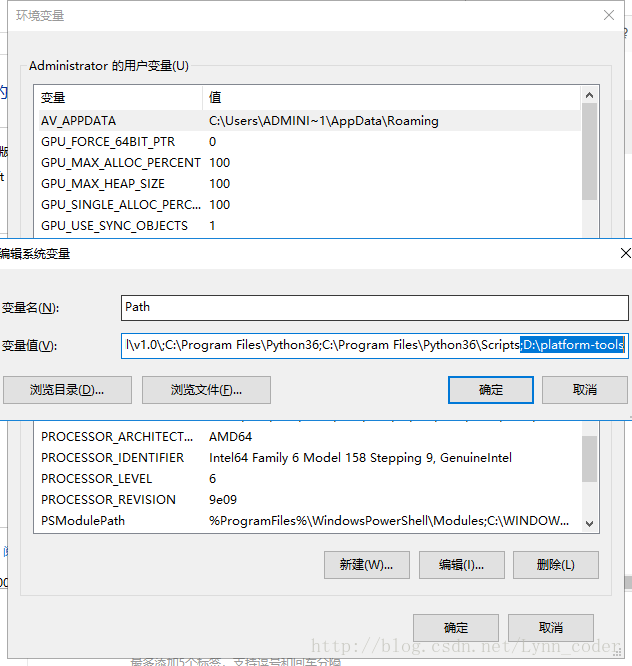
链接:
HDU : http://acm.hdu.edu.cn/showproblem.php?pid=2489
POJ : http://poj.org/problem?id=3925
题目:
Problem Description
For a tree, which nodes and edges are all weighted, the ratio of it is calculated according to the following equation.
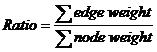
Given a complete graph of n nodes with all nodes and edges weighted, your task is to find a tree, which is a sub-graph of the original graph, with m nodes and whose ratio is the smallest among all the trees of m nodes in the graph.
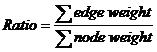
Given a complete graph of n nodes with all nodes and edges weighted, your task is to find a tree, which is a sub-graph of the original graph, with m nodes and whose ratio is the smallest among all the trees of m nodes in the graph.
Input
Input contains multiple test cases. The first line of each test case contains two integers n (2<=n<=15) and m (2<=m<=n), which stands for the number of nodes in the graph and the number of nodes in the minimal ratio tree. Two zeros end the input. The next line contains n numbers which stand for the weight of each node. The following n lines contain a diagonally symmetrical n×n connectivity matrix with each element shows the weight of the edge connecting one node with another. Of course, the diagonal will be all 0, since there is no edge connecting a node with itself.
All the weights of both nodes and edges (except for the ones on the diagonal of the matrix) are integers and in the range of [1, 100].
The figure below illustrates the first test case in sample input. Node 1 and Node 3 form the minimal ratio tree.
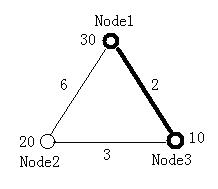
All the weights of both nodes and edges (except for the ones on the diagonal of the matrix) are integers and in the range of [1, 100].
The figure below illustrates the first test case in sample input. Node 1 and Node 3 form the minimal ratio tree.

Output
For each test case output one line contains a sequence of the m nodes which constructs the minimal ratio tree. Nodes should be arranged in ascending order. If there are several such sequences, pick the one which has the smallest node number; if there's a tie, look at the second smallest node number, etc. Please note that the nodes are numbered from 1 .
Sample Input
3 2 30 20 10 0 6 2 6 0 3 2 3 0 2 2 1 1 0 2 2 0 0 0
Sample Output
1 3 1 2
题目大意:
有一个n个点的图, 然后给出n*n的邻接矩阵图, 要求这个图的m个结点的子图,使得这个子图所有边之和与所有点之和的商值最小。
分析与总结:
直接dfs枚举出n个点所有的m个点的组合,然后对m个点求最小生成树,便可得出答案。
dfs枚举n个点的m个点组合,对于每个点,要么属于这个组合,要么是不属于,所以复杂度为2^n, n最大为15, 再加上减枝, 时间足足矣。
代码:
#include<cstdio>
#include<cstring>
#define N 20
int n,m,vis[N], ans[N], pre[N], hash[N];
double G[N][N], weight[N], minCost[N], minRatio;double prim(){memset(hash, 0, sizeof(hash));int u;for(int i=1; i<=n; ++i)if(vis[i]){u=i; break;}hash[u] = 1;double weightSum=0, edgeSum=0;for(int i=1; i<=n; ++i)if(vis[i]){minCost[i] = G[u][i]; pre[i] = u;weightSum += weight[i];}for(int i=1; i<m; ++i){u=-1;for(int j=1; j<=n; ++j)if(vis[j]&&!hash[j]){if(u==-1 || minCost[u]>minCost[j])u=j;}edgeSum += G[pre[u]][u];hash[u] = 1;for(int j=1; j<=n; ++j)if(vis[j]&&!hash[j]){if(minCost[j] > G[u][j]){minCost[j] = G[u][j];pre[j] = u;}}}return edgeSum/weightSum;
}void dfs(int u, int num){if(num>m) return; if(u==n+1){if(num!=m) return;double t=prim();if(t<minRatio){minRatio = t;memcpy(ans, vis, sizeof(vis));}return;}vis[u] = 1;dfs(u+1, num+1);vis[u] = 0;dfs(u+1, num);
}int main(){while(~scanf("%d%d",&n,&m)){if(!n&&!m) break; for(int i=1; i<=n; ++i) scanf("%lf",&weight[i]);for(int i=1; i<=n; ++i)for(int j=1; j<=n; ++j)scanf("%lf",&G[i][j]);memset(vis, 0, sizeof(vis));minRatio = 100000000;dfs(1, 0);bool flag=false;for(int i=1; i<=n; ++i)if(ans[i]){if(flag) printf(" %d", i);else { printf("%d",i); flag=true; }}puts("");}return 0;
—— 生命的意义,在于赋予它意义。