红黑树

特点：

1、红黑树不是一个平衡树
2.红黑树节点左右子树高度差长的不能超过短的二倍
牺牲了一些平衡，使得插入操作更快
3.红黑树插入做多旋转两次，删除最多旋转三次

五个性质：

1.每个节点都有颜色，不是红色，就是黑色
2.叶子结点（left和right）是黑色(null)
3.根节点root必须是黑色
4.不能出现连续的红色节点
5.从根节点root到达每一个叶子结点的路径上，黑色节点的路径都是相同的
在这里插入图片描述

插入：

树是空的，第一个插入的根节点是黑色。树不为空，新插入的节点为红色，然后检查父节点，父节点是黑色，插入完成；父节点是红色，进行红黑树的插入调整以下为插入调整的三种情况：
（为了更方便理解，用叔叔表示其父节点的兄弟节点，爷爷表示其父节点的父节点）
1.父节点是红色，叔叔节点也是红色
a.将父节点和叔叔节点颜色换成黑色
b.将爷爷节点颜色换成红色
c.指针指向爷爷节点
d.检查当前指向节点的父节点颜色是否为红色，如果为红色则重复这一操作，反之则插入成功
在这里插入图片描述
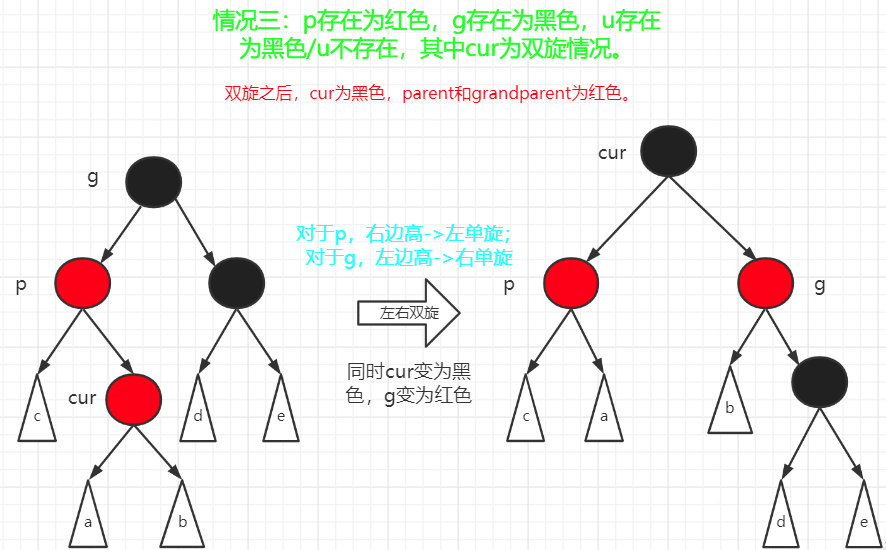
2.父节点颜色为红色，叔叔节点颜色为黑色，新节点节点，父节点以及爷爷节点在同一侧
a.将父节点颜色置为黑色
b.爷爷节点颜色置为红色
c.进行右旋或左旋操作（在根节点左边进行右旋操作，右边进行左旋操作）
在这里插入图片描述
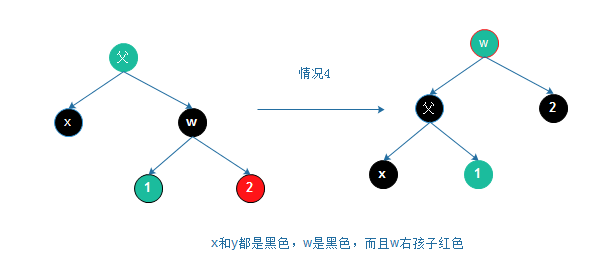
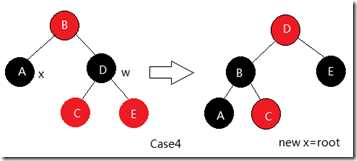
3.父节点颜色为红色，叔叔节点为黑色，新节点，父节点以及爷爷节点不在同一侧
a.对以父节点为根节点的这颗子树进行左旋或右旋操作，使当前节点，父节点，爷爷节点三者在同一侧
b.参照第二种情况，按顺序一步步执行
在这里插入图片描述 插入操作代码如下

 private void insert(T data){if (root==null){root=new RBNode<>(data,null,null,null,Color.BLACK);return;}RBNode<T> node=this.root;RBNode<T> parent=null;while (node!=null){parent=node;if (node.getData().compareTo(data)>0){node=node.getLeft();}else if (node.getData().compareTo(data)<0){node=node.getRight();}else {return;}}//判断应该插在叶子节点的哪边if (parent.getData().compareTo(data)>0){parent.setLeft(new RBNode<>(data,null,null,parent,Color.RED));}else if (parent.getData().compareTo(data)<0){parent.setRight(new RBNode<>(data,null,null,parent,Color.RED));}//如果新插入节点的父节点是红色，需要做插入调整if (color(parent(node))==Color.RED){fixAfterInsert(node);}}private void fixAfterInsert(RBNode<T> node) {while(color(parent(node)) == Color.RED){if(left(parent(parent(node))) == parent(node)){// 当前节点，父节点在祖先节点的左子树RBNode<T> uncle = right(parent(parent(node)));if(color(uncle) == Color.RED){ // 插入情况1setColor(parent(node), Color.BLACK);setColor(uncle, Color.BLACK);setColor(parent(parent(node)), Color.RED);node = parent(parent(node));} else {if(node == right(parent(node))){ // 插入情况3前半段node = parent(node);leftRotate(node);}setColor(parent(node), Color.BLACK); // 插入情况3后半段和情况2合并setColor(parent(parent(node)), Color.RED);rightRotate(parent(parent(node)));}} else {// 当前节点，父节点在祖先节点的右树RBNode<T> uncle = left(parent(parent(node)));if(color(uncle) == Color.RED){ // 插入情况1setColor(parent(node), Color.BLACK);setColor(uncle, Color.BLACK);setColor(parent(parent(node)), Color.RED);node = parent(parent(node));} else {if(node == left(parent(node))){ // 插入情况3前半段node = parent(node);rightRotate(node);}setColor(parent(node), Color.BLACK); // 插入情况3后半段和情况2合并setColor(parent(parent(node)), Color.RED);leftRotate(parent(parent(node)));break;}}}// 有可能向上回溯到根节点跳出，把根节点置成黑色setColor(this.root, Color.BLACK);}

左旋操作

在这里插入图片描述

   private void leftRotate(RBNode<T> node){RBNode<T> child = node.getRight();child.setParent(node.getParent());if(node.getParent() == null){this.root = child;} else {if(node.getParent().getLeft() == node){node.getParent().setLeft(child);} else {node.getParent().setRight(child);}}node.setRight(child.getLeft());if(child.getLeft() != null){child.getLeft().setParent(node);}child.setLeft(node);node.setParent(child);}

右旋操作
在这里插入图片描述

 private void rightRotate(RBNode<T> node){//先将节点的右孩子保存起来RBNode<T> child=node.getLeft();//通过右旋之后，child.setParent(node.getParent());}private Color color(RBNode<T> node){return node == null ? Color.BLACK : node.getColor();}public void setColor(RBNode<T> node, Color color){node.setColor(color);}public RBNode<T> left(RBNode<T> node){return node.getLeft();}public RBNode<T> right(RBNode<T> node){return node.getRight();}public RBNode<T> parent(RBNode<T> node){return node.getParent();}
}